Material data definition | |||||||||
|
| ||||||||
ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE
Material definitions
Any number of materials can be defined in an analysis. Each material definition can contain any number of material behaviors, as required, to specify the complete material behavior. For example, in a linear static stress analysis only elastic material behavior may be needed, while in a more complicated analysis several material behaviors may be required.
A name must be assigned to each material definition. This name allows the material to be referenced from the section definitions used to assign this material to regions in the model.
Input File Usage
MATERIAL, NAME=name
Each material definition is specified in a data block, which is initiated by a MATERIAL option. The material definition continues until an option that does not define a material behavior (such as another MATERIAL option) is introduced, at which point the material definition is assumed to be complete. The order of the material behavior options is not important. All material behavior options within the data block are assumed to define the same material.
Abaqus/CAE Usage
Property module: material editor: Name Use the menu bar under the Material Options list to add behaviors to a material.
![]()
Large-strain considerations
When giving material properties for finite-strain calculations, “stress” means “true” (Cauchy) stress (force per current area) and “strain” means logarithmic strain. For example, unless otherwise indicated, for uniaxial behavior
![]()
Specifying material data as functions of temperature and independent field variables
Material data are often specified as functions of independent variables such as temperature. Material properties are made temperature dependent by specifying them at several different temperatures.
In some cases a material property can be defined as a function of variables calculated by Abaqus; for example, to define a work-hardening curve, stress must be given as a function of equivalent plastic strain.
Material properties can also be dependent on “field variables” (user-defined variables that can represent any independent quantity and are defined at the nodes, as functions of time). For example, material moduli can be functions of weave density in a composite or of phase fraction in an alloy. See Specifying field variable dependence for details. The initial values of field variables are given as initial conditions (see Initial conditions in Abaqus/Standard and Abaqus/Explicit) and can be modified as functions of time during an analysis (see Predefined Fields). This capability is useful if, for example, material properties change with time because of irradiation or some other precalculated environmental effect.
Any material behaviors defined using a distribution in Abaqus/Standard (mass density, linear elastic behavior, and/or thermal expansion) cannot be defined with temperature and/or field dependence. However, material behaviors defined with distributions can be included in a material definition with other material behaviors that have temperature and/or field dependence. See Density, Linear elastic behavior, and Thermal expansion.
Interpolation of material data
In the simplest case of a constant property, only the constant value is entered. When the material data are functions of only one variable, the data must be given in order of increasing values of the independent variable. Abaqus then interpolates linearly for values between those given. The property is assumed to be constant outside the range of independent variables given (except for fabric materials, where it is extrapolated linearly outside the specified range using the slope at the last specified data point). Thus, you can give as many or as few input values as are necessary for the material model. If the material data depend on the independent variable in a strongly nonlinear manner, you must specify enough data points so that a linear interpolation captures the nonlinear behavior accurately.
When material properties depend on several variables, the variation of the properties with respect to the first variable must be given at fixed values of the other variables, in ascending values of the second variable, then of the third variable, and so on. The data must always be ordered so that the independent variables are given increasing values. This process ensures that the value of the material property is completely and uniquely defined at any values of the independent variables upon which the property depends. See Input Syntax Rules for further explanation and an example.
Example: Temperature-dependent linear isotropic elasticity
Figure 1 shows a simple, isotropic, linear elastic material, giving the Young's modulus and the Poisson's ratio as functions of temperature.
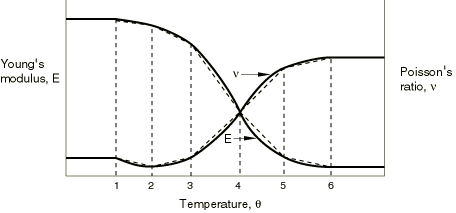
In this case six sets of values are used to specify the material description, as shown in the following table:
| Elastic Modulus | Poisson's Ratio | Temperature |
|---|---|---|
For temperatures that are outside the range defined by and , Abaqus assumes constant values for E and . The dotted lines on the graph represent the straight-line approximations that will be used for this model. In this example only one value of the thermal expansion coefficient is given, , and it is independent of temperature.
Example: Elastic-plastic material
Figure 2 shows an elastic-plastic material for which the yield stress is dependent on the equivalent plastic strain and temperature.

In this case the second independent variable (temperature) must be held constant, while the yield stress is described as a function of the first independent variable (equivalent plastic strain). Then, a higher value of temperature is chosen and the dependence on equivalent plastic strain is given at this temperature. This process, as shown in the following table, is repeated as often as necessary to describe the property variations in as much detail as required:
| Yield Stress | Equivalent Plastic Strain | Temperature |
|---|---|---|
Specifying field variable dependence
You can specify the number of user-defined field variable dependencies required for many material behaviors (see Predefined Fields). If you do not specify a number of field variable dependencies for a material behavior with which field variable dependence is available, the material data are assumed not to depend on field variables.
Input File Usage
*MATERIAL BEHAVIOR OPTION, DEPENDENCIES=n
*MATERIAL BEHAVIOR OPTION refers to any material behavior option for which field dependence can be specified. Each data line can hold up to eight data items. If more field variable dependencies are required than fit on a single data line, more data lines can be added. For example, a linear, isotropic elastic material can be defined as a function of temperature and seven field variables () as follows:
ELASTIC, TYPE=ISOTROPIC, DEPENDENCIES=7 E, , , , , , , ,
This pair of data lines would be repeated as often as necessary to define the material as a function of the temperature and field variables.
Abaqus/CAE Usage
Property module: material editor: material behavior: Number of field variables: n
material behavior refers to any material behavior for which field dependence can be specified.
![]()
Specifying material data as functions of solution-dependent variables
In Abaqus you can introduce dependence on solution variables with a user subroutine. User subroutines USDFLD in Abaqus/Standard and VUSDFLD in Abaqus/Explicit allow you to define field variables at a material point as functions of time, of material directions, and of any of the available material point quantities: those listed in Abaqus/Standard output variable identifiers for the case of USDFLD and those listed in Available output variable keys for the case of VUSDFLD. Material properties defined as functions of these field variables may, thus, be dependent on the solution.
User subroutines USDFLD and VUSDFLD are called at each material point for which the material definition includes a reference to the user subroutine.
For general analysis steps the values of variables provided in user subroutines USDFLD and VUSDFLD are those corresponding to the start of the increment. Hence, the solution dependence introduced in this way is explicit: the material properties for a given increment are not influenced by the results obtained during the increment. Consequently, the accuracy of the results will generally depend on the time increment size. This is usually not a concern in Abaqus/Explicit because the stable time increment is usually sufficiently small to ensure good accuracy. In Abaqus/Standard you can control the time increment from inside subroutine USDFLD. For linear perturbation steps the solution variables in the base state are available. (See General and perturbation procedures for a discussion of general and linear perturbation steps.)
Input File Usage
USER DEFINED FIELD
![]()
Defining the characteristic element length at a material point in Abaqus/Explicit
The characteristic element length is used by Abaqus for the regularization of models that exhibit strain softening or is passed to user subroutines that are called at a material point. By default, Abaqus computes the characteristic element length using the geometric mean–based definition.
The default value for a first-order element is the typical length of a line across an element, and the default value for a second-order element is half of the same typical length. For trusses the default value is a characteristic length along the element axis. For membranes and shells the default value is a characteristic length in the reference surface. For axisymmetric elements the default value is a characteristic length in the r–z plane only.
In Abaqus/Explicit you can redefine the value of the characteristic element length based on the element topology and geometry in user subroutine VUCHARLENGTH.
Input File Usage
Use the following option for the geometric mean–based definition of the characteristic element length (default):
CHARACTERISTIC LENGTH, DEFINITION=GEOMETRIC MEAN
Use the following option to specify the characteristic element length in user subroutine VUCHARLENGTH:
CHARACTERISTIC LENGTH, DEFINITION=USER, COMPONENTS=n, PROPERTIES=n
Abaqus/CAE Usage
User subroutine VUCHARLENGTH is not supported in Abaqus/CAE.
![]()
Regularizing user-defined data in Abaqus/Explicit
Interpolating material data as functions of independent variables requires table lookups of the material data values during the analysis. The table lookups occur frequently in Abaqus/Explicit and are most economical if the interpolation is from regular intervals of the independent variables. For example, the data shown in Figure 1 are not regular because the intervals in temperature (the independent variable) between adjacent data points vary. You are not required to specify regular material data. Abaqus/Explicit will automatically regularize user-defined data. For example, the temperature values in Figure 1 may be defined at 10°, 20°, 25°, 28°, 30°, and 35° C. In this case Abaqus/Explicit can regularize the data by defining the data over 25 increments of 1° C and your piecewise linear data will be reproduced exactly. This regularization requires the expansion of your data from values at 6 temperature points to values at 26 temperature points. This example is a case where a simple regularization can reproduce your data exactly.
If there are multiple independent variables, the concept of regular data also requires that the minimum and maximum values (the range) be constant for each independent variable while specifying the other independent variables. The material definition in Figure 2 illustrates a case where the material data are not regular since , , and . Abaqus/Explicit will also regularize data involving multiple independent variables, although the data provided must satisfy the rules specified in Input Syntax Rules.
Error tolerance used in regularizing user-defined data
It is not always desirable to regularize the input data so that they are reproduced exactly in a piecewise linear manner. Suppose the yield stress is defined as a function of plastic strain in Abaqus/Explicit as follows:
| Yield Stress | Plastic Strain |
|---|---|
| 50000 | .0 |
| 75000 | .001 |
| 80000 | .003 |
| 85000 | .010 |
| 86000 | 1.0 |
It is possible to regularize the data exactly but it is not very economical, since it requires the subdivision of the data into 1000 regular intervals. Regularization is more difficult if the smallest interval you defined is small compared to the range of the independent variable.
Abaqus/Explicit uses an error tolerance to regularize the input data. The number of intervals in the range of each independent variable is chosen such that the error between the piecewise linear regularized data and each of your defined points is less than the tolerance times the range of the dependent variable. In some cases the number of intervals becomes excessive and Abaqus/Explicit cannot regularize the data using a reasonable number of intervals. The number of intervals considered reasonable depends on the number of intervals you define. If you defined 50 or less intervals, the maximum number of intervals used by Abaqus/Explicit for regularization is equal to 100 times the number of user-defined intervals. If you defined more than 50 intervals, the maximum number of intervals used for regularization is equal to 5000 plus 10 times the number of user-defined intervals above 50. If the number of intervals becomes excessive, the program stops during the data checking phase and issues an error message. You can either redefine the material data or change the tolerance value. The default tolerance is 0.03.
The yield stress data in the example above are a typical case where such an error message may be issued. In this case you can simply remove the last data point since it produces only a small difference in the ultimate yield value.
Input File Usage
MATERIAL, RTOL=tolerance
Abaqus/CAE Usage
Property module: material editor: : Rtol: tolerance
Regularization of strain-rate-dependent data in Abaqus/Explicit
Since strain rate dependence of data is usually measured at logarithmic intervals, Abaqus/Explicit regularizes strain rate data using logarithmic intervals rather than uniformly spaced intervals by default. This will generally provide a better match to typical strain-rate-dependent curves. You can specify linear strain rate regularization to use uniform intervals for regularization of strain rate data. The use of linear strain rate regularization affects only the regularization of strain rate as an independent variable and is relevant only if one of the following behaviors is used to define the material data:
-
low-density foams (Low-density foams)
-
rate-dependent metal plasticity (Classical metal plasticity)
-
rate-dependent viscoplasticity defined by yield stress ratios (Rate-dependent yield)
-
shear failure defined using direct tabular data (Dynamic failure models)
-
rate-dependent Drucker-Prager hardening (Extended Drucker-Prager models)
-
rate-dependent concrete damaged plasticity (Concrete damaged plasticity)
-
rate-dependent damage initiation criterion (Damage initiation for ductile metals)
Input File Usage
Use the following option to specify logarithmic regularization (default):
MATERIAL, STRAIN RATE REGULARIZATION=LOGARITHMIC
Use the following option to specify linear regularization:
MATERIAL, STRAIN RATE REGULARIZATION=LINEAR
Abaqus/CAE Usage
Property module: material editor: : Strain rate regularization: Logarithmic or Linear
![]()
Evaluation of strain-rate-dependent data in Abaqus/Explicit
Rate-sensitive material constitutive behavior may introduce nonphysical high-frequency oscillations in an explicit dynamic analysis. To overcome this problem, Abaqus/Explicit computes the equivalent plastic strain rate used for the evaluation of strain-rate-dependent data as
Here is the incremental change in equivalent plastic strain during the time increment , and and are the strain rates at the beginning and end of the increment, respectively. The factor () facilitates filtering high-frequency oscillations associated with strain-rate-dependent material behavior. You can specify the value of the strain rate factor, , directly. The default value is 0.9. A value of does not provide the desired filtering effect and should be avoided.
Input File Usage
MATERIAL, SRATE FACTOR=
Abaqus/CAE Usage
You cannot specify the value of the strain rate factor in Abaqus/CAE.