Thermal expansion | |||||||||||
|
| ||||||||||
ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE
Defining thermal expansion coefficients
Thermal expansion is a material property included in a material definition (see Material data definition) except when it refers to the expansion of a gasket whose material properties are not defined as part of a material definition. In that case expansion must be used in conjunction with the gasket behavior definition (see Defining the gasket behavior directly using a gasket behavior model).
In an Abaqus/Standard analysis a spatially varying thermal expansion can be defined for homogeneous solid continuum elements by using a distribution (Distribution definition). The distribution must include default values for the thermal expansion. If a distribution is used, no dependencies on temperature and/or field variables for the thermal expansion can be defined.
Input File Usage
Use the following options to define thermal expansion for most materials:
MATERIAL EXPANSION
Use the following options to define thermal expansion for gaskets whose constitutive response is defined directly as gasket behavior:
GASKET BEHAVIOR EXPANSION
Abaqus/CAE Usage
Use the following option in conjunction with other material behaviors, including gasket behavior, to include thermal expansion effects:
Property module: material editor: Computation of thermal strains
Abaqus requires thermal expansion coefficients, , that define the total thermal expansion from a reference temperature, , as shown in Figure 1.
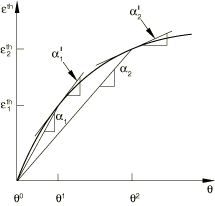
They generate thermal strains according to the formula
where
-
is the thermal expansion coefficient;
-
is the current temperature;
-
is the initial temperature;
-
are the current values of the predefined field variables;
-
are the initial values of the field variables; and
-
is the reference temperature for the thermal expansion coefficient.
The second term in the above equation represents the strain due to the difference between the initial temperature, , and the reference temperature, . This term is necessary to enforce the assumption that there is no initial thermal strain for cases in which the reference temperature does not equal the initial temperature.
Defining the reference temperature
If the coefficient of thermal expansion, , is not a function of temperature or field variables, the value of the reference temperature, , is not needed. If is a function of temperature or field variables, you can define .
Input File Usage
EXPANSION, ZERO=
Abaqus/CAE Usage
Property module: material editor: : Reference temperature:
Converting thermal expansion coefficients from differential form to total form
Total thermal expansion coefficients are commonly available in tables of material properties. However, sometimes you are given thermal expansion data in differential form:
that is, the tangent to the strain-temperature curve is provided (see Figure 1). To convert to the total thermal expansion form required by Abaqus, this relationship must be integrated from a suitably chosen reference temperature, :
For example, suppose is a series of constant values: between and ; between and ; between and ; etc. Then,
The corresponding total expansion coefficients required by Abaqus are then obtained as
![]()
Defining increments of thermal strain in user subroutines
Increments of thermal strain can be specified in user subroutine UEXPAN in Abaqus/Standard and in user subroutine VUEXPAN in Abaqus/Explicit as functions of temperature and/or predefined field variables. User subroutine UEXPAN in Abaqus/Standard must be used if the thermal strain increments depend on state variables.
Input File Usage
EXPANSION, USER
Abaqus/CAE Usage
Property module: material editor: : Use user subroutine UEXPAN
![]()
Defining the initial temperature and field variable values
If the coefficient of thermal expansion, , is a function of temperature or field variables, the initial temperature and initial field variable values, and , are given as described in Initial conditions in Abaqus/Standard and Abaqus/Explicit.
Element removal and reactivation
If an element has been removed and subsequently reactivated in Abaqus/Standard (Element and contact pair removal and reactivation), and in the equation for the thermal strains represent temperature and field variable values as they were at the moment of reactivation.
![]()
Defining directionally dependent thermal expansion
Isotropic or orthotropic thermal expansion can be defined in Abaqus. In addition, fully anisotropic thermal expansion can be defined in Abaqus/Standard. In Abaqus/Explicit fully anisotropic user thermal expansion can be defined in user subroutine VUEXPAN for plasticity material models.
Orthotropic and anisotropic thermal expansion can be used only with materials where the material directions are defined with local orientations (see Orientations).
Orthotropic thermal expansion in Abaqus/Explicit is allowed only with anisotropic elasticity (including orthotropic elasticity), anisotropic yield (see Anisotropic yield/creep), and user subroutine VUEXPAN.
Isotropic expansion
If the thermal expansion coefficient is defined directly, only one value of is needed at each temperature. If user subroutine UEXPAN is used, only one isotropic thermal strain increment () must be defined.
Input File Usage
Use the following option to define the thermal expansion coefficient directly:
EXPANSION, TYPE=ISO
Use the following option to define the thermal expansion with user subroutine UEXPAN in Abaqus/Standard and VUEXPAN in Abaqus/Explicit:
EXPANSION, TYPE=ISO, USER
Abaqus/CAE Usage
Use the following input to define the thermal expansion coefficient directly:
Property module: material editor: : Type: Isotropic
Use the following input to define the thermal expansion with user subroutine UEXPAN:
Property module: material editor: : Type: Isotropic, Use user subroutine UEXPAN
Orthotropic expansion
If the thermal expansion coefficients are defined directly, the three expansion coefficients in the principal material directions (, , and ) should be given as functions of temperature. If user subroutines UEXPAN and VUEXPAN are used, the three components of thermal strain increment in the principal material directions (, , and ) must be defined.
Input File Usage
Use the following option to define the thermal expansion coefficient directly:
EXPANSION, TYPE=ORTHO
Use the following option to define the thermal expansion with user subroutine UEXPAN in Abaqus/Standard and VUEXPAN in Abaqus/Explicit:
EXPANSION, TYPE=ORTHO, USER
Abaqus/CAE Usage
Use the following input to define the thermal expansion coefficient directly:
Property module: material editor: : Type: Orthotropic
Use the following input to define the thermal expansion with user subroutine UEXPAN:
Property module: material editor: : Type: Orthotropic, Use user subroutine UEXPAN
Anisotropic expansion
If the thermal expansion coefficients are defined directly, all six components of (, , , , , ) must be given as functions of temperature. If user subroutine UEXPAN is used in Abaqus/Standard, all six components of the thermal strain increment (, , , , , ) must be defined. If user subroutine VUEXPAN is used in Abaqus/Explicit, all six components of the thermal strain increment (, , , , ,) must be defined.
In an Abaqus/Standard analysis if a distribution is used to define the thermal expansion, the number of expansion coefficients given for each element in the distribution, which is determined by the associated distribution table (Distribution definition), must be consistent with the level of anisotropy specified for the expansion behavior. For example, if orthotropic behavior is specified, three expansion coefficients must be defined for each element in the distribution.
Input File Usage
Use the following option to define the thermal expansion coefficient directly:
EXPANSION, TYPE=ANISO
Use the following option to define the thermal expansion with user subroutine UEXPAN in Abaqus/Standard and VUEXPAN in Abaqus/Explicit:
EXPANSION, TYPE=ANISO, USER
Abaqus/CAE Usage
Use the following input to define the thermal expansion coefficient directly:
Property module: material editor: : Type: Anisotropic
Use the following input to define the thermal expansion with user subroutine UEXPAN:
Property module: material editor: : Type: Anisotropic, Use user subroutine UEXPAN
![]()
Thermal stress
When a structure is not free to expand, a change in temperature will cause stress. For example, consider a single two-node truss of length L that is completely restrained at both ends. The cross-sectional area; the Young's modulus, E; and the thermal expansion coefficient, , are all constant. The stress in this one-dimensional problem can then be calculated from Hooke's Law as , where is the total strain and is the thermal strain, where is the temperature change. Since the element is fully restrained, . If the temperature at both nodes is the same, we obtain the stress .
Constrained thermal expansion can cause significant stress. For typical structural metals, temperature changes of about 150°C (300°F) can cause yield. Therefore, it is often important to define boundary conditions with particular care for problems involving thermal loading to avoid overconstraining the thermal expansion.
Energy balance considerations
Abaqus does not account for thermal expansion effects in the total energy balance equation, which can lead to an apparent imbalance of the total energy of the model. For example, in the example above of a two-node truss restrained at both ends, constrained thermal expansion introduces strain energy that will result in an equivalent increase in the total energy of the model.
![]()
Material options
Thermal expansion can be combined with any other (mechanical) material (see Combining material behaviors) behavior in Abaqus.
Using thermal expansion with other material models
For most materials thermal expansion is defined by a single coefficient or set of orthotropic or anisotropic coefficients or, in Abaqus/Standard, by defining the incremental thermal strains in user subroutine UEXPAN. For porous media in Abaqus/Standard, such as soils or rock, thermal expansion can be defined for the solid grains and for the permeating fluid (when using the coupled pore fluid diffusion/stress procedure—see Coupled pore fluid diffusion and stress analysis). In such a case the thermal expansion definition should be repeated to define the different thermal expansion effects.
Using thermal expansion with gasket behaviors
Thermal expansion can be used in conjunction with any gasket behavior definition. Thermal expansion will affect the expansion of the gasket in the membrane direction and/or the expansion in the gasket's thickness direction.
![]()
Elements
Thermal expansion can be used with any stress/displacement or fluid element in Abaqus.