Using a general shell section to define the section behavior

A general shell section can be defined as follows:

• The section response can be specified by associating the section with a material definition or, in the case of a composite shell, with several different material definitions.

• The section properties can be specified directly.

• In Abaqus/Standard the section response can be programmed in user subroutine UGENS.

You can define the shell section's mechanical response by specifying the thickness; the material reference; and the orientation of the section or, for a composite shell, the orientation of each of its layers. Abaqus will determine the equivalent section properties. You must associate the section behavior with a region of your model.

The linear elastic material behavior is defined with a material definition (Material data definition), which may contain linear elastic behavior (Linear elastic behavior) and thermal expansion behavior (Thermal expansion). The density (Density) and damping (Material damping) behavior can also be specified as described below; in Abaqus/Explicit the density of the material must be defined. However, no nonlinear material properties, such as plastic behavior, can be included since Abaqus will precompute the section response and will not update that response during the analysis. Dependence of the linear elastic material behavior on temperature or predefined field variables is not allowed.

The shell section response is defined by

No temperature-dependent scaling of the modulus is included. The section forces and moments caused by thermal strains, $\left\{{\mathbf{N}}^{\mathbf{th}}\right\}$, vary linearly with temperature and are defined by

where $\left\{\overline{\mathbf{F}}\right\}$ are the generalized stresses caused by a fully constrained unit temperature rise that result from the user-defined thermal expansion, $\theta$ is the temperature, and ${\theta }^I$ is the initial (stress-free) temperature at this point in the shell (defined by the initial nodal temperatures given as initial conditions; see Defining initial temperatures).

You can define the section's mechanical response by specifying the general section stiffness and thermal expansion response—$\left[\mathbf{D}\right]$, $\left\{\mathbf{F}\right\}$, $Y\left(\theta ,f_{\beta }\right)$ and $\alpha \left(\theta ,f_{\beta }\right)$, as defined below—directly. Since this method then provides the complete specification of the section's mechanical response, no material reference is needed. Optionally, you can define ${\theta }^0$, the reference temperature for thermal expansion.

You must associate this section behavior with a region of your model.

In this case the shell section response is defined by

where

$\left\{\mathbf{N}\right\}$

are the forces and moments on the shell section (membrane forces per unit length, bending moments per unit length);

$\left\{\mathbf{E}\right\}$

are the generalized section strains in the shell (reference surface strains and curvatures);

$\left[\mathbf{D}\right]$

is the section stiffness matrix;

$Y\left(\theta ,f_{\beta }\right)$

is a scaling modulus, which can be used to introduce temperature $\left(\theta \right)$ and field-variable $\left(f_{\beta }\right)$ dependence of the cross-section stiffness; and

$\left\{{\mathbf{N}}^{\mathbf{th}}\right\}$

are the section forces and moments (per unit length) caused by thermal strains.

These thermal forces and moments in the shell are generated according to the formula

where

$\alpha \left(\theta ,f_{\beta }\right)$

is a scaling factor (the “thermal expansion coefficient”);

${\theta }^I$

is the initial (stress-free) temperature at this point in the shell, defined by the initial nodal temperatures given as initial conditions (Defining initial temperatures); and

$\left\{\mathbf{F}\right\}$

are the user-specified generalized section forces and moments (per unit length) caused by a fully constrained unit temperature rise.

If the coefficient of thermal expansion, $\alpha$, is not a function of temperature, the value of ${\theta }^0$ is not needed. Note the distinction between ${\theta }^0$, the reference value used in defining $\alpha$, and the stress-free initial temperature, ${\theta }^I$.

In these equations the order of the terms is

that is, the direct membrane terms come first, then the shear membrane term, then the direct and shear bending terms, with six terms in all. Engineering measures of shear membrane strain (${\gamma }_{12}$) and twist (${\kappa }_{12}$) are used in Abaqus.

This method of defining the shell section properties cannot be used with variable thickness shells or continuum shell elements.

See Laminated composite shells: buckling of a cylindrical panel with a circular hole for more information.

The stiffness matrix, $\left[\mathbf{D}\right]$, can be defined as a constant stiffness for the section or as a spatially varying stiffness by referring to a distribution (Distribution definition). If a spatially varying stiffness is used, the distribution must have a default stiffness defined. The default stiffness is used by any shell element assigned to the shell section that is not specifically assigned a value in the distribution.

SHELL GENERAL SECTION, ELSET=name, ZERO=${\theta }^0$

Property module:
Create Section: select Shell as the section Category and General shell stiffness as the section Type
AssignSection: select regions

In Abaqus/Standard you can define the section response in user subroutine UGENS for the more general case where the section response may be nonlinear. User subroutine UGENS is particularly useful if the nonlinear behavior of the section involves geometric as well as material nonlinearity, such as may occur due to section collapse. If only nonlinear material behavior is present, it is simpler to use a shell section integrated during the analysis with the appropriate nonlinear material model.

You must specify a constant section thickness as part of the section definition or a continuously varying thickness by defining the thickness at the nodes as described below. Even though the section's mechanical behavior is defined in user subroutine UGENS, the thickness of the shell section is required for calculation of the hourglass control stiffness. You must associate this section behavior with a region of your model.

Abaqus/Standard calls user subroutine UGENS for each integration point at each iteration of every increment. The subroutine provides the section state at the start of the increment (section forces and moments, $\mathbf{N}$; generalized section strains, $\mathbf{E}$; solution-dependent state variables; temperature; and any predefined field variables); the increments in temperature and predefined field variables; the generalized section strain increments, $\mathrm{△}\mathbf{E}$; and the time increment.

The subroutine must perform two functions: it must update the forces, the moments, and the solution-dependent state variables to their values at the end of the increment; and it must provide the section stiffness matrix, $\partial \mathbf{N}/\partial \mathbf{E}$. The complete section response, including the thermal expansion effects, must be programmed in the user subroutine.

You should ensure that the strain increment is not used or changed in user subroutine UGENS for linear perturbation analyses. For this case the quantity is undefined.

This method of defining the shell section properties cannot be used with continuum shell elements.

SHELL GENERAL SECTION, ELSET=name, USER

Idealizations allow you to modify the stiffness coefficients in a shell section based on assumptions about the shell's makeup or expected behavior. The following idealizations are available for general shell sections:

• Retain only the membrane stiffness for shells whose predominant response will be in-plane stretching.

• Retain only the bending stiffness for shells whose predominant response will be pure bending.

• Ignore the effects of the material layer stacking sequence for composite shells.

The membrane stiffness and bending stiffness idealizations can be applied to homogeneous shell sections, composite shell sections, or shell sections with the stiffness coefficients specified directly. The idealization to ignore stacking effects can be applied only to composite shell sections.

Idealizations modify the shell general stiffness coefficients after they have been computed normally, including the effects of offset.

• If you use any idealization, all membrane-bending coupling terms are set to zero.

• If you retain only the membrane stiffness, off-diagonal terms of the bending submatrix are set to zero, and diagonal bending terms are set to 1 × 10⁻⁶ times the largest diagonal membrane coefficient.

• If you retain only the bending stiffness, off-diagonal terms of the membrane submatrix are set to zero, and diagonal membrane terms are set to 1 × 10⁻⁶ times the largest diagonal bending coefficient.

• If you ignore the material layer stacking sequence in a composite shell, each term of the bending submatrix is set equal to T²/12 times the corresponding membrane submatrix term, where T is the total thickness of the shell.

SHELL GENERAL SECTION, MEMBRANE ONLY

SHELL GENERAL SECTION, BENDING ONLY

SHELL GENERAL SECTION, COMPOSITE, SMEAR ALL LAYERS

Property module: Homogeneous shell section editor: Section integration: Before analysis; Basic: Idealization: Membrane only or Bending only

Property module: Composite shell section editor: Section integration:
Before analysis; Basic: Idealization: Membrane only, Bending only,
or Smear all layers

Property module: Shell (conventional or continuum) composite layup editor: 
Section integration: Before analysis; Basic: Idealization: Membrane only, Bending only, or Smear all layers

You can define the distance (measured as a fraction of the shell's thickness) from the shell's midsurface to the reference surface containing the element's nodes (see Defining the initial geometry of conventional shell elements). Positive values of the offset are in the positive normal direction (see About shell elements). When the offset is set equal to 0.5, the top surface of the shell is the reference surface. When the offset is set equal to −0.5, the bottom surface is the reference surface. The default offset is 0, which indicates that the middle surface of the shell is the reference surface.

You can specify an offset value that is greater in magnitude than 0.5. However, this technique should be used with caution in regions of high curvature. The element's area and all kinematic quantities are calculated relative to the reference surface, which may lead to a surface area integration error, affecting the stiffness and mass of the shell.

In an Abaqus/Standard analysis a spatially varying offset can be defined for conventional shells using a distribution (Distribution definition). The distribution used to define the shell offset must have a default value. The default offset is used by any shell element assigned to the shell section that is not specifically assigned a value in the distribution.

An offset to the shell's top surface is illustrated in Figure 1.

Figure 1. Schematic of shell offset for an offset value of 0.5.

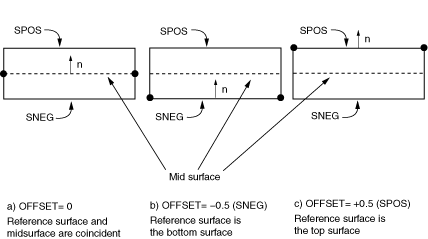
A shell offset value can be specified only if a material definition is referenced or a composite shell section is defined.

SHELL GENERAL SECTION, OFFSET=offset

Property module: composite layup editor: Section integration: Before analysis; Offset: choose a reference surface, specify an offset, or select a scalar discrete field

Property module: AssignSection: select regions: Section: select a homogeneous or composite shell section: Definition: select a reference surface, specify an offset, or select a scalar discrete field

You can define a spatially varying thickness for conventional shells using a distribution (Distribution definition). The thickness of continuum shell elements is defined by the element geometry.

For composite shells the total thickness is defined by the distribution, and the layer thicknesses you specify are scaled proportionally such that the sum of the layer thicknesses is equal to the total thickness (including spatially varying layer thicknesses defined with a distribution).

The distribution used to define shell thickness must have a default value. The default thickness is used by any shell element assigned to the shell section that is not specifically assigned a value in the distribution.

If the shell thickness is defined for a shell section with a distribution, nodal thicknesses cannot be used for that section definition.

SHELL SECTION, SHELL THICKNESS=distribution name

Property module: composite layup editor: Section integration: Before analysis; Shell Parameters: Shell thickness: Element distribution: select an analytical field or an element-based discrete field

Property module: shell section editor: Section integration: Before analysis; Basic: Shell thickness: Element distribution: select an analytical field or an element-based discrete field

Property module: shell section editor: Section integration: Before analysis; Advanced: Shell thickness: Element distribution: select an analytical field or an element-based discrete field

You can define a conventional shell with continuously varying thickness by specifying the thickness of the shell at the nodes. This method can be used only if the section is defined in terms of material properties; it cannot be used if the section behavior is defined by specifying the equivalent section properties directly. For continuum shell elements a continuously varying thickness can be defined through the element nodal geometry; hence, the nodal thickness is not meaningful.

If you indicate that the nodal thicknesses will be specified, for homogeneous shells any constant shell thickness you specify will be ignored, and the shell thickness will be interpolated from the nodes. The thickness must be defined at all nodes connected to the element.

For composite shells the total thickness is interpolated from the nodes, and the layer thicknesses you specify are scaled proportionally such that the sum of the layer thicknesses is equal to the total thickness (including spatially varying layer thicknesses defined with a distribution).

If the shell thickness is defined for a shell section with a distribution, nodal thicknesses cannot be used for that section definition. However, if nodal thicknesses are used, you can still use distributions to define spatially varying thicknesses on the layers of conventional shell elements.

NODAL THICKNESS
SHELL GENERAL SECTION, NODAL THICKNESS

Property module: composite layup editor: Section integration: Before analysis; Shell Parameters: Nodal distribution: select an analytical field or a node-based discrete field

Property module: shell section editor: Section integration: Before analysis; Basic: Nodal distribution: select an analytical field or a node-based discrete field

Property module: shell section editor: Section integration: Before analysis; Advanced: Nodal distribution: select an analytical field or a node-based discrete field

Abaqus allows for a possible uniform change in the shell thickness in a geometrically nonlinear analysis (see Change of shell thickness). The Poisson’s strain is based on a fixed section Poisson’s ratio, either user specified or computed by Abaqus based on the elastic portion of the material definition.

By default, Abaqus computes the Poisson’s strain using a fixed section Poisson’s ratio of 0.5.

SHELL GENERAL SECTION, POISSON=${\nu }_{eff}$

SHELL GENERAL SECTION, POISSON=ELASTIC

Property module: composite layup editor: Section integration: Before analysis; Shell Parameters: Section Poisson's ratio: Use analysis default or Specify value: ${\nu }_{eff}$

Property module: shell section editor: Section integration: Before analysis; Advanced: Section Poisson's ratio: Use analysis default or Specify value: ${\nu }_{eff}$

The thickness modulus is used in computing the stress in the thickness direction (see Thickness direction stress in continuum shell elements). Abaqus computes a thickness modulus value by default based on the elastic portion of the material definitions in the initial configuration. Alternatively, you can provide a value.

If the material properties are unavailable during the preprocessing stage of input; for example, when the material behavior is defined by the fabric material model or user subroutine UMAT or VUMAT, you must specify the effective thickness modulus directly.

SHELL GENERAL SECTION, THICKNESS MODULUS=$E_{eff}$

Property module: composite layup editor: Section integration: Before analysis; Shell Parameters: Thickness modulus $E_{eff}$ to specify the thickness properties directly

Property module: shell section editor: Section integration: Before analysis; Advanced:  Thickness modulus $E_{eff}$ to specify the thickness properties directly

You can provide nondefault values of the transverse shear stiffness. You must specify the transverse shear stiffness for shear flexible shells in Abaqus/Standard if the section properties are specified in user subroutine UGENS. If you do not specify the transverse shear stiffness, it will be calculated as described in Shell section behavior.

SHELL GENERAL SECTION
TRANSVERSE SHEAR STIFFNESS

Property module: composite layup editor: Section integration: Before analysis; Shell Parameters: toggle on Specify transverse shear

Property module: shell section editor: Section integration: Before analysis; Advanced: toggle on Specify transverse shear

You can define initial stresses (see Defining initial stresses) for general shell sections that will be applied as initial section forces and moments. Initial conditions can be specified only for the membrane forces, the bending moments, and the twisting moment. Initial conditions cannot be prescribed for the transverse shear forces.

In Abaqus/Explicit you can specify second-order accuracy in the shell element formulation. See Section controls for more information.

SHELL GENERAL SECTION, CONTROLS=name

Mesh module: MeshElement Type: Element Controls

You can specify a nondefault hourglass control formulation or scale factors for elements that use reduced integration. See Section controls for more information.

In Abaqus/Standard the nondefault enhanced hourglass control formulation is available only for S4R and SC8R elements.

In Abaqus/Standard you can modify the default values for hourglass control stiffness based on the default total stiffness approach for elements that use hourglass control and define a scaling factor for the stiffness associated with the drill degree of freedom (rotation about the surface normal) for elements that use six degrees of freedom at a node.

No default values are available for hourglass control stiffness if the section properties are specified in user subroutine UGENS. Therefore, you must specify the hourglass control stiffness when UGENS is used to specify the section properties for reduced-integration elements.

The stiffness associated with the drill degree of freedom is the average of the direct components of the transverse shear stiffness multiplied by a scaling factor. In most cases the default scaling factor is appropriate for constraining the drill rotation to follow the in-plane rotation of the element. If an additional scaling factor is defined, the additional scaling factor should not increase or decrease the drill stiffness by more than a factor of 100.0 for most typical applications. Usually, a scaling factor between 0.1 and 10.0 is appropriate.

There are no hourglass stiffness factors or scale factors for hourglass stiffness for the nondefault enhanced hourglass control formulation. You can define the scale factor for the drill stiffness for the nondefault enhanced hourglass control formulation.

SECTION CONTROLS, NAME=name
SHELL GENERAL SECTION, CONTROLS=name

SHELL GENERAL SECTION
HOURGLASS STIFFNESS

Mesh module: MeshElement Type: Element Controls

You can define the mass per unit area for conventional shell elements whose section properties are specified directly in terms of the section stiffness (either directly in the section definition or, in Abaqus/Standard, in user subroutine UGENS). The density is required, for example, in a dynamic analysis or for gravity loading. See Density for details.

The density is defined as part of the material definition for shells whose section properties include a material definition.

This functionality is similar to the more general functionality of defining a nonstructural mass contribution (see Nonstructural mass definition.) The only difference between the two definitions is that the nonstructural mass contributes to the rotary inertia terms about the midsurface while the additional mass defined in the section definition does not.

SHELL GENERAL SECTION, ELSET=name, DENSITY=$\rho$

SHELL GENERAL SECTION, ELSET=name, USER, 
DENSITY=$\rho$ 

Property module: composite layup editor: Section integration: Before analysis; Shell Parameters: toggle on Density, and enter $\rho$

Property module: shell section editor: Section integration: Before analysis; Advanced: toggle on Density, and enter $\rho$ 

You can include mass and stiffness proportional damping in a shell section definition. See Material damping for more information about material damping in Abaqus.

Temperatures and field variables can be specified by defining the value at the reference surface of the shell or by defining the values at the nodes of a continuum shell element. The actual values of the temperatures and field variables are specified as either predefined fields or initial conditions (see Predefined Fields or Initial conditions in Abaqus/Standard and Abaqus/Explicit).

The following output variables are available from Abaqus/Explicit as element output: section forces and moments, section strains, element energies, element stable time increment, and element mass scaling factor.

The output that is available from Abaqus/Standard depends on how the section behavior is defined.

Output if the section is defined in terms of material properties

For shells whose section properties include a material definition (homogeneous or composite), section forces and moments and section strains are available as element output. The section moments are calculated relative to the reference surface. In addition, stress (in-plane and, for certain elements, transverse shear), strain, and orthotropic failure measures can be output. Since the behavior of the material is linear, three section points per layer (the bottom, middle, and top, respectively) are available for output. Stress invariants and principal stresses are not available as output but can be visualized in Abaqus/CAE.

Output if the equivalent section properties are specified directly or in UGENS

If the $\left[\mathbf{D}\right]$ matrix is used to specify the equivalent section properties directly or if user subroutine UGENS is used, section point stresses and strains and section strains are not available for output or visualization inAbaqus/CAE; only section forces and moments can be requested for outputor visualized inAbaqus/CAE.