Random response analysis

Random response analysis predicts the response of a system that is subjected to a nondeterministic continuous excitation that is expressed in a statistical sense by a cross-spectral density matrix. Since the loading is nondeterministic, it can be characterized only in a statistical sense; Abaqus/Standard assumes that the excitation is stationary and ergodic. These statistical measures are explained in detail in Random response analysis. The random response procedure can, for example, be used to determine the response of an airplane to turbulence, the response of a car to road surface imperfections, the response of a structure to jet noise, or the response of a building to an earthquake.

In the most general case the excitation is defined as a frequency-dependent cross-spectral density (CSD) matrix. Except in cases involving moving noise or user subroutine UCORR, it is assumed that for a given load case the CSD matrix can be separated into a product of a frequency-dependent, complex-valued scalar function and a frequency-independent, complex-valued, spatial correlation matrix. This assumption helps reduce both the computational time and the amount of required user input but implies that each element of the CSD matrix in a given load case has the same frequency dependence. You can define a different frequency dependence for each load case, but the loads in one load case will not be correlated with loads in another. Consequently, the system CSD matrix is assembled by simply summing (superimposing) the CSD matrices of the individual load cases.

The frequency-dependent scalar function can be composed of a weighted sum of user-defined, complex-valued, frequency functions. These user-defined frequency functions are specified in units of power spectral density. You assign weights to each frequency function as well as specify properties of the spatial correlation matrix that defines the correlation between excitations at different locations and in different directions for a particular load case. Frequency functions and correlations are discussed below; see Defining the frequency functions and Defining the correlation.

The loads can be defined as concentrated point loads, as distributed loads, as connector element loads, or as base motion excitations, as described below in Boundary conditions and Loads. Multiple, uncorrelated load cases can be defined for concentrated point loads, connector loads, and base motions. Load case 1 is reserved for all distributed loads defined in a particular step. In these steps load case 1 cannot be used for any concentrated point load, connector load, or base motion. Thus, there cannot be any correlation between distributed loads and any other load. Moreover, base motion excitations are assumed to be statistically independent (no correlation) with any other load type even when the same load case number is used. The concentrated point and connector element loads are assumed to be correlated if the same load case number is used.

The random response procedure is based on using a subset of the modes of the system, which must first be extracted by using the eigenfrequency extraction procedure. The modes will include eigenmodes and, if activated in the eigenfrequency extraction step, residual modes. The number of modes extracted must be sufficient to model the dynamic response of the system adequately, which is a matter of judgment on your part. The model can be preloaded prior to the eigenfrequency extraction. Initial stress effects are included in the stiffness used in the eigenfrequency extraction if geometric nonlinearities are included in the general analysis procedure used to apply the preloads (General and perturbation procedures).

The random response of the model is expressed as power spectral density values of nodal and element variables, as well as their root mean square values.

Defining the frequency range

You specify the frequency range of interest for the random response procedure. The response is calculated at multiple points between the lowest frequency of interest and the first eigenfrequency in the range, between each eigenfrequency in the range, and between the last eigenfrequency in the range and the highest frequency in the range as illustrated in Figure 1. The default number of calculation points in each interval is 20; you can change this number when you define the step. Accurate RMS values can be obtained only if enough points are used so that Abaqus/Standard can integrate accurately over the frequency range. The bias function allows the points on the frequency scale to be spaced closer together at the eigenfrequencies, thus allowing detailed definition of the response close to resonant frequencies and more accurate integration.

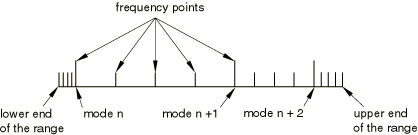
Figure 1. Division of range using modes and 5 calculation points.

Input File Usage

RANDOM RESPONSE
lower_freq_limit, upper_freq_limit, num_calc_pts, bias_parameter, freq_scale

Abaqus/CAE Usage

Step module: Create Step: Linear perturbation: Random response

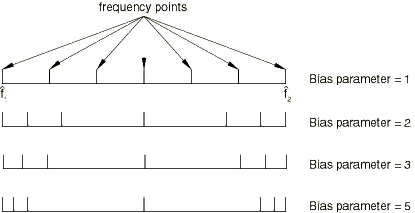
The bias parameter

The bias parameter can be used to provide closer spacing of the result points either toward the middle or toward the ends of each frequency interval. Figure 2 shows a few examples of the effect of the bias parameter on the frequency spacing.

Figure 2. Effect of the bias parameter on the frequency spacing for a number of points

n = 7

The bias formula used to calculate the frequency at which results are presented is as follows:

{\hat{f}}_{k} = \frac{1}{2} ({\hat{f}}_{1} + {\hat{f}}_{2}) + \frac{1}{2} ({\hat{f}}_{2} - {\hat{f}}_{1}) {| y |}^{1 / p} sign (y),

where

y: $= - 1 + 2 (k - 1) / (n - 1)$ ;
n: is the number of frequency points at which results are to be given;
k: is one such frequency point ( $k = 1, 2, \dots, n$ );
${\hat{f}}_{1}$: is the lower limit of the frequency interval;
${\hat{f}}_{2}$: is the upper limit of the interval;
${\hat{f}}_{k}$: is the frequency at which the kth results are given;
p: is the bias parameter value; and
$\hat{f}$: is the frequency or the logarithm of the frequency, depending on the chosen frequency scale.

A bias parameter, p, that is greater than 1.0 provides closer spacing of the results points toward the ends of each frequency interval (as shown in the examples above), while values of p that are less than 1.0 provide closer spacing toward the middle of each frequency interval. The default value of the bias parameter for random response analysis is 3.0.

Defining the frequency functions

To define the random loading, you specify a frequency function and a cross-correlation definition that refers to the frequency function. The frequency functions are defined as model data (i.e., they are step independent) and must be named. A log-log scale is used in interpolating between the given values.

The type of units in the CSD matrix of the excitation are specified as part of the frequency function definition. The default type is power units. If the CSD matrix of the excitation is due to base motion, the units must be in g units and you should define the acceleration of gravity. Alternatively, decibel units can be specified; this type of units is explained below.

Input File Usage

Use one of the following options to define the frequency function:

PSD-DEFINITION, NAME=name, TYPE=FORCE (default; power units)
PSD-DEFINITION, NAME=name, TYPE=BASE, G=g
PSD-DEFINITION, NAME=name, TYPE=DB, DB REFERENCE= $P_{ref}$

Abaqus/CAE Usage

Load module: Create Amplitude; Type: PSD Definition; Specification units:  Power, Decibel, or Gravity

Defining the cross-spectral density matrix in decibel units

In Abaqus/Standard the decibel value $d b (f)$ is related to the frequency function $P (f)$ by the following full octave band conversion formula:

d b (f) = 10 \log_{10} \frac{P (f)}{\sqrt{2} P_{ref} / f_{c}},

where $P_{ref}$ is the user-specified reference power and $f_{c}$ is the midband frequency (see Table 1).

Table 1. Standard octave bands.
Band number	Band center (frequency, Hz)
1	1.0
2	2.0
3	4.0
4	8.0
5	16.0
6	31.5
7	63.0
8	125.0
9	250.0
10	500.0
11	1000.0
12	2000.0
13	4000.0
14	8000.0
15	16000.0

Hence, the frequency function follows from the function defined in decibel units as

P (f) = \frac{\sqrt{2}}{f_{c}} P_{ref} 10^{d b (f) / 10} .

If you have data in terms of an alternative frequency scale (e.g., one-third octave band), an equivalent full octave band power reference value can be obtained as described in Random response analysis.

$P (f)$ in decibels must be specified as a function of the frequency band; the associated midband frequencies are given in Table 1.

Alternate methods for defining frequency functions

You can define a frequency function in an external file or in a user subroutine.

Defining the frequency function in an external file

The data to define a frequency function can be contained in an external file.

Input File Usage

PSD-DEFINITION, NAME=name, TYPE=type, INPUT=file name

Abaqus/CAE Usage

Load module: Create Amplitude; Type: PSD Definition; Specification units:  Power, Decibel, or Gravity; Real, Imaginary, Frequency

Defining the frequency function in a user subroutine

Complicated frequency functions can be more easily defined by user subroutine UPSD than by entering data directly.

Input File Usage

PSD-DEFINITION, NAME=name, TYPE=type, USER

Any data lines given will be ignored if the USER parameter is specified.

Abaqus/CAE Usage

Load module: Create Amplitude; Type: PSD Definition; Specification units:  Power or Gravity; toggle on Specify data in an external user subroutine

Defining the correlation

You define the cross-correlation between the applied nodal loads or base motions. You can also assign scaling (weight) factors to the frequency functions through the cross-correlation definition. Distributed loads are converted to equivalent nodal loads, which are treated as individual point loads with respect to the cross-correlation. The cross-correlation is defined in the random response step and references a particular load case number and frequency function.

Three types of correlation can be defined: correlated, uncorrelated, and moving noise. As many correlations as needed to define the random loading can be specified unless the moving noise type is chosen, in which case only one correlation can appear in the step definition.

For the correlated type all terms in the cross-spectral density matrix are considered, which implies that the loads on all degrees of freedom within the load case are fully correlated (statistically dependent on each other).
For the uncorrelated type only diagonal terms in the cross-spectral density matrix are considered, which implies that no correlation exists between the load on one degree of freedom and the load on another. You should exercise caution when choosing the uncorrelated type with distributed loads since the equivalent nodal forces would be uncorrelated with each other (statistically independent).
For the moving noise type the terms in the correlation matrix depend on the relative position of the points where the loads are applied. This type can be used only in conjunction with concentrated point loads and distributed loads. In addition, the moving noise formulation assumes that the frequency function referenced by the cross-correlation defines a reference power spectral density function of the noise source. (It is a reference power spectral density because it can later be scaled by the magnitude of the loadings specified as distributed, concentrated point, or connector element loads.) Since the power spectral density is real-valued for real-valued variables, the frequency function must not contain imaginary terms when used with the moving noise type of cross-correlation.

Input File Usage

Use one of the following options to define the correlation:

CORRELATION, TYPE=CORRELATED, PSD=name
CORRELATION, TYPE=UNCORRELATED, PSD=name
CORRELATION, TYPE=MOVING NOISE

For the moving noise type the reference to the power spectral density function must be given on each data line.

Abaqus/CAE Usage

Load module; Create Boundary Condition; Step: random_response_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion; Correlation tabbed page: toggle on Specify correlation; Approach: Correlated or Uncorrelated; PSD:  psd_amplitude_name

Specifying whether the correlation matrix is complex

For correlated or uncorrelated cross-correlations you can specify whether or not both real and imaginary terms will be included in the spatial correlation matrix. This specification does not affect the imaginary terms given for the power spectral density frequency function.

Input File Usage

Use one of the following options:

CORRELATION, TYPE=CORRELATED, COMPLEX=YES or NO, 
PSD=name
CORRELATION, TYPE=UNCORRELATED, COMPLEX=YES or NO, 
PSD=name

Abaqus/CAE Usage

Load module; Create Boundary Condition; Step: random_response_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion; Correlation tabbed page: toggle on Specify correlation; Approach: Correlated or Uncorrelated; PSD:  psd_amplitude_name; Real; Imaginary

Alternate methods for defining a correlation

You can define a correlation in an external input file or in a user subroutine.

Defining the correlation in an external input file

The data to define a correlation can be contained in an external input file.

Input File Usage

CORRELATION, TYPE=type, PSD=name, INPUT=file_name

Abaqus/CAE Usage

You cannot define a correlation in an external file in Abaqus/CAE.

Defining the correlation in a user subroutine

Simple excitations, such as uncorrelated white noise, are easily defined. Excitations involving more complicated correlations, including cases where the elements of the CSD matrix have different frequency dependencies, can be defined through user subroutine UCORR. If the user subroutine is specified, only the load case number must be entered as part of the correlation definition. A user subroutine cannot be used to define a moving noise correlation.

For uncorrelated cross-correlations only the diagonal terms of the correlation matrix specified in UCORR will be used. The combination of the cross-correlation with the various kinds of applied loads is discussed in more detail below.

Input File Usage

Use one of the following options:

CORRELATION, TYPE=CORRELATED, USER, COMPLEX=YES or NO, PSD=name
CORRELATION, TYPE=UNCORRELATED, USER, PSD=name

Abaqus/CAE Usage

Load module; Create Boundary Condition; Step: random_response_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion; Correlation tabbed page: toggle on Specify correlation; Approach: User

Selecting the modes and specifying damping

You can select the modes to be used in modal superposition and specify damping values for all selected modes.

Selecting the modes

You can select modes by specifying the mode numbers individually, by requesting that Abaqus/Standard generate the mode numbers automatically, or by requesting the modes that belong to specified frequency ranges. If you do not select the modes, all modes extracted in the prior eigenfrequency extraction step, including residual modes if they were activated, are used in the modal superposition.

Input File Usage

Use one of the following options to select the modes by specifying mode numbers:

SELECT EIGENMODES, DEFINITION=MODE NUMBERS
SELECT EIGENMODES, GENERATE, DEFINITION=MODE NUMBERS

Use the following option to select the modes by specifying a frequency range:

SELECT EIGENMODES, DEFINITION=FREQUENCY RANGE

Abaqus/CAE Usage

You cannot select the modes in Abaqus/CAE; all modes extracted are used in the modal superposition.

Specifying damping

Damping is almost always specified for a random response analysis (see Material damping). If damping is absent, the response of a structure will be unbounded if the forcing frequency is equal to an eigenfrequency of the structure. To get quantitatively accurate results, especially near natural frequencies, accurate specification of damping properties is essential. The various damping options available are discussed in Material damping. You can define a damping coefficient for all or some of the modes used in the response calculation. The damping coefficient can be given for a specified mode number or for a specified frequency range. When damping is defined by specifying a frequency range, the damping coefficient for a mode is interpolated linearly between the specified frequencies. The frequency range can be discontinuous; the average damping value will be applied for an eigenfrequency at a discontinuity. The damping coefficients are assumed to be constant outside the range of specified frequencies.

Input File Usage

Use the following option to define damping by specifying mode numbers:

MODAL DAMPING, DEFINITION=MODE NUMBERS

Use the following option to define damping by specifying a frequency range:

MODAL DAMPING, DEFINITION=FREQUENCY RANGE

Abaqus/CAE Usage

Use the following input to define damping by specifying mode numbers:

Step module: Create Step: Linear perturbation: Random response: 
Damping

Defining damping by specifying frequency ranges is not supported in Abaqus/CAE.

Example of specifying damping

Figure 3 illustrates how the damping coefficients at different eigenfrequencies are determined for the following input:

MODAL DAMPING, DEFINITION=FREQUENCY RANGE
 $f_{1}, d_{1}$ 
 $f_{2}, d_{2}$ 
 $f_{2}, d_{3}$ 
 $f_{3}, d_{3}$ 
 $f_{4}, d_{4}$

Figure 3. Damping values specified by frequency range.

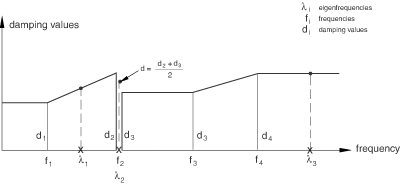
Rules for selecting modes and specifying damping coefficients

The following rules apply for selecting modes and specifying modal damping coefficients:

No modal damping is included by default.
Mode selection and modal damping must be specified in the same way, using either mode numbers or a frequency range.
If you do not select any modes, all modes extracted in the prior frequency analysis, including residual modes if they were activated, will be used in the superposition.
If you do not specify damping coefficients for modes that you have selected, zero damping values will be used for these modes.
Damping is applied only to the modes that are selected.
Damping coefficients for selected modes that are beyond the specified frequency range are constant and equal to the damping coefficient specified for the first or the last frequency (depending which one is closer). This is consistent with the way Abaqus interprets amplitude definitions.

Initial conditions

It is not appropriate to specify initial conditions in a random response analysis.

Boundary conditions

It is not possible to prescribe nonzero displacements and rotations directly as boundary conditions (Boundary conditions in Abaqus/Standard and Abaqus/Explicit) in mode-based dynamic response procedures. Therefore, in a random response analysis the motion of nodes can be specified only as base motion; nonzero displacement, velocity, or acceleration history definitions given as boundary conditions are ignored, and any changes in the support conditions from the eigenfrequency extraction step are flagged as errors. In addition, any amplitude definitions are ignored in a random response analysis.

The method for prescribing motion in modal superposition procedures is described in Transient modal dynamic analysis. In random response analysis only a single (primary) base can be defined.

Defining multiple load cases

The excitation defined by the base motion is assigned to numbered load cases. These load cases are then referenced in the cross-correlation definition. The load cases are associated with frequency functions through the reference in the cross-correlation definition. Any number of load cases can be defined, but load case number 1 cannot be used if distributed loads are defined in the same step.

Input File Usage

BASE MOTION, LOAD CASE=n

Abaqus/CAE Usage

Base motions with load cases are not supported in Abaqus/CAE.

Converting base motion excitation to a cross-spectral density matrix

When the excitation is provided by a base motion, it is converted directly into a cross-spectral density matrix projected onto the eigenspace through the modal participation factors (see Natural frequency extraction), giving

S_{α β} (f) = {\begin{matrix} \sum_{J} g_{J}^{2} P^{J} (f) \sum_{i} \sum_{j} Γ_{α}^{i} Γ_{β}^{j} \sum_{I} Ψ_{i j}^{I J} {(2 π f)}^{2 λ_{I}} & for α < β, \\ {[S_{β α} (f)]}^{*} & for α > β, \\ Re (\sum_{J} g_{J}^{2} P^{J} (f) \sum_{i} \sum_{j} Γ_{α}^{i} Γ_{β}^{j} \sum_{I} Ψ_{i j}^{I J} {(2 π f)}^{2 λ_{I}}) & for α = β, \end{matrix}

where the superscript ^* denotes complex conjugate and where

$Γ_{α}^{i}$: is the modal participation factor for mode $α$ in excitation direction i (i=1–6);
$P^{J} (f)$: is the frequency function referenced by the Jth cross-correlation and defined as a function of the frequency f in g units;
$Ψ_{i j}^{I J}$: is a matrix of weight factors indicating the fraction of $P^{J}$ to be associated with the correlation between base motion in directions i and j for load case I, as described below;
$λ_{I}$: $= 0$ , 1, or 2, depending on whether the base motion corresponding to load case I is defined in terms of an acceleration spectrum, a velocity spectrum, or a displacement spectrum (see Transient modal dynamic analysis); and
$g_{J}$: is the user-specified acceleration of gravity for the same power spectral density frequency function that defines $P^{J}$ .

If the cross-correlation is defined in user subroutine UCORR, $Ψ_{i j}^{I J}$ is defined in the user subroutine. Otherwise,

$Ψ_{i j}^{I J}$: $= a^{I J}$ for all $(i, j)$ if the excitation is correlated or
: $= a^{I J} δ_{i j}$ if the excitation is uncorrelated,

where $a^{I J}$ is the (complex) value of the weight factor by which to scale the frequency function $P^{J}$ used in load case I.

Loads

The loading for random response analysis is defined in general terms by the cross-spectral density matrix $S_{(N, i) (M, j)} (f)$ , where f is frequency in cycles per time and the subscripts $(N, i)$ and $(M, j)$ refer to degree of freedom i at node N and degree of freedom j at node M, respectively. Distributed loads are converted to equivalent nodal loads, which—for the formulation of the correlation matrix—are treated in the same way as concentrated point loads. The units of $S_{(N, i) (M, j)} (f)$ are (force)² or (moment)² per frequency. In addition, any amplitude references on the concentrated point, connector element, or distributed load definitions are ignored in a random response analysis.

Defining multiple load cases

Distributed loads will be assigned automatically to load case number 1. You assign a concentrated point load or connector element load to a numbered load case. Any number of concentrated point and connector element load cases can be specified, but load case number 1 cannot be used for a concentrated point or connector element load if a distributed load is present in the same step. The concentrated point, connector element, and distributed load cases are associated with frequency functions through the cross-correlation definition.

Input File Usage

Use one or more of the following options:

CLOAD, LOAD CASE=n
CONNECTOR LOAD, LOAD CASE=m
DLOAD

Correlated and uncorrelated loading

For correlated or uncorrelated cross-correlations, the cross-spectral density matrix is defined as

S_{(N, i) (M, j)} (f) = {\begin{matrix} \sum_{J} P^{J} (f) \sum_{I} C_{(N, i) (M, j)}^{I J} F_{(N, i)}^{I} F_{(M, j)}^{I} & for (N, i) < (M, j), \\ {[S_{(M, i) (N, j)} (f)]}^{*} & for (N, i) > (M, j), \\ Re (\sum_{J} P^{J} (f) \sum_{I} C_{(N, i) (M, j)}^{I J} F_{(N, i)}^{I} F_{(M, j)}^{I}) & for (N, i) = (M, j), \end{matrix}

where the superscript ^* denotes complex conjugate and where

$F_{(N, i)}^{I}$: is the load magnitude applied to degree of freedom i at node N for load case I;
$P^{J} (f)$: is the frequency function referenced by the Jth cross-correlation and defined as a function of the frequency f in power (force) or decibel units; and
$C_{(N, i) (M, j)}^{I J}$: is a matrix of weight factors indicating the fraction of $P^{J}$ to be associated with the $(N, i) (M, j)$ cross-correlation term for load case I, as described below.

If the cross-correlation is defined in user subroutine UCORR, $C_{(N, i) (M, j)}^{I J}$ is defined in the user subroutine. Otherwise,

$C_{(N, i) (M, j)}^{I J}$: $= a^{I J}$ for all $(N, M, i, j)$ if the excitation is correlated or
: $= a^{I J} δ_{N M} δ_{i j}$ if the excitation is uncorrelated,

where $a^{I J}$ is the (complex) value of the weight factor by which to scale the frequency function $P^{J}$ used in load case I.

Moving noise loading

For moving noise cross-correlations, the cross-spectral density matrix is defined as

S_{(N, i) (M, j)} (f) = \sum_{I} P^{I} (f) \exp (i 2 π f (x_{N} - x_{M}) \cdot v^{I} \frac{1}{v^{I} \cdot v^{I}}) F_{(N, i)}^{I} F_{(M, j)}^{I},

where

$F_{(N, i)}^{I}$: is the load magnitude applied to degree of freedom i at node N for load case I;
$P^{I} (f)$: is the reference power spectral density function associated with load case I and defined as a function of the frequency f in power (force) or decibel units;
$v^{I}$: is the velocity vector of noise propagation given for load case I; and
$x_{N}$: are the coordinates of node N.

This definition of moving noise implies that the different noise sources have no cross-correlation. Therefore, it is most generally used with only one noise source ( $I = 1$ only). In addition, since $P^{I} (f)$ is the actual power spectral density of the moving noise source, it must be defined as a real-valued function.

Predefined fields

Predefined fields, including temperature, cannot be used in random response analysis.

Material options

As in any dynamic analysis procedure, mass or density (Density) must be assigned to some regions of any separate parts of the model where dynamic response is required. The following material properties are not active during a random response analysis: plasticity and other inelastic effects, rate-dependent properties, thermal properties, mass diffusion properties, electrical properties, and pore fluid flow properties (see General and perturbation procedures).

Elements

Other than generalized axisymmetric elements with twist, any of the stress/displacement elements in Abaqus/Standard can be used in a random response analysis (see Choosing the appropriate element for an analysis type).

Output

In random response analysis the value of a variable is its power spectral density; all of the output variables in Abaqus/Standard are listed in Abaqus/Standard output variable identifiers. Power spectral density values are not available for concentrated and distributed loads and for SINV.

Options are also provided in random response analysis to obtain root mean square values for certain variables, as listed below. Total values include base motion, while relative values are measured relative to the base motion.

Element integration point variables:

RS: Root mean square of all stress components.
RE: Root mean square of all strain components.

Element nodal point variables:

MISES: Mises equivalent stress..
RMISES: Root mean square of Mises equivalent stress.

For connector elements, the following element output variables are available:

RCTF: Root mean square of connector total forces.
RCEF: Root mean square of connector elastic forces.
RCVF: Root mean square of connector viscous forces.
RCRF: Root mean square of connector reaction forces.
RCSF: Root mean square of connector friction forces.
RCU: Root mean square of connector relative displacements.
RCCU: Root mean square of connector constitutive displacements.

Nodal variables:

RU: Root mean square values of all components of the relative displacement/rotation at a node.
RTU: Root mean square values of all components of the total displacement/rotation at a node.
RV: Root mean square values of all components of the relative velocity at a node.
RTV: Root mean square values of all components of the total velocity at a node.
RA: Root mean square values of all components of the relative acceleration at a node.
RTA: Root mean square values of all components of the total acceleration at a node.
RRF: Root mean square values of all components of reaction forces and reaction moments at a node.

No energy values are available for a random response analysis.

To reduce the computational cost of random response analysis, you should request output only for selected element and node sets. Abaqus/Standard will calculate the response for only the element and nodal variables requested.

When MISES or RMISES output is requested, Abaqus/Standard stores the needed data in the output database (.odb) file and Abaqus/Viewer does the actual computation of the responses. These computations require element stress output in the frequency step preceding the random response step. Note that specifying the name of the element set in the output request in the random response step has no effect on these two output variables. If MISES or RMISES output for a selected set of elements is desired, the name of that element set needs to be specified for the element stress output request in the preceding frequency step. Unlike in other procedures, MISES and RMISES output for random response analysis is computed at the element nodal points and not at the element integration points.

Input file template

HEADING
…
PSD-DEFINITION, NAME=name, TYPE=type
Data lines to define a frequency function (or PSD function for moving noise)
**
STEP
FREQUENCY
Data line to control eigenvalue extraction
BOUNDARY
Data lines to assign degrees of freedom to the primary base
END STEP
STEP
RANDOM RESPONSE
Data line to specify frequency range of interest
SELECT EIGENMODES
Data lines to define the applicable mode ranges
MODAL DAMPING
Data line to define modal damping
CORRELATION, PSD=name, TYPE=type
Data lines to specify correlation for various excitation load cases (n, p)
DLOAD
Data lines to define distributed loads
CLOAD, LOAD CASE=n
Data lines to define concentrated loads in load case n
CONNECTOR LOAD, LOAD CASE=m
Data lines to define connector loads in load case m
BASE MOTION, DOF=dof, LOAD CASE=p
Data lines to define base motion p
END STEP