Transient modal dynamic analysis | ||||||||||
|
| |||||||||
ProductsAbaqus/StandardAbaqus/CAE
Modal dynamic analysis
Transient modal dynamic analysis gives the response of the model as a function of time based on a given time-dependent loading. The structure's response is based on a subset of the modes of the system, which must first be extracted using an eigenfrequency extraction procedure (Natural frequency extraction). The modes will include eigenmodes and, if activated in the eigenfrequency extraction step, residual modes. The number of modes extracted must be sufficient to model the dynamic response of the system adequately, which is a matter of judgment on your part.
The modal amplitudes are integrated through time, and the response is synthesized from these modal responses. For linear systems the modal dynamic procedure is much less expensive computationally than the direct integration of the entire system of equations performed in the dynamic procedure (Implicit dynamic analysis using direct integration).
As long as the system is linear and is represented correctly by the modes being used (which are generally only a small subset of the total modes of the finite element model), the method is also very accurate because the integration operator used is exact whenever the forcing functions vary piecewise linearly with time. You should ensure that the forcing function definition and the choice of time increment are consistent for this purpose. For example, if the forcing is a seismic record in which acceleration values are given every millisecond and it is assumed that the acceleration varies linearly between these values, the time increment used in the modal dynamic procedure should be a millisecond.
The user-specified maximum number of increments is ignored in a modal dynamic step. The number of increments is based on both the time increment and the total time chosen for the step.
While the response in this procedure is for linear vibrations, the prior response can be nonlinear and stress stiffening (initial stress) effects will be included in the response if nonlinear geometric effects were included in the step definition for the base state of the eigenfrequency extraction procedure, as explained in Natural frequency extraction.
![]()
Selecting the modes and specifying damping
You can select the modes to be used in modal superposition and specify damping values for all selected modes.
Selecting the modes
You can select modes by specifying the mode numbers individually, by requesting that Abaqus/Standard generate the mode numbers automatically, or by requesting the modes that belong to specified frequency ranges. If you do not select the modes, all modes extracted in the prior eigenfrequency extraction step, including residual modes if they were activated, are used in the modal superposition.
Input File Usage
Use one of the following options to select the modes by specifying mode numbers:
SELECT EIGENMODES, DEFINITION=MODE NUMBERS SELECT EIGENMODES, GENERATE, DEFINITION=MODE NUMBERS
Use the following option to select the modes by specifying a frequency range:
SELECT EIGENMODES, DEFINITION=FREQUENCY RANGE
Abaqus/CAE Usage
You cannot select the modes in Abaqus/CAE; all modes extracted are used in the modal superposition.
Specifying modal damping
Damping is almost always specified for a mode-based procedure; see Material damping. You can define a damping coefficient for all or some of the modes used in the response calculation. The damping coefficient can be given for a specified mode number or for a specified frequency range. When damping is defined by specifying a frequency range, the damping coefficient for a mode is interpolated linearly between the specified frequencies. The frequency range can be discontinuous; the average damping value will be applied for an eigenfrequency at a discontinuity. The damping coefficients are assumed to be constant outside the range of specified frequencies.
Input File Usage
Use the following option to define damping by specifying mode numbers:
MODAL DAMPING, DEFINITION=MODE NUMBERS
Use the following option to define damping by specifying a frequency range:
MODAL DAMPING, DEFINITION=FREQUENCY RANGE
Abaqus/CAE Usage
Use the following input to define damping by specifying mode numbers:
Step module: Create Step: Linear perturbation: Modal dynamics: Damping
Defining damping by specifying frequency ranges is not supported in Abaqus/CAE.
Example of specifying damping
Figure 1 illustrates how the damping coefficients at different eigenfrequencies are determined for the following input:
MODAL DAMPING, DEFINITION=FREQUENCY RANGE
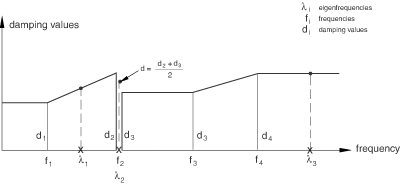
Rules for selecting modes and specifying damping coefficients
The following rules apply for selecting modes and specifying modal damping coefficients:
No modal damping is included by default.
Mode selection and modal damping must be specified in the same way, using either mode numbers or a frequency range.
If you do not select any modes, all modes extracted in the prior frequency analysis, including residual modes if they were activated, will be used in the superposition.
If you do not specify damping coefficients for modes that you have selected, zero damping values will be used for these modes.
Damping is applied only to the modes that are selected.
Damping coefficients for selected modes that are beyond the specified frequency range are constant and equal to the damping coefficient specified for the first or the last frequency (depending which one is closer). This is consistent with the way Abaqus interprets amplitude definitions.
Specifying global damping
For convenience you can specify constant global damping factors for all selected eigenmodes for mass and stiffness proportional viscous factors, as well as stiffness proportional structural damping. Structural damping is a commonly used damping model that represents damping as complex stiffness. This representation causes no difficulty for frequency domain analysis such as steady-state dynamics for which the solution is already complex. However, the solution must remain real-valued in the time domain. To allow users to apply their structural damping model in the time domain, a method has been developed to convert structural damping to an equivalent viscous damping. This technique was designed so that the viscous damping applied in the frequency domain is identical to the structural damping if the projected damping matrix is diagonal. For further details, see Modal dynamic analysis.
Input File Usage
GLOBAL DAMPING, ALPHA=factor, BETA=factor, STRUCTURAL=factor
Abaqus/CAE Usage
Defining damping by global factors is not supported in Abaqus/CAE.
Material damping
Structural and viscous material damping (see Material damping) is taken into account in a SIM-based transient modal analysis. Since the projection of damping onto the mode shapes is performed only one time during the frequency extraction step, significant performance advantages can be achieved by using the SIM-based transient modal procedure (see Using the SIM architecture for modal superposition dynamic analyses).
If the damping operators depend on frequency, they will be evaluated at the frequency specified for property evaluation during the frequency extraction procedure.
Controlling damping
You can deactivate the structural or viscous damping in a transient modal procedure if desired.
You can also control damping of the low frequency eigenmodes in transient modal analyses. This control is useful for free structures and models with secondary base motions, and it controls all sources of damping including the modal damping. To include low frequency eigenmodes, set the low frequency cutoff value to a small negative value. To exclude them, either provide a low frequency cutoff value or allow Abaqus to calculate it; it will be six orders of magnitude smaller than the eigenfrequency of the first deformable eigenmode.
Input File Usage
Use the following option to deactivate structural and viscous damping in a specific transient modal dynamic step:
DAMPING CONTROLS, STRUCTURAL=NONE, VISCOUS=NONE
Use the following option to control damping of the low frequency eigenmodes in a specific transient modal dynamic step:
DAMPING CONTROLS, LOW FREQUENCY CUTOFF
Abaqus/CAE Usage
Damping controls are not supported in Abaqus/CAE.
![]()
Initial conditions
By default, the modal dynamic step will begin with zero initial displacements. If initial velocities have been defined (Initial conditions in Abaqus/Standard and Abaqus/Explicit), they will be used; otherwise, the initial velocities will be zero.
Alternatively, you can force the modal dynamic step to carry over the initial conditions from the immediately preceding step, which must be either another modal dynamic step or a static perturbation step:
In most cases if the immediately preceding step is a modal dynamic step, both the displacements and velocities are carried over from the end of that step and used as initial conditions for the current step. For a SIM-based analysis, you should use secondary base motion instead of primary base motion (see Prescribed motions in modal superposition procedures) to carry over the initial conditions; Abaqus issues a warning message if primary base motion is used.
If the immediately preceding step is a static perturbation step, the displacements are carried over from that step. If initial velocities have been defined (Initial conditions in Abaqus/Standard and Abaqus/Explicit), they will be used; otherwise, the initial velocities will be zero.
Input File Usage
Use the following option to begin the modal dynamic step with zero initial displacements:
MODAL DYNAMIC, CONTINUE=NO
Use the following option to force the modal dynamic step to carry over the initial conditions from the immediately preceding step:
MODAL DYNAMIC, CONTINUE=YES
Abaqus/CAE Usage
Use the following option to begin the modal dynamic step with zero initial displacements:
Step module: Create Step: Linear perturbation: Modal dynamics: Basic: Zero initial conditions
Use the following option to force the modal dynamic step to carry over the initial conditions from the immediately preceding step:
Step module: Create Step: Linear perturbation: Modal dynamics: Basic: Use initial conditions
![]()
Boundary conditions
It is not possible to prescribe nonzero displacements and rotations (or acoustic pressure) directly as boundary conditions (Boundary conditions in Abaqus/Standard and Abaqus/Explicit) in mode-based dynamic response procedures. In these procedures the motion for nodes can be specified only as base motion, as described below. Nonzero displacement or acceleration history definitions given as boundary conditions are ignored in modal superposition procedures, and any changes in the support conditions from the eigenfrequency extraction step are flagged as errors.
Prescribed motions in modal superposition procedures
Boundary conditions must be applied during the eigenfrequency extraction step to the degrees of freedom that will be prescribed in the modal dynamic procedure. These degrees of freedom are grouped into one or more “bases” (see Natural frequency extraction). The unnamed base is called the “primary” base. Named “secondary” bases must be defined by specifying boundary conditions in the frequency extraction step. A different motion can be prescribed for each base.
The far-field nodes of infinite elements are always added to the primary base in modal procedures. The far-field nodes are added to the primary base even if they are not explicitly constrained via boundary conditions.
Specifying the degree of freedom and the time history of the motion
The displacements and rotations that are associated with a base are prescribed during the modal dynamic response procedure. The base motions are fully defined by at most three global translations and three global rotations. Thus, at most one base motion can be defined for each translation and rotation component. Base motions are always specified in global directions, regardless of the use of nodal transformations. You specify the global direction (1–6) for which the base motion is being defined. If a rotation is specified about an origin that is not the origin of the coordinates, you must specify the center of rotation.
The time history of a motion must be defined by an amplitude curve (Amplitude Curves).
Input File Usage
BASE MOTION, DOF=n, AMPLITUDE=name
Abaqus/CAE Usage
Load module; Create Boundary Condition; Step: modal_dynamic_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion; Basic tabbed page: Degree-of-freedom: U1, U2, U3, UR1, UR2, or UR3; Amplitude: name
Scaling the amplitude of the base motion
The amplitude curve used to define the time history of the motion can be scaled. By default, the scaling factor is 1.0.
Input File Usage
BASE MOTION, DOF=n, AMPLITUDE=name, SCALE=n
Abaqus/CAE Usage
Load module; Create Boundary Condition; Step: modal_dynamic_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion; Basic tabbed page: Degree-of-freedom: U1, U2, U3, UR1, UR2, or UR3; Amplitude: name; Amplitude scale factor: n
Specifying the type of base motion
Base motions can be defined by a displacement, a velocity, or an acceleration history. For an acoustic pressure the displacement is used to describe an acoustic pressure history. If the prescribed excitation record is given in the form of a displacement or velocity history, Abaqus/Standard differentiates it to obtain the acceleration history. Furthermore, if the displacement or velocity histories have nonzero initial values, Abaqus/Standard will make corrections to the initial accelerations as described in Modal dynamic analysis. The default is to give an acceleration history for mechanical degrees of freedom and to give a displacement for an acoustic pressure.
Input File Usage
Use one of the following options:
BASE MOTION, DOF=n, AMPLITUDE=name, TYPE=ACCELERATION BASE MOTION, DOF=n, AMPLITUDE=name, TYPE=VELOCITY BASE MOTION, DOF=n, AMPLITUDE=name, TYPE=DISPLACEMENT
Abaqus/CAE Usage
Load module; Create Boundary Condition; Step: modal_dynamic_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion
Specifying secondary base motion
The primary base motion is specified by defining a base motion without referring to a base. If the base motion is to be applied to a secondary base, it must refer to the name of the base defined in the eigenfrequency extraction step.
For named bases you can also use degree of freedom 8 as the acoustic pressure degree of freedom. Acoustic pressure variation can be used in secondary bases only with big mass scaling. In such cases an acoustic mass is used to scale the big mass value. To specify an acoustic pressure, use the displacement base motion; to specify the first and the second derivative of acoustic pressure, use the velocity and acceleration, respectively.
Input File Usage
BASE MOTION, DOF=n, AMPLITUDE=name, BASE NAME=secondary base
Abaqus/CAE Usage
Load module; Create Boundary Condition; Step: modal_dynamic_step; Category: Mechanical; Types for Selected Step: Displacement base motion or Velocity base motion or Acceleration base motion; toggle on Secondary base: boundary_condition_name
Example
To illustrate the concept of primary and secondary bases, consider a single-bay frame with supports at nodes 1 and 4. If the input prior to the eigenfrequency extraction step includes the following boundary conditions:
degrees of freedom 1 through 6 constrained at node 1
degree of freedom 1 constrained at node 4
degrees of freedom 3 through 6 constrained at node 4
and different base motions are assigned to degree of freedom 2 at nodes 1 and 4, the following step definitions could be used:
an eigenfrequency extraction step that includes a boundary condition associated with BASE2 constraining degree of freedom 2 at node 4; and
a modal dynamic step that includes two base motion definitions: the primary base motion assigned to degree of freedom 2 that does not refer to a base and the secondary base motion assigned to degree of freedom 2 that refers to BASE2.
If boundary conditions were not given prior to the eigenfrequency extraction step, you would have to define them in the eigenfrequency extraction step. Again, the secondary base would be defined by a boundary condition with a base name.
Calculating the response of the structure
The degrees of freedom associated with the primary base are set to zero in the eigenfrequency extraction step, and primary base motions are introduced by multiplying the base acceleration with the modal participation factors. Hence, Abaqus/Standard calculates the response of the structure with respect to the primary base. If the rotational degrees of freedom are references in the primary base motion definition, the rotation is defined, as default, about the origin of the coordinate system unless you provide the center of rotation.
The degrees of freedom associated with the secondary bases are not set to zero in the eigenfrequency extraction step; instead, a “big” mass is added to each of them. Any degree of freedom in a secondary base that was constrained by a regular boundary condition in a previous general step will be released, and a big mass will be added to that degree of freedom. Secondary base motions are introduced by nodal forces, obtained by multiplying the base acceleration (or acoustic pressure) with the big mass (or acoustic big mass). Although the secondary base motions are defined in absolute terms, the response calculated at the secondary bases is relative to the motion of the primary base for the translational degrees of freedom. The rotational secondary bases are defined about the nodes included in the node sets specified in the base name definition. Therefore, you cannot change the center of rotation for secondary bases.
For a more detailed description of the base motion procedure, see Base motions in modal-based procedures.
![]()
Loads
The following loads can be prescribed in modal dynamic analysis, as described in Concentrated loads:
Concentrated nodal forces can be applied to the displacement degrees of freedom (1–6).
Distributed pressure forces or body forces can be applied; the distributed load types available with particular elements are described in Abaqus Elements Guide.
![]()
Predefined fields
Predefined temperature fields are not allowed in transient modal dynamic analysis. Other predefined fields are ignored.
![]()
Material options
The density of the material must be defined (Density). The following material properties are not active during a modal dynamic analysis: plasticity and other inelastic effects, rate-dependent material properties, thermal properties, mass diffusion properties, electrical properties (except for the electrical potential, , in piezoelectric analysis), and pore fluid flow properties. See General and perturbation procedures.
![]()
Elements
Other than generalized axisymmetric elements with twist, any of the stress/displacement elements in Abaqus/Standard (including those with temperature and pressure degrees of freedom) can be used in a modal dynamic analysis.
![]()
Output
All the output variables in Abaqus/Standard are listed in Abaqus/Standard output variable identifiers. The values of nodal solution variables U, V, and A in modal dynamics in the time domain are relative to the motion of the primary base. Hence, the sum of the relative motion and the base motion of the primary base yields the total motion; this total motion is available by requesting output variables TU, TV, and TA. In the absence of primary base motions, the relative and total motions are identical.
The following modal variables can be output to the data or results files (see Output to the Data and Results Files):
- GU
Generalized displacements for all modes.
- GV
Generalized velocities for all modes.
- GA
Generalized accelerations for all modes.
- SNE
Elastic strain energy for the entire model per each mode.
- KE
Kinetic energy for the entire model per each mode.
- T
External work for the entire model per each mode.
- BM
Base motion.
Neither element energy densities (such as the elastic strain energy density, SENER) nor whole element energies (such as the total kinetic energy of an element, ELKE) are available for output in modal dynamic analysis. However, whole model variables such as ALLIE (total strain energy) are available for mode-based procedures as output to the data or results files (see Output to the Data and Results Files).
The computational expense of a modal dynamic analysis can be decreased significantly by reducing the amount of output requested.
![]()
Input file template
HEADING … AMPLITUDE, NAME=amplitude Data lines to define amplitude variations ** STEP FREQUENCY Data line to specify the number of modes to be extracted BOUNDARY Data lines to assign degrees of freedom to the primary base BOUNDARY, BASE NAME=base Data lines to assign degrees of freedom to a secondary base END STEP ** STEP MODAL DYNAMIC Data line to control time incrementation SELECT EIGENMODES Data lines to define the applicable mode ranges MODAL DAMPING Data line to define modal damping BASE MOTION, DOF=dof, AMPLITUDE=amplitude BASE MOTION, DOF=dof, AMPLITUDE=amplitude, BASE NAME=base END STEP