Frictional behavior | ||||||||||||||
|
| |||||||||||||
ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE
Including friction properties in a contact property definition
Abaqus assumes by default that the interaction between contacting bodies is frictionless. You can include a friction model in a contact property definition for both surface-based contact and element-based contact.
Input File Usage
Use both of the following options for surface-based contact:
SURFACE INTERACTION, NAME=interaction_property_name FRICTION
Use both of the following options for element-based contact in Abaqus/Standard:
INTERFACE or GAP, ELSET=name FRICTION
Abaqus/CAE Usage
Interaction module: contact property editor: Element-based contact is not supported in Abaqus/CAE.
![]()
Changing friction properties during an analysis
The methods used to change friction properties during an analysis differ between Abaqus/Standard and Abaqus/Explicit.
Changing friction properties during an Abaqus/Standard analysis
It is possible to remove, to modify, or to add a friction model that does not involve a user subroutine to a contact property definition in any particular step of an Abaqus/Standard simulation. In some models, such as shrink-fit contact interference problems, friction should not be added until after the first steps have been completed. In other models friction might be removed or lowered to represent the introduction of a lubricant between the bodies.
You must identify which contact property definition or contact element set is being changed.
Input File Usage
Use both of the following options for surface-based contact:
CHANGE FRICTION, INTERACTION=name FRICTION
Use both of the following options for element-based contact:
CHANGE FRICTION, ELSET=name FRICTION
Abaqus/CAE Usage
Define a contact property with a new friction definition. Then change the contact property assigned to an interaction in a particular step.
Interaction module:
Contact property editor: Interaction editor: Contact interaction property: new_interaction_property_name
Element-based contact is not supported in Abaqus/CAE.
Specifying the time variation of the change in friction properties
You can specify an amplitude curve (see Amplitude Curves) to define the time variation of changes in friction coefficients and, if applicable, allowable elastic slip (see Stiffness method for imposing frictional constraints in Abaqus/Standard below) throughout the step. If you do not specify an amplitude curve, changes in these friction properties are either applied immediately at the beginning of the step or ramped up linearly over the step, depending on the default amplitude variation assigned to the step (see Defining an analysis), with some exceptions as described below. For many step types the default transition type is a linear ramping from old to new values, which helps avoid convergence problems that can occur upon sudden changes in friction properties.
Amplitude curves used to control variations in friction properties are subjected to the following restrictions:
-
a tabular or smooth step amplitude definition must be used,
-
only amplitudes with monotonically increasing values between 0.0 and 1.0 are accepted, and
-
the amplitude must be defined in terms of step time and using relative magnitudes.
The value of a friction coefficient or allowable elastic slip in effect at a given time is typically equal to the value of the property at the start of the step plus the current amplitude value times the anticipated change in property value over the step. Variations in friction properties must consider the following:
-
Changes in the type of frictional constraint enforcement method (penalty or Lagrange multiplier methods), changes between a “rough” friction model and a finite friction coefficient, and changes to friction properties other than the friction coefficient or allowable elastic slip always occur at the beginning of a step.
-
If a friction coefficient is dependent on slip rate, contact pressure, average surface temperature at the contact point, or field variables, the estimate of the final value of the friction coefficient for the step (which is used in calculating the anticipated change in the friction coefficient over the step) assumes that the current slip rate, contact pressure, etc. will remain in effect at the end of the step.
-
If a friction coefficient is changed during the first step of an analysis, its value at the start of the step is equal to zero for this calculation, regardless of the original friction definition in the model.
-
Changes in allowable elastic slip always occur at the beginning of a step when an exponential-decay friction model is used or when frictional properties are changed during the first general step or during a steady-state transport step that is preceded by a step type other than steady-state transport.
Input File Usage
CHANGE FRICTION, AMPLITUDE=name
Abaqus/CAE Usage
Time-dependent changes in friction properties are not supported in Abaqus/CAE.
Resetting the frictional properties to their default values
You can reset the frictional properties of the specified contact property definition or element set to their original values.
Input File Usage
Use either of the following options:
CHANGE FRICTION, RESET, INTERACTION=name CHANGE FRICTION, RESET, ELSET=name
In this case the FRICTION option is not needed.
Abaqus/CAE Usage
Interaction module:
Contact property editor: : Friction formulation: Frictionless
Interaction editor: Contact interaction property: default_interaction_property_name
Changing friction properties during an Abaqus/Explicit analysis
In Abaqus/Explicit the friction definition is specified as part of the model definition for a general contact analysis and as part of the history definition for a contact pair analysis. See Assigning contact properties for general contact in Abaqus/Explicit and Assigning contact properties for contact pairs in Abaqus/Explicit for information on changing aspects of any contact property definition during an Abaqus/Explicit analysis.
![]()
Using the basic Coulomb friction model
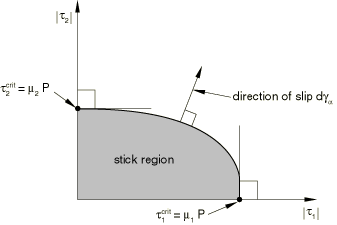
The basic concept of the Coulomb friction model is to relate the maximum allowable frictional (shear) stress across an interface to the contact pressure between the contacting bodies. In the basic form of the Coulomb friction model, two contacting surfaces can carry shear stresses up to a certain magnitude across their interface before they start sliding relative to one another; this state is known as sticking. The Coulomb friction model defines this critical shear stress, , at which sliding of the surfaces starts as a fraction of the contact pressure, p, between the surfaces (). The stick/slip calculations determine when a point transitions from sticking to slipping or from slipping to sticking. The fraction, , is known as the coefficient of friction.
For the case when the slave surface consists of a node-based surface, the contact pressure is equal to the normal contact force divided by the cross-sectional area at the contact node. In Abaqus/Standard the default cross-sectional area is 1.0; you can specify a cross-sectional area associated with every node in the node-based surface when the surface is defined or, alternatively, assign the same area to every node through the contact property definition. In Abaqus/Explicit the cross-sectional area is always 1.0, and you cannot change it.
The basic friction model assumes that is the same in all directions (isotropic friction). For a three-dimensional simulation there are two orthogonal components of shear stress, and , along the interface between the two bodies. These components act in the local tangent directions for the contact surfaces or contact elements. The local tangent directions for contact surfaces are defined in Contact formulations in Abaqus/Standard, and those for contact elements are defined in the sections describing contact modeling with those elements.
Abaqus combines the two shear stress components into an “equivalent shear stress,” , for the stick/slip calculations, where . In addition, Abaqus combines the two slip velocity components into an equivalent slip rate, . The stick/slip calculations define a surface (see Figure 1 for a two-dimensional representation) in the contact pressure–shear stress space along which a point transitions from sticking to slipping.
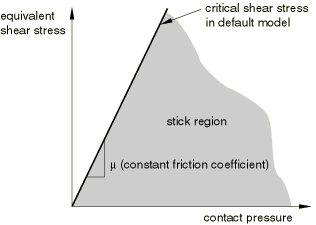
There are two ways to define the basic Coulomb friction model in Abaqus. In the default model the friction coefficient is defined as a function of the equivalent slip rate and contact pressure. Alternatively, you can specify the static and kinetic friction coefficients directly.
Using the default model
In the default model you define the coefficient of friction directly as
where is the equivalent slip rate, p is the contact pressure, is the average temperature at the contact point, and is the average predefined field variable at the contact point. , , , and are the temperature and predefined field variables at points A and B on the surfaces. Point A is a node on the slave surface, and point B corresponds to the nearest point on the opposing master surface. The temperature and field variables are interpolated along the surface at location B. If the master surface consists of a rigid body, the temperature and field variable at the reference node are used.
The friction coefficient can depend on slip rate, contact pressure, temperature, and field variables. By default, it is assumed that the friction coefficients do not depend on field variables.
The coefficient of friction can be set to any nonnegative value. A zero friction coefficient means that no shear forces will develop and the contact surfaces are free to slide. You do not need to define a friction model for such a case.
Input File Usage
FRICTION, DEPENDENCIES=n , , p, ,
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Penalty: Friction
If necessary, toggle on Use slip-rate-dependent data, Use contact-pressure-dependent data, and/or Use temperature-dependent data; and/or specify the Number of field variable dependencies in addition to slip rate, contact pressure, and temperature.
Specifying static and kinetic friction coefficients
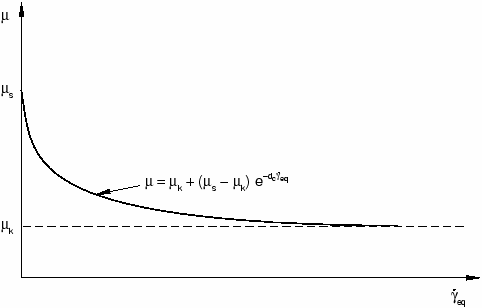
Experimental data show that the friction coefficient that opposes the initiation of slipping from a sticking condition is different from the friction coefficient that opposes established slipping. The former is typically referred to as the “static” friction coefficient, and the latter is referred to as the “kinetic” friction coefficient. Typically, the static friction coefficient is higher than the kinetic friction coefficient.
In the default model the static friction coefficient corresponds to the value given at zero slip rate, and the kinetic friction coefficient corresponds to the value given at the highest slip rate. The transition between static and kinetic friction is defined by the values given at intermediate slip rates. In this model the static and kinetic friction coefficients can be functions of contact pressure, temperature, and field variables.
Abaqus also provides a model to specify a static and a kinetic friction coefficient directly. In this model it is assumed that the friction coefficient decays exponentially from the static value to the kinetic value according to the formula:
where is the kinetic friction coefficient, is the static friction coefficient, is a user-defined decay coefficient, and is the slip rate (see Oden, J. T. and J. A. C. Martins, 1985). This model can be used only with isotropic friction and does not allow dependence on contact pressure, temperature, or field variables. There are two ways of defining this model.
Providing the static, kinetic, and decay coefficients directly
You can provide the static friction coefficient, the kinetic friction coefficient, and the decay coefficient directly (see Figure 2).
Input File Usage
FRICTION, EXPONENTIAL DECAY , ,
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Static-Kinetic Exponential Decay: Friction, Definition: Coefficients
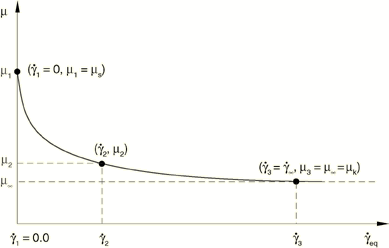
Using test data to fit the exponential model
Alternatively, you can provide test data points to fit the exponential model. At least two data points must be provided. The first point represents the static coefficient of friction specified at , and the second point, (, ) (shown in Figure 3), corresponds to an experimental measurement taken at a reference slip rate . An additional data point can be specified to characterize the exponential decay. If this additional data point is omitted, Abaqus will automatically provide a third data point, (, ), to model the assumed asymptotic value of the friction coefficient at infinite velocity. In such a case is chosen such that .
Input File Usage
FRICTION, EXPONENTIAL DECAY, TEST DATA ,
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Static-Kinetic Exponential Decay: Friction, Definition: Test data
![]()
Using the optional shear stress limit
You can specify an optional equivalent shear stress limit, , so that, regardless of the magnitude of the contact pressure stress, sliding will occur if the magnitude of the equivalent shear stress, , reaches this value (see Figure 4). A value of zero is not allowed.
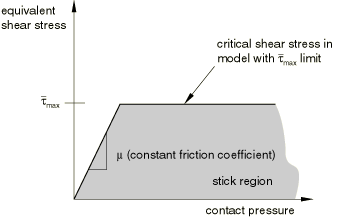
This shear stress limit is typically introduced in cases when the contact pressure stress may become very large (as can happen in some manufacturing processes), causing the Coulomb theory to provide a critical shear stress at the interface that exceeds the yield stress in the material beneath the contact surface. A reasonable upper bound estimate for is , where is the Mises yield stress of the material adjacent to the surface; however, empirical data are the best source for .
Input File Usage
FRICTION, TAUMAX=
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Penalty or Lagrange Multiplier: Shear Stress, Shear stress limit: Specify:
Limitations with the shear stress limit
In Abaqus/Explicit a shear stress limit cannot be used when a contact pair uses a node-based surface as one of the surfaces.
![]()
Anisotropic friction with directional preference as a surface property
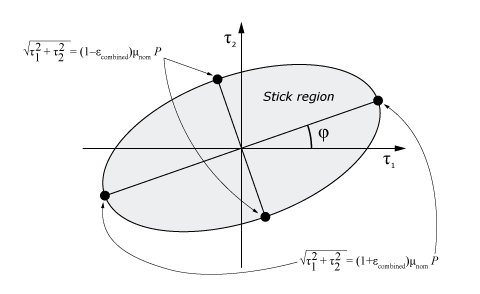
You can specify an anisotropic friction model in Abaqus/Explicit for which directional preferences are specified as surface properties, while the nominal, or average, friction coefficient is specified as a contact interaction property in the same manner as for isotropic friction. The resulting critical contact shear stress surface is elliptical in the – plane, as shown in Figure 5. Points on the critical shear stress surface satisfy the equation:
where represents the combined effects of surface-based directional preferences (and these combined effects evolve as the relative surface orientations change), is the specified nominal (average) friction coefficient, and is the contact pressure. Maximum and minimum values of , corresponding to directions along the major and minor axes of the critical shear stress surface, are and .
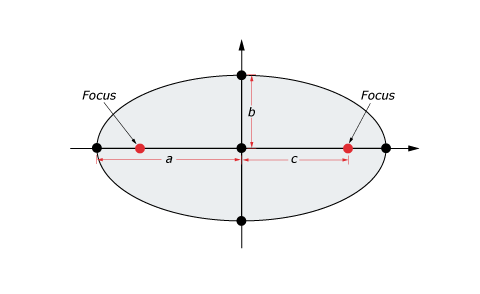
is the frictional directional preference factor. It is a unitless parameter that can range from –1.0 to 1.0 and is a measure of the eccentricity of the scaling ellipse. The most commonly used eccentricity measure for ellipses is (see Figure 6). The relationship between and is:
The critical contact shear stress surface influences the friction algorithm as follows:
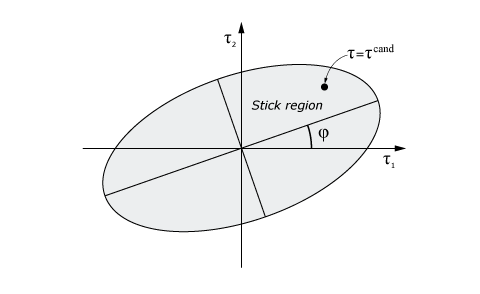
- Abaqus/Explicit computes a candidate contact shear stress necessary to enforce stick conditions:
- If
lies on or within the critical shear stress surface, as shown in
Figure 7,
Abaqus/Explicit
accepts the candidate contact shear stress as the current contact shear stress,
such that stick conditions are in effect.
Figure 7. Example of candidate contact shear stress within the sticking region for anisotropic friction.
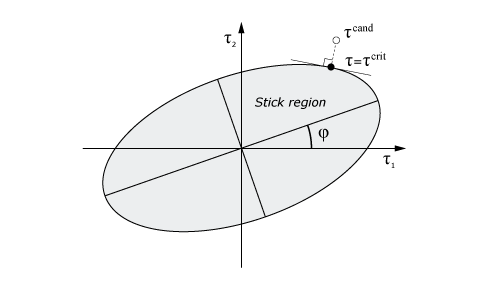
- Otherwise, if
lies outside the critical shear stress surface,
Abaqus/Explicit
sets the contact shear stress equal to
on the critical shear stress surface where the normal to the critical shear
stress surface passes through ,
as shown in
Figure 8,
and sets the direction of incremental slip to be normal to the critical shear
stress surface.
Figure 8. Example of candidate contact shear stress outside of the sticking region for anisotropic friction.
can be thought of as a scaling ellipse calculated as a weighted average of surface-based scaling ellipses:
where the weight factors sum to unity (). and are scaling ellipses representing directional preferences of respective surfaces at a contact location. The maximum and minimum principal values of each scaling ellipse are of the form and , respectively. A lack of directional preference corresponds to .
If both surfaces of a contact interaction contribute directional preference to the frictional behavior, the shape of the scaling ellipse evolves as the (relative) orientations of the contacting surfaces change. For example, for contact between like surfaces with equal weighting factors ():
where and is the angle between major axes of the surface scaling ellipses across the contact interface. Consider the following specific cases for contact between like surfaces:
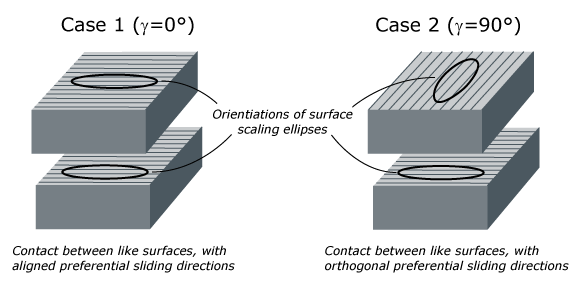
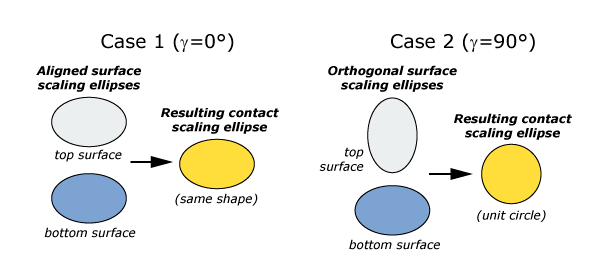
- : This corresponds to aligned directional preferences of contacting surfaces, as shown in Case 1 of Figure 9 and Figure 10. In this situation and .
- : This corresponds to orthogonal directional preferences of contacting surfaces, as shown in Case 2 of Figure 9 and Figure 10. In this situation opposing direction preferences of the surfaces cancel each other, such that and corresponds to a unit circle.
- : and the major axis of bisects the major axes of the respective surface scaling ellipses).
Input File Usage
Use the following option to specify the nominal friction coefficient for an anisotropic friction model with surface-based directional preferences:
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY
Use the following options to specify the surface-based directional preferences and the frictional directional preference factor:
SURFACE PROPERTY ASSIGNMENT, PROPERTY=ORIENTATION FRICTION, DEPENDENCIES=n , , p, ,
Weighting methods for combining preferential direction effects of surfaces for anisotropic friction
Abaqus/Explicit provides three options for computing weight factors for determination of . for all cases with . For cases with , is established according to one of the following three weighting methods (and ):
- Balanced weighting, in which .
- -proportional weighting, in which .
- Maximum--dominant weighting, in which if and if .
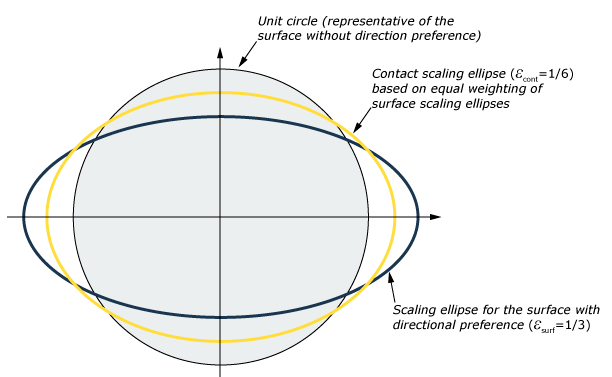
Consider a contact interaction in which only one surface introduces directional preference, with and . In this case balanced weighting leads to , as shown in Figure 11. The other two weighing methods lead to and for this example, in which case the combined scaling ellipse is identical to the scaling ellipse for the surface with directional preference and .
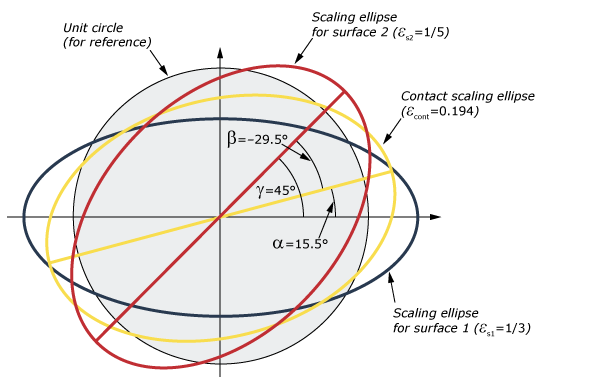
The effect of balanced weighting for a situation with and with a angle between major axes of the surface scaling ellipses is represented in Figure 12. Weight factors for this combination of surface scaling ellipses according to the different weighting methods are:
- With balanced weighting: and .
- With -proportional weighting: and . With this weighting, the contact scaling ellipse would be closer to the scaling ellipse for surface 1 than the contact scaling ellipse for balanced weighting.
- With maximum--dominant weighting: and . With this weighting, the contact scaling ellipse would be identical to the scaling ellipse for surface 1.
Input File Usage
Use the following option to specify the balanced weighting method for combining surface-based directional preferences for the anisotropic friction model:
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY, WEIGHT=BALANCED
Use the following option to specify the epsilon-proportional weighting method for combining surface-based directional preferences for the anisotropic friction model:
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY, WEIGHT=PROPORTIONAL
Use the following option to specify the maximum-epsilon-dominant weighting method for combining surface-based directional preferences for the anisotropic friction model:
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY, WEIGHT=DOMINANT
Defining the friction coefficient
As explained, the critical shear stress surface is proportional to the average, or nominal, friction coefficient. For convenience, you can also specify the minimum or maximum friction coefficient rather than the average one. Internally the value will be converted to the average friction coefficient using the following formulas:
Input File Usage
Use the following option to specify the average friction coefficient (default):
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY, NOMINAL=AVERAGE
Use the following option to specify the minimum friction coefficient:
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY, NOMINAL=MINIMUM
Use the following option to specify the maximum friction coefficient:
FRICTION, ANISOTROPIC BEHAVIOR=SURFACE PROPERTY, NOMINAL=MAXIMUM
Measure of the eccentricity of the scaling ellipse
The measure of eccentricity of the scaling ellipse for each surface is defined using the frictional directional preference factor . Sometimes it is useful to specify the scaling ellipse using the ratio of the friction coefficients:
The relationship between and is given by the following formula:
Input File Usage
To specify the frictional directional preference factor (default):
SURFACE PROPERTY ASSIGNMENT, PROPERTY=ORIENTATION, FRICTION ANISOTROPY=EPSILON
To specify the ratio of the friction cofficients :
SURFACE PROPERTY ASSIGNMENT, PROPERTY=ORIENTATION, FRICTION ANISOTROPY=RATIO
Output of the preferred directions
The preferred local directions for each surface in contact can be output by requesting the generic output variable CORIENT (with the respective vector components CORIENT1 and CORIENT2).
![]()
Anisotropic friction with directional preference associated with contact orientation
Directional preference for this anisotropic friction model is specified as a contact property and is implicitly associated with one surface of a contact interaction. This friction model is available in Abaqus/Standard and is less general than the anisotropic friction model discussed in Anisotropic friction with directional preference as a surface property, which allows both surfaces of a contact interaction to contribute directional preference characteristics.
If you indicate that this anisotropic friction model should be used, you must specify two friction coefficients, where is the coefficient of friction in the first local tangent direction and is the coefficient of friction in the second local tangent direction. The critical contact shear stress surface for this friction model (see Figure 13) is elliptical in the – plane, like the anisotropic friction model discussed in Anisotropic friction with directional preference as a surface property. The shape of the critical contact shear stress surface remains constant in this case, with the extreme points being and .
The orientation of the critical contact shear stress for this friction model evolves with the local tangent directions of the contact interaction, which are discussed in Local tangent directions on a surface. For example, local tangent directions for the finite-sliding, surface-to-surface contact formulation are established from, and evolve with, the slave surface of the contact interaction, so, in this example, directional preference for this anisotropic friction model would evolve with the orientation of the slave surface (and would be independent of the master surface).
The size of the critical-shear-stress ellipse will change with the change in contact pressure between the surfaces. The direction of slip, , is orthogonal to the critical shear stress surface.
The optional equivalent shear stress limit, is applied to the scaled equivalent shear stress, , for anisotropic friction. See Anisotropic friction for the definition and discussion of .
The friction coefficients can depend on slip rate, contact pressure, temperature, and field variables. By default, it is assumed that the friction coefficients do not depend on field variables.
Input File Usage
FRICTION, ANISOTROPIC BEHAVIOR=LEGACY, DEPENDENCIES=n , , , p, ,
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Penalty: Friction, Directionality: Anisotropic
If necessary, toggle on Use slip-rate-dependent data, Use contact-pressure-dependent data, and/or Use temperature-dependent data; and/or specify the Number of field variable dependencies in addition to slip rate, contact pressure, and temperature.
![]()
Preventing slipping regardless of contact pressure
Abaqus offers the option of specifying an infinite coefficient of friction (). This type of surface interaction is called “rough” friction, and with it all relative sliding motion between two contacting surfaces is prevented (except for the possibility of “elastic slip” associated with penalty enforcement) as long as the corresponding normal-direction contact constraints are active. In most cases Abaqus/Standard uses a penalty method to enforce these tangential constraints; however, a Lagrange multiplier method is used during general (non-perturbation) analysis steps if the corresponding normal-direction constraints have directly enforced “hard contact” or exponential pressure-overclosure behavior. Abaqus/Explicit uses either a kinematic or penalty method, depending on the contact formulation chosen.
Rough friction is intended for nonintermittent contact; once surfaces close and undergo rough friction, they should remain closed. Convergence difficulties may arise in Abaqus/Standard if a closed contact interface with rough friction opens, especially if large shear stresses have developed. The rough friction model is typically used in conjunction with the no separation contact pressure-overclosure relationship for motions normal to the surfaces (see Using the no separation relationship), which prohibits separation of the surfaces once they are closed.
When rough friction is used with the no separation relationship for hard contact in Abaqus/Explicit specified with the kinematic contact method, no relative motions of the surfaces will occur. For hard contact in Abaqus/Explicit specified with the penalty contact method, relative motions will be limited to the elastic slip and penetration corresponding to the inexact satisfaction of the contact constraints by the applied penalty forces. When softened tangential behavior is specified in Abaqus/Explicit (see Defining tangential softening in Abaqus/Explicit below), the relative surface motions will be governed by the specified softening behavior.
Input File Usage
FRICTION, ROUGH
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Rough
![]()
Shear stress versus elastic slip while sticking
In some cases some incremental slip may occur even though the friction model determines that the current frictional state is “sticking.” In other words, the slope of the shear (frictional) stress versus total slip relationship may be finite while in the “sticking” state, as shown in Figure 14.
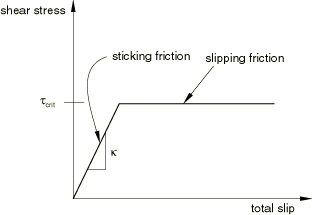
The relationship shown in this figure is analogous to elastic-plastic material behavior without hardening: corresponds to Young's modulus, and corresponds to yield stress; sticking friction corresponds to the elastic regime, and slipping friction corresponds to the plastic regime. A finite value of the sticking stiffness may reflect a user-specified physical behavior or may be characteristic of the constraint enforcement method.
Frictional constraints are enforced with a stiffness (penalty method) by default in Abaqus/Standard and for the general contact algorithm in Abaqus/Explicit; in this case the sticking stiffness will have a finite value. An infinite sticking stiffness, in which case the elastic slip is always zero, can be achieved with the optional Lagrange multiplier method for imposing frictional constraints in Abaqus/Standard or with the kinematic constraint method (available only for contact pairs) in Abaqus/Explicit. In Abaqus/Explicit some tangential contact damping acts on the elastic slip rate by default, as discussed in Contact damping. Tangential softening to reflect a physical behavior is available only in Abaqus/Explicit.
Defining tangential softening in Abaqus/Explicit
To activate softened tangential behavior in Abaqus/Explicit, specify the slope of the shear stress versus elastic slip relationship ( in Figure 14). User subroutine VFRIC cannot be used in conjunction with softened tangential behavior.
Input File Usage
FRICTION, SHEAR TRACTION SLOPE=
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Penalty or Static-Kinetic Exponential Decay: Elastic Slip, Specify:
Stiffness method for imposing frictional constraints in Abaqus/Standard
The stiffness method used for friction in Abaqus/Standard is a penalty method that permits some relative motion of the surfaces (an “elastic slip”) when they should be sticking (similar to the allowable elastic slip defined with softened tangential behavior in Abaqus/Explicit). While the surfaces are sticking (i.e., for the basic isotropic Coulomb friction), the magnitude of sliding is limited to this elastic slip. Abaqus continually adjusts the magnitude of the penalty constraint to enforce this condition.
The stiffness method in Abaqus/Standard requires the selection of an allowable elastic slip, . Using a large in the simulation makes convergence of the solution more rapid at the expense of solution accuracy (there is greater relative motion of the surfaces when they should be sticking). Behavior in which no slip is permitted in the sticking state is approximated more accurately by allowing only a small . If is chosen very small, convergence problems may occur; in that case, it may be better to use the Lagrange multiplier method to apply the sticking constraint (see Lagrange multiplier method for imposing frictional constraints in Abaqus/Standard later in this section).
The default value of allowable elastic slip used by Abaqus/Standard generally works very well, providing a conservative balance between efficiency and accuracy. Abaqus/Standard calculates as a small fraction of the “characteristic contact surface length,” , and scans all of the facets of all the slave surfaces when calculating . Abaqus/Standard reports the value of used for each contact pair in the data (.dat) file if you request detailed printout of contact constraint information (see Controlling the amount of analysis input file processor information written to the data file). The allowable elastic slip is given as , where is the slip tolerance; the default value of is 0.005.
This method of calculating the allowable elastic slip is used for all analysis procedures in Abaqus/Standard except steady-state transport analysis (Steady-state transport analysis), in which the penalty constraint is based on a maximum allowable slip rate, . The maximum slip rate is calculated as
where is the angular spinning rate and R is the radius of the rolling structure.
If the stiffness method is used for an anisotropic friction model, is a nominal allowable elastic slip (or slip rate). If and represent components of elastic slip in the and tangent directions, respectively, the transition from stick to slip will occur when , where is computed as
For example, if , the stick/slip transition will occur at . Depending on values of and , this can be greater or smaller than . As another example, if the “1” and “2” components of elastic slip are equal, the stick/slip transition will occur at , such that the magnitude of the elastic slip, .
Cases in which the default elastic slip value may not be suitable
In certain situations the default value for the allowable elastic slip may not be suitable. For example, slave surfaces defined by node-based surfaces or some contact element types, such as GAPUNI elements, have no physical dimensions and Abaqus/Standard cannot estimate a value of . For models containing only node-based surfaces or these types of contact elements, Abaqus/Standard first tries to use the “characteristic contact surface length” of the other contact pairs in the model. If there are none, it calculates using all of the elements in the model and issues a warning message. If a model contains no elements for which a characteristic length can be determined (for example, if it contains only substructures), Abaqus/Standard has no information with which to calculate . As a result, it uses a value of 1.0 and issues a warning message. If the contact surface face dimensions vary greatly, the average value of may be unreasonable for some contact surfaces. The elastic slip should then be specified directly for the surfaces with a much smaller “characteristic face dimension.”
There are two methods for modifying the allowable elastic slip. One method is to specify directly; the other is to specify the slip tolerance, . Some analyses call for nondefault or only in specific steps (see Changing friction properties during an Abaqus/Standard analysis above).
Specifying the allowable elastic slip directly
You can provide the absolute magnitude of directly. Specify a reasonable value for the relative displacement that may occur before surfaces actually begin to slip. Typically, the allowable elastic slip is set to a small fraction (10−2–10−4) of a “characteristic contact surface face dimension.” In a steady-state transport analysis you can define the maximum allowable viscous slip rate, .
The specified allowable elastic slip will be used only for the contact pairs referencing the contact property definition that contains the friction definition. For example, three surfaces ASURF, BSURF, and CSURF form two contact pairs that each refer to their own contact property definition, as shown below.
| Contact Pair | Contact Property | |
|---|---|---|
| ASURF, BSURF | DEFAULT | |
| CSURF, BSURF | NONDEF | 0.1 |
In the DEFAULT contact property definition no value for is specified, so the allowable elastic slip used for the friction interaction between ASURF and BSURF would be the default value . In the NONDEF contact property definition a value of 0.1 is specified for , which will be the allowable elastic slip used for the friction interaction between CSURF and BSURF.
Input File Usage
FRICTION, ELASTIC SLIP=
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Penalty or Static-Kinetic Exponential Decay: Elastic Slip, Absolute distance:
Changing the default slip tolerance
You can alter the default value of the slip tolerance, . This method of altering the default elastic slip is convenient if the goal is to increase computational efficiency, in which case a value larger than the default of 0.005 would be given, or if the goal is to increase accuracy, in which case a value smaller than the default would be given.
Input File Usage
FRICTION, SLIP TOLERANCE=
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Penalty or Static-Kinetic Exponential Decay: Elastic Slip, Fraction of characteristic surface dimension:
Stiffness method for imposing frictional constraints in Abaqus/Explicit
The stiffness method used for friction with the general contact algorithm in Abaqus/Explicit and, optionally, with the contact pair method in Abaqus/Explicit is a penalty method that permits some relative motion of the surfaces (an “elastic slip”) when they should be sticking (similar to the allowable elastic slip defined with softened tangential behavior in Abaqus/Explicit). While the surfaces are sticking (i.e., ), the magnitude of sliding is limited to this elastic slip. Abaqus continually adjusts the magnitude of the penalty constraint to enforce this condition.
In Abaqus/Explicit you can choose to have contact constraints for the contact pair algorithm enforced with the penalty method; the general contact algorithm always uses a penalty method (see Contact constraint enforcement methods in Abaqus/Explicit).
The default penalty stiffness for frictional constraints is chosen automatically by Abaqus/Explicit and is the same as would be used for normal hard contact constraints. Softening in the normal direction does not affect the penalty stiffness used to enforce stick conditions. If tangential softening is specified (see Defining tangential softening in Abaqus/Explicit above), the penalty stiffness will be equal to the value specified for the slope of the shear stress versus elastic slip relationship. You can specify a scale factor to adjust the penalty stiffness, as discussed in Contact controls for general contact in Abaqus/Explicit and Contact controls for contact pairs in Abaqus/Explicit.
Lagrange multiplier method for imposing frictional constraints in Abaqus/Standard
In Abaqus/Standard the sticking constraints at an interface between two surfaces can be enforced exactly by using the Lagrange multiplier implementation. With this method there is no relative motion between two closed surfaces until . However, the Lagrange multipliers increase the computational cost of the analysis by adding more degrees of freedom to the model and often by increasing the number of iterations required to obtain a converged solution. The Lagrange multiplier formulation may even prevent convergence of the solution, especially if many points are iterating between sticking and slipping conditions. This effect can occur particularly if locally there is a strong interaction between slipping/sticking conditions and contact stresses.
Because of the added cost of using the Lagrange friction formulation, it should be used only in problems where the resolution of the stick/slip behavior is of utmost importance, such as modeling fretting between two bodies. In typical metal forming applications or for contact of rubber components, accurate resolution of the stick/slip behavior is not important enough to justify the added costs of the Lagrange multiplier formulation.
Input File Usage
FRICTION, LAGRANGE
Abaqus/CAE Usage
Interaction module: contact property editor: : Friction formulation: Lagrange Multiplier
Kinematic method for imposing frictional constraints in Abaqus/Explicit
By default, the contact pair algorithm in Abaqus/Explicit uses a kinematic method for imposing frictional constraints (see Contact constraint enforcement methods in Abaqus/Explicit). The kinematic method applies sticking constraints in a way similar to the optional Lagrange multiplier method in Abaqus/Standard; however, the algorithm is quite different. The value of the force required to enforce sticking at a node is first calculated using the mass associated with the node; the distance the node has slipped; the time increment; and additionally for softened contact, the current value of the elastic slip and the elastic slip versus shear stress slope. For hard contact this sticking force is that which is required to maintain the node's position on the opposite surface in the predicted configuration. For softened contact this force is consistent with the user-specified value for the slope of the shear stress versus elastic slip relationship. The sticking force for each node is calculated using the mass associated with the node, the distance the node has slipped, the shear traction-elastic slip slope (if softened contact is specified in the tangential direction), and the time increment. If the shear stress at the node calculated using this force is less than , the node is considered to be sticking and this force is applied to each surface in opposing directions. If the shear stress exceeds , the surfaces are slipping and the force corresponding to is applied. In either case the forces result in acceleration corrections tangential to the surface at the slave node and either the nodes of the master surface facet or the points on the analytical rigid surface that it contacts.
![]()
User-defined friction model
You can define the shear stress between contacting surfaces through a user subroutine when the friction behavior provided by Abaqus is not sufficient. The shear stress can be defined as a function of a number of variables such as slip, slip rate, temperature, and field variables. You can also introduce a number of solution-dependent state variables that you can update and use within the friction user subroutines. You can declare a number of properties or constants associated with your friction model and use these values in the user subroutine.
In addition to the friction user subroutines, subroutines are available for defining the complete mechanical interaction between surfaces, including the interaction in the normal direction as well as the frictional behavior in the tangential direction; see User-defined interfacial constitutive behavior for more information.
Defining generic frictional behavior
You can define a generic frictional behavior between contacting surfaces using user subroutine FRIC in Abaqus/Standard. In Abaqus/Explicit the generic frictional behavior for contact pairs is defined in user subroutine VFRIC, while the generic frictional behavior for general contact is defined in user subroutine VFRICTION.
Input File Usage
Use the following option to define a frictional behavior with user subroutine FRIC or VFRIC:
FRICTION, USER, DEPVAR=n, PROPERTIES=p
Use the following option to define a frictional behavior with user subroutine VFRICTION:
FRICTION, USER=FRICTION, DEPVAR=n, PROPERTIES=p
Abaqus/CAE Usage
Use the following options to define a frictional behavior with user subroutine FRIC or VFRIC:
Interaction module: contact property editor: : Friction formulation: User-defined, Number of state-dependent variables: n, Friction Properties
User subroutine VFRICTION is not supported in Abaqus/CAE.
Defining complex isotropic friction
Abaqus provides a simple way to specify complex isotropic frictional behavior when the expression for the friction coefficient can be defined explicitly. You need only to specify the friction coefficient, and Abaqus will compute the resulting frictional forces. Abaqus/Standard provides user subroutine FRIC_COEF and Abaqus/Explicit provides user subroutine VFRIC_COEF for this purpose. VFRIC_COEF can be used only with general contact.
Input File Usage
FRICTION, USER=COEFFICIENT, PROPERTIES=p
Abaqus/CAE Usage
User subroutines FRIC_COEF and VFRIC_COEF are not supported in Abaqus/CAE.
![]()
Consideration of incremental rotation of shell and beam thickness offsets in Abaqus/Explicit
By default, in Abaqus/Explicit slip increment calculations for friction do not account for the incremental rotation of shell and beam thickness offsets, and frictional constraints do not apply a moment to nodes offset from the contact interface due to shell or beam thicknesses. This behavior can be modified for general contact; for details see Consideration of incremental rotation of shell and beam thickness offsets for frictional contact.
![]()
Improving Abaqus/Standard simulations that include friction in the surface interactions
Several features of the frictional interaction of surfaces can have a strong influence on the rate of convergence in an Abaqus/Standard simulation.
Unsymmetric terms in the system of equations
Friction constraints produce unsymmetric terms when the surfaces are sliding relative to each other. These terms have a strong effect on the convergence rate if frictional stresses have a substantial influence on the overall displacement field and the magnitude of the frictional stresses is highly solution dependent. Abaqus/Standard will automatically use the unsymmetric solution scheme if or if is pressure-dependent. If desired, you can turn off the unsymmetric solution scheme; see Matrix storage and solution scheme in Abaqus/Standard.
No slip occurs with rough friction; the contribution to the stiffness will be fully symmetric, and Abaqus/Standard will use the symmetric solution scheme by default.
![]()
Heat generated by frictional interaction of surfaces
In fully coupled temperature-displacement analysis and fully coupled thermal-electrical-structural analysis, all dissipated mechanical (frictional) energy is converted to heat and distributed equally between the two surfaces by default. This behavior can be modified; for details about this and other thermal surface interactions, see Thermal contact properties.
![]()
Temperature and field-variable dependence of friction properties for structural elements
Temperature and field-variable distributions in beam and shell elements can generally include gradients through the cross-section of the element. Contact between these elements occurs at the reference surface; therefore, temperature and field-variable gradients in the element are not considered when determining friction properties that depend on these variables.
![]()
Surface interaction variables related to friction
Abaqus provides output of the shear stresses at points on the slave surface that use a surface interaction model containing frictional properties. The shear stresses, CSHEAR1 and CSHEAR2, are given in the two orthogonal local tangent directions, which are constructed on the master surface (see Contact formulations in Abaqus/Standard). There is only one local tangent direction in two-dimensional problems. Details about how to request contact surface variable output are given in About contact pairs in Abaqus/Standard and About contact pairs in Abaqus/Explicit.
Contour plots of these variables can also be plotted in Abaqus/CAE.
![]()
References
- “Models and Computational Methods for Dynamic Friction Phenomena,” Computer Methods in Applied Mechanics and Engineering, vol. 52, pp. 527–634, 1985.