VFRIC | ||||||||
|
| |||||||
ProductsAbaqus/Explicit
Terminology
The use of user subroutine VFRIC requires familiarity with the following terminology.
Surface node numbers
The “surface node number” refers to the position of a particular node in the list of nodes on the surface. For example, there are nSlvNod nodes on the slave surface. Number nSlvNod, is the surface node number of the nth node in this list; jSlvUid is the user-defined global number of this node. An Abaqus/Explicit model can be defined in terms of an assembly of part instances (see Assembly definition). In such models a node number in jSlvUid is an internally generated node number. If the original node number and part instance name are required, call the utility routine VGETPARTINFO (see Obtaining part information).
Contact points
The nodes on the slave surface that are in contact in the current time increment are defined as “contact points.” The number of contact points is passed into this subroutine as nContact. The array jConSlvid(nContact) gives the surface node numbers for the contact points.
![]()
Local coordinate system
A local coordinate system is defined for each contact point to facilitate specification of frictional forces and incremental slips. The local 1-direction for both two-dimensional and three-dimensional contact is tangential to the master surface, and it is defined by , where is the incremental slip vector. The incremental slip vector used to define corresponds to the incremental slip in the current time increment for penalty contact and the predicted incremental slip for kinematic contact. The master surface normal direction, , is the local 2-direction for two-dimensional contact and the local 3-direction for three-dimensional contact. The local 2-direction for three-dimensional contact is given by , which is also tangent to the master surface. The vectors are shown in Figure 1 and Figure 2. The direction cosines for and with respect to the global coordinate system are available in dirCosT1 and dirCosN, respectively. In the case of zero incremental slip () we choose an arbitrary direction for that is orthogonal to the normal direction, .
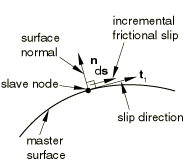
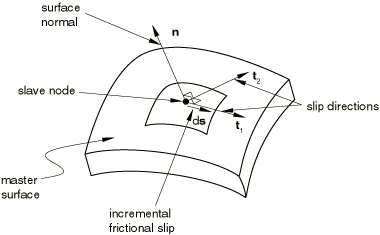
![]()
Frictional forces
You specify the frictional force, fTangential, at each contact point in local coordinates in this subroutine. The array fTangential is dimensioned such that only the tangential components can be specified. Any components of the frictional force that are not specified will remain equal to zero. For three-dimensional contact with isotropic friction, only the first component of the frictional force need be specified since the second component should be zero. A “stick force” at each contact point is provided in the array fStickForce to assist you in setting the appropriate frictional force values. The stick force is the force required to prevent additional “plastic” slipping. The stick force at each contact point is provided as a scalar value as it would act in the direction opposite to . The stick force is computed prior to calling user subroutine VFRIC by either the kinematic or the penalty contact algorithm. See Contact constraint enforcement methods in Abaqus/Explicit for descriptions of the kinematic and penalty contact algorithms and the user interface for choosing between them. The first component of the frictional force should be in the range between zero and minus the stick force value. Typically, the stick force will be positive and the first component of the applied frictional force will be negative, opposing the incremental slip. Penalty contact includes an elastic slip regime due to finite penalty stiffness, so occasionally, during recovery of elastic slip, the stick force will be negative, indicating that it is appropriate for the first component of the frictional force to be positive (i.e., acting in the same direction as the incremental slip). A noisy or unstable solution is likely to result if the first component of fTangential is set outside of the range between zero and negative the value of the stick force.
After user subroutine VFRIC is called, frictional forces that oppose the forces specified at the contact points are distributed to the master nodes. For balanced master-slave contact we then compute weighted averages of the frictional forces for both master-slave orientations. These forces are directly applied if the penalty contact algorithm is being used. If the kinematic contact algorithm is being used, the frictional forces are converted to acceleration corrections by dividing by the nodal masses.
![]()
User subroutine interface
subroutine vfric(
C Write only -
1 fTangential,
C Read/Write -
2 statev,
C Read only -
3 kStep, kInc, nContact, nFacNod, nSlvNod, nMstNod,
4 nFricDir, nDir, nStateVar, nProps, nTemp, nPred, numDefTfv,
5 jSlvUid,jMstUid, jConSlvid, jConMstid, timStep, timGlb,
6 dTimCur, surfInt, surfSlv, surfMst, lContType,
7 dSlipFric, fStickForce, fTangPrev, fNormal, frictionWork,
8 shape, coordSlv, coordMst, dirCosSl, dircosN, props,
9 areaSlv, tempSlv, preDefSlv, tempMst, preDefMst)
C
include `vaba_param.inc'
C
character*80 surfInt, surfSlv, surfMst
C
dimension props(nProps), statev(nStateVar,nSlvNod),
1 dSlipFric(nDir,nContact),
2 fTangential(nFricDir,nContact),
3 fTangPrev(nDir,nContact),
4 fStickForce(nContact), areaSlv(nSlvNod),
5 fNormal(nContact), shape(nFacNod,nContact),
6 coordSlv(nDir,nSlvNod), coordMst(nDir,nMstNod),
7 dirCosSl(nDir,nContact), dircosN(nDir,nContact),
8 jSlvUid(nSlvNod), jMstUid(nMstNod),
9 jConSlvid(nContact), jConMstid(nFacNod,nContact)
1 tempSlv(nContact), preDefSlv(nContact,nPred),
2 tempMst(numDefTfv), preDefMst(numDefTfv,nPred)
user coding to define fTangential
and, optionally, statev
return
end![]()
Variables to be defined
- fTangential(nFricDir, nContact)
This array must be updated to the current values of the frictional force components for all contact points in the local tangent directions. See Figure 1 and Figure 2 for definition of the local coordinate system. This array will be zero (no friction force) until you reset it.
![]()
Variables that can be updated
- statev(nstateVar, nSlvNod)
This array contains the user-defined solution-dependent state variables for all the nodes on the slave surface. You define the size of this array (see Frictional behavior for more information). This array will be passed in containing the values of these variables prior to the call to user subroutine VFRIC. If any of the solution-dependent state variables is being used in conjunction with the friction behavior, it must be updated in this subroutine. The state variables are available even for slave nodes that are not in contact. This may be useful when, for example, the state variables need to be reset for slave nodes that are not in contact.
![]()
Variables passed in for information
- kStep
Step number.
- kInc
Increment number.
- nContact
Number of contacting slave nodes.
- nFacNod
Number of nodes on each master surface facet (nFacNod is 2 for two-dimensional surfaces, nFacNod is 4 for three-dimensional surfaces). If the master surface is an analytical rigid surface, this variable is passed in as 0.
- nSlvNod
Number of slave nodes.
- nMstNod
Number of master surface nodes, if the master surface is made up of facets. If the master surface is an analytical rigid surface, this variable is passed in as 0.
- nFricDir
Number of tangent directions at the contact points (nFricDir = nDir - 1).
- nDir
Number of coordinate directions at the contact points. (In a three-dimensional model nDir will be two if the surfaces in the contact pair are two-dimensional analytical rigid surfaces or are formed by two-dimensional elements.)
- nStateVar
Number of user-defined state variables.
- nProps
User-specified number of property values associated with this friction model.
- nTemp
1 if the temperature is defined and 0 if the temperature is not defined.
- nPred
Number of predefined field variables.
- numDefTfv
Equal to nContact if the master surface is made up of facets. If the master surface is an analytical rigid surface, this variable is passed in as 1.
- jSlvUid(nSlvNod)
This array lists the user-defined global node numbers (or internal node numbers for models defined in terms of an assembly of part instances) of the nodes on the slave surface.
- jMstUid(nMstNod)
This array lists the user-defined global node numbers (or internal node numbers for models defined in terms of an assembly of part instances) of the nodes on the master surface. If the master surface is an analytical rigid surface, this array is passed in as a dummy array.
- jConSlvid(nContact)
This array lists the surface node numbers of the slave surface nodes that are in contact.
- jConMstid(nFacNod, nContact)
This array lists the surface node numbers of the master surface nodes that make up the facet with which each contact point is in contact. If the master surface is an analytical rigid surface, this array is passed in as a dummy array.
- timStep
Value of step time.
- timGlb
Value of total time.
- dtimCur
Current increment in time from to .
- surfInt
User-specified surface interaction name, left justified.
- surfSlv
Slave surface name.
- surfMst
Master surface name.
- lContType
Contact type flag. This flag is set based on the type of constraint enforcement method (see Contact constraint enforcement methods in Abaqus/Explicit) being used: 1 for kinematic contact and 2 for penalty contact. Stick conditions are satisfied exactly with the kinematic contact algorithm; they are satisfied only approximately (subject to an automatically chosen penalty stiffness value) with the penalty contact algorithm.
- dSlipFric(nDir, nContact)
This array contains the incremental frictional slip during the current time increment for each contact point in the current local coordinate system. These incremental slips correspond to tangential motion in the time increment from to . For penalty contact this incremental slip is used to define the local coordinate system at each contact point (see Figure 1 and Figure 2) so that only the first component of dSlipFric can be nonzero in the local system. The contact points for kinematic contact are determined based on penetrations detected in the predicted configuration (at ), and the predicted incremental slip direction is used to define the local coordinate system at each contact point. If the slip direction changes between increments, dSlipFric may have a nonzero component in the local 2-direction and, if the surface is faceted and the contact point moves from one facet to another, in the local 3-direction.
- fStickForce(nContact)
This array contains the magnitude of frictional force required to enforce stick conditions at each contact point. For kinematic contact this force corresponds to no slip; for penalty contact this force depends on the previous frictional force, the value of the penalty stiffness, and the previous incremental slip. The penalty stiffness is assigned automatically. Occasionally, during recovery of elastic slip associated with the penalty method, the stick force will be assigned a negative value.
- fTangPrev(nDir, nContact)
This array contains the values of the frictional force components calculated in the previous increment but provided in the current local coordinate system (zero for nodes that were not in contact).
- fNormal(nContact)
This array contains the magnitude of the normal force for the contact points applied at the end of current time increment; i.e., at time .
- frictionWork
This variable contains the value of the total frictional dissipation in the entire model from the beginning of the analysis. The units are energy per unit area.
- shape(nFacNod, nContact)
For each contact point this array contains the shape functions of the nodes of its master surface facet, evaluated at the location of the contact point. If the master surface is an analytical rigid surface, this array is passed in as a dummy array.
- coordSlv(nDir, nSlvNod)
Array containing the nDir components of the current coordinates of the slave nodes.
- coordMst(nDir, nMstNod)
Array containing the nDir components of the current coordinates of the master nodes. If the master surface is an analytical rigid surface, this array is passed in as a dummy array.
- dirCosSl(nDir, nContact)
Direction cosines of the incremental slip at the contact points.
- dircosN(nDir, nContact)
Direction cosines of the normals to the master surface at the contact points.
- props(nProps)
User-specified vector of property values to define the frictional behavior between the contacting surfaces.
- areaSlv(nSlvNod)
Area associated with the slave nodes (equal to 1 for node-based surface nodes).
- tempSlv(nContact)
Current temperature at the slave nodes.
- preDefSlv(nContact,nPred)
Current user-specified predefined field variables at the slave nodes (initial values at the beginning of the analysis and current values during the analysis).
- tempMst(numDefTfv)
Current temperature at the nearest points on the master surface.
- preDefMst(numDefTfv,nPred)
Current user-specified predefined field variables at the nearest points on the master surface (initial values at the beginning of the analysis and current values during the analysis).