Axisymmetric shell elements with nonlinear, asymmetric deformation

This section provides a reference to the axisymmetric shell elements with nonlinear, asymmetric deformation available in Abaqus/Standard. For an axisymmetric reference geometry where axisymmetric deformation is expected, use regular axisymmetric elements (see Axisymmetric shell element library). For an axisymmetric reference geometry where nonaxisymmetric deformation is expected and the thickness to characteristic radius is high or through the thickness detail is required, use CAXA-type elements (see Axisymmetric solid elements with nonlinear, asymmetric deformation).

Conventions
Element types
Nodal coordinates required
Element property definition
Element-based loading
Element output
Node ordering on elements

Conventions

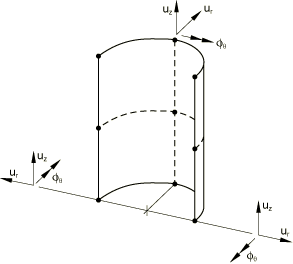
Coordinate 1 is r, coordinate 2 is z. The r-direction corresponds to the global X-direction in the $θ = 0^{\circ}$ plane and the global Y-direction in the $θ = 90^{\circ}$ plane, and the z-direction corresponds to the global Z-direction. Coordinate 1 should be greater than or equal to zero.

Degree of freedom 1 is $u_{r}$ , degree of freedom 2 is $u_{z}$ , degree of freedom 6 is rotation in the r–z plane.

Even though the symmetry in the r–z plane at $θ = 0, π$ allows the modeling of half of the initially axisymmetric structure, the loading must be specified as the total load on the full axisymmetric body. Consider, for example, a cylindrical shell loaded by a unit uniform axial force. To produce a unit load on a SAXA element with four modes, the nodal forces are 1/8, 1/4, 1/4, 1/4, and 1/8 at $θ = 0$ , $π / 4$ , $π / 2$ , $3 π / 4$ , and $π$ , respectively.

The meridional direction is the direction tangent to the element in the r–z plane; that is, the meridional direction is along the line that is rotated about the axis of symmetry to generate the full three-dimensional body.

The circumferential or hoop direction is the direction normal to the r–z plane.

Element types

SAXA1N: Linear interpolation, Fourier shell element with 2 nodes in the meridional direction and N Fourier modes
SAXA2N: Quadratic interpolation, Fourier shell element with 3 nodes in the meridional direction and N Fourier modes

Active degrees of freedom

1, 2, 6

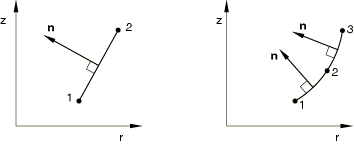
See Figure 1 for the positive nodal displacement and rotation directions. The nodal rotation, $ϕ_{θ}$ , is consistent with the SAX elements; however, a positive nodal rotation is in the negative $θ$ -direction.

Figure 1. Element coordinate system and positive displacement/rotation directions. SAXA22 element shown.

Additional solution variables

SAXA $1 N$ elements have $6 N$ variables relating to ( $u_{θ}$ , $ϕ_{r}$ , $ϕ_{z}$ ).

SAXA $2 N$ elements have $9 N$ variables relating to ( $u_{θ}$ , $ϕ_{r}$ , $ϕ_{z}$ ).

Nodal coordinates required

r, z (given in the r–z plane for $θ = 0$ )

The two direction cosines, $N_{r}$ and $N_{z}$ , of the nodal normal field can be specified either in the nodal data or by a user-specified normal definition (see Normal definitions at nodes).

Element property definition

If a general shell section is used and the section stiffness matrix is given directly, a full 6 × 6 section stiffness should be specified (i.e., 21 constants as for a three-dimensional shell).

Input File Usage

Use either of the following options:

SHELL SECTION
SHELL GENERAL SECTION

In addition, use the following option for variable thickness shells:

NODAL THICKNESS

Element-based loading

Distributed loads

Distributed loads are specified as described in Distributed loads.

Distributed load magnitudes are per unit area or per unit volume. They do not need to be multiplied by $2 π$ times the radius.

*dload

Load ID (*DLOAD): BX
FL⁻³
Body force per unit volume in the global X-direction.

Load ID (*DLOAD): BZ
FL⁻³
Body force per unit volume in the global Z-direction.

Load ID (*DLOAD): BXNU
FL⁻³
Nonuniform body force in the global X-direction with magnitude supplied via user subroutine DLOAD.

Load ID (*DLOAD): BZNU
FL⁻³
Nonuniform body force in the global Z-direction with magnitude supplied via user subroutine DLOAD.

Load ID (*DLOAD): HP
FL⁻²
Hydrostatic pressure on the shell surface, linear in the global Z-direction.

Load ID (*DLOAD): P
FL⁻²
Pressure on the shell surface.

Load ID (*DLOAD): PNU
FL⁻²
Nonuniform pressure on the shell surface with magnitude supplied via user subroutine DLOAD.

Element output

The numerical integration with respect to $θ$ employs the trapezoidal rule. There are $2 (N + 1)$ equally spaced integration planes in the element, including the $θ = 0^{\circ}$ and $θ = 180^{\circ}$ planes, with N being the number of Fourier modes. Consequently, the radial nodal forces corresponding to pressure loads applied in the circumferential direction are distributed in this direction in the ratio of $1 : 1$ in the 1 Fourier mode element, $1 : 2 : 1$ in the 2 Fourier mode element, and $1 : 2 : 2 : 2 : 1$ in the 4 Fourier mode element. The sum of these consistent nodal forces is equal to the integral of the applied pressure over the full circumference ( $2 π$ ).

Stress, strain, and other tensor components

Stress and other tensors (including strain tensors) are available for elements with displacement degrees of freedom. All tensors have the same components. For example, the stress components are as follows:

S11: Meridional stress.
S22: Hoop (circumferential) stress.
S12: Local 12 shear stress (zero at $θ = 0^{\circ}$ and $180^{\circ}$ ).

Section forces

SF1: Direct membrane force per unit width in local 1-direction.
SF2: Direct membrane force per unit width in local 2-direction.
SF3: Shear membrane force per unit width in local 1–2 plane.
SF4: Integrated stress in the thickness direction; always zero.
SM1: Bending moment per unit width about local 2-axis.
SM2: Bending moment per unit width about local 1-axis.
SM3: Twisting moment per unit width in local 1–2 plane.

Section strains

SE1: Direct membrane strain in local 1-direction.
SE2: Direct membrane strain in local 2-direction.
SE3: Shear membrane strain in local 1–2 plane.
SE4: Strain in the thickness direction.
SK1: Bending strain in local 1-direction.
SK2: Bending strain in local 2-direction.
SK3: Twisting strain in local 1–2 plane.

The section force and moment resultants per unit length in the normal basis directions for a given layer of thickness h can be defined, in components relative to this basis, as:

\begin{matrix} (SF1, SF2, SF3) & = \int_{- h / 2 - z_{0}}^{h / 2 - z_{0}} (σ_{11}, σ_{22}, σ_{12}) d z, \\ (SM1, SM2, SM3) & = \int_{- h / 2 - z_{0}}^{h / 2 - z_{0}} (σ_{11}, σ_{22}, σ_{12}) z d z, \end{matrix}

where $z_{0}$ is the offset of the reference surface from the midsurface.

The local directions are defined in Defining the initial geometry of conventional shell elements.

Current shell thickness

STH: Current shell thickness.

Node ordering on elements

The node ordering in the first generator plane ( $θ = 0$ ) of each element is shown below. You specify the line or curve of nodes in the generator plane just as with the SAX1 and SAX2 elements. Each element must have N more planes of nodes defined, where N is the number of Fourier modes used. Abaqus/Standard will generate these additional circumferential nodes and number them by adding a constant offset value to the nodes specified in the first plane (see Element definition).