A cracking model for concrete and other brittle materials

A smeared model is chosen to represent the discontinuous macrocrack brittle behavior. In this approach we do not track individual “macro” cracks: rather, the presence of cracks enters into the calculations by the way the cracks affect the stress and material stiffness associated with each material calculation point.

Here, for simplicity, the term “crack” is used to mean a direction in which cracking has been detected at the material calculation point in question. The closest physical concept is that there exists a continuum of microcracks at the point, oriented as determined by the model. The anisotropy introduced by cracking is included in the model since it is assumed to be important in the simulations for which the model is intended.

Some objections have been raised against smeared crack models. The principal concern is that this modeling approach inherently introduces mesh sensitivity in the solutions, in the sense that the finite element results do not converge to a unique result. For example, since cracking is associated with strain softening, mesh refinement will lead to narrower crack bands. Many researchers have addressed this concern, and the general consensus is that Hillerborg's (1976) approach—based on brittle fracture concepts—is adequate to deal with this issue for practical purposes. A length scale, typically in the form of a “characteristic” length, is introduced to “regularize” the smeared continuum models and attenuate the sensitivity of the results to mesh density. This aspect of the model is discussed in detail later.

Various researchers have proposed three basic crack direction models (Rots and Blaauwendraad, 1989): fixed, orthogonal cracks; the rotating crack model; and fixed, multidirectional (nonorthogonal) cracks. In the fixed, orthogonal crack model the direction normal to the first crack is aligned with the direction of maximum tensile principal stress at the time of crack initiation. The model has memory of this crack direction, and subsequent cracks at the point under consideration can only form in directions orthogonal to the first crack. In the rotating crack concept only a single crack can form at any point (aligned with the direction of maximum tensile principal stress). Thus, the single crack direction rotates with the direction of the principal stress axes. This model has no memory of crack direction. Finally, the multidirectional crack model allows the formation of any number of cracks at a point as the direction of the principal stress axes changes with loading. In practice, some limitation is imposed on the number of cracks allowed to form at a point. The model has memory of all crack directions.

The multidirectional crack model is the least popular, mainly because the criterion used to decide when subsequent cracks form (to limit the number of cracks at a point) is somewhat arbitrary: the concept of a “threshold angle” is introduced to prevent new cracks from forming at angles less than this threshold value to existing cracks. The fixed orthogonal and rotating crack models have both been used extensively, even though objections can be raised against both. In the rotating crack model the concept of crack closing and reopening is not well-defined because the orientation of the crack can vary continuously. The fixed orthogonal crack model has been criticized mainly because the traditional treatment of “shear retention” employed in the model tends to make the response of the model too stiff. This problem can be resolved by formulating the shear retention in a way that ensures that the shear stresses tend to zero as deformation on the crack interfaces takes place (this is done in the Abaqus model, as described later). Finally, although the fixed orthogonal crack model has the orthogonality limitation, it is considered superior to the rotating crack model in cases where the effect of multiple cracks is important (the rotating crack model is restricted to a single crack at any point).

The fixed orthogonal cracks model is used in Abaqus so that the maximum number of cracks at a material point is limited by the number of direct stress components present at that material point of the finite element model (for example, a maximum of three cracks in three-dimensional, axisymmetric, and plane strain problems or a maximum of two cracks in plane stress problems). Once cracks exist at a point, the component forms of all vector and tensor valued quantities are rotated so that they lie in the local system defined by the crack orientation vectors (the normals to the crack faces). The model ensures that these crack face normal vectors are orthogonal so that this local system is rectangular Cartesian. Crack closing and reopening can take place along the directions of the crack surface normals. The model neglects any permanent strain associated with cracking; that is, we assume that the cracks can close completely when the stress across them becomes compressive.

The main ingredients of the model are a strain rate decomposition into elastic (concrete) and cracking strain rates, elasticity, a set of cracking conditions, and a cracking relation (the evolution law for the cracking behavior). The main advantage of the strain decomposition is that it allows the eventual addition of other effects, such as plasticity and creep, in a consistent manner. The elastic-cracking strain decomposition also allows the separate identification of a cracking strain that represents the state of a crack; this contrasts with the classical smeared cracking models where a single strain quantity is used to represent the state of a cracked solid in a homogenized form leading to a modified (damaged) elasticity formulation.

We begin with a strain rate decomposition,

where $d\mathit{\epsilon }$ is the total mechanical strain rate, $d{\mathit{\epsilon }}^{el}$ is the elastic strain rate representing the uncracked concrete (the continuum between the cracks), and $d{\mathit{\epsilon }}^{ck}$ is the cracking strain rate associated with any existing cracks.

The strains in Equation 1 are referred to the global Cartesian coordinate system and can be written in vector form (in a three-dimensional setting) as

For incorporating the cracking relations it is convenient to define a local Cartesian coordinate system $n,t,s$ that is aligned with the crack directions. In the local system, shown in Figure 1, the strains are

Figure 1. Global and local cracking coordinate systems.

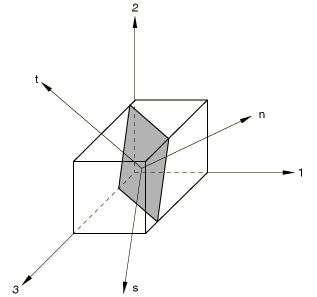
The transformation between global and local strains is written in matrix form as

where $\mathbf{T}$ is a transformation matrix constructed from the direction cosines of the local cracking coordinate system. $\mathbf{T}$ is constant in our fixed crack model.

The conjugate stress quantities can be written in the global coordinate system as

and in the local cracking system as

The transformation between local and global stresses is then

The intact continuum between the cracks is modeled with isotropic, linear elasticity. The orthotropic nature of the cracked material is introduced in the cracking component of the model. As stated earlier, the approach of decomposing the strains into elastic, intact concrete, strains, and cracking strains has the advantage that this smeared model can be generalized to include other effects such as plasticity and creep (although such generalizations are not yet included in Abaqus/Explicit).

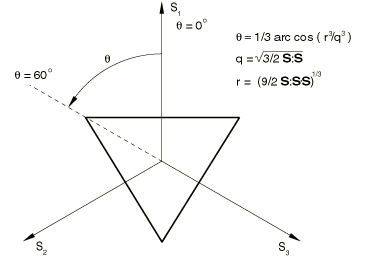
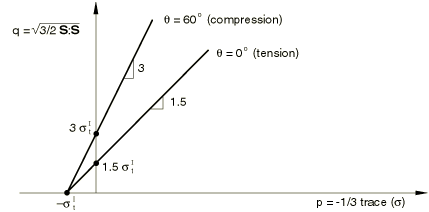
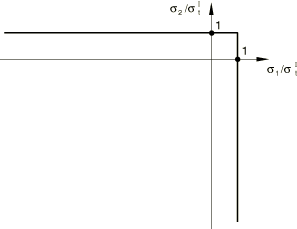
A simple Rankine criterion is used to detect crack initiation. This states that a crack forms when the maximum principal tensile stress exceeds the tensile strength of the brittle material. The Rankine crack detection surface is shown in Figure 2 in the deviatoric plane, in Figure 3 in the meridional plane, and in Figure 4 in plane stress. Although crack detection is based purely on Mode I fracture considerations, ensuing cracked behavior includes both Mode I (tension softening) and Mode II (shear softening/retention) behavior, as described later.

Figure 2. Rankine criterion in the deviatoric plane.

Figure 3. Rankine criterion in the meridional plane.

Figure 4. Rankine criterion in plane stress.

As soon as the Rankine criterion for crack formation has been met, we assume that a first crack has formed. The crack surface is taken to be normal to the direction of the maximum tensile principal stress. Subsequent cracks can form with crack surface normals in the direction of maximum principal tensile stress that is orthogonal to the directions of any existing crack surface normals at the same point.

The crack orientations are stored for subsequent calculations, which are done for convenience in a local coordinate system oriented in the crack directions. Cracking is irrecoverable in the sense that, once a crack has occurred at a point, it remains throughout the rest of the calculation. However, a crack may subsequently close and reopen.

We introduce a consistency condition for cracking (analogous to the yield condition in classical plasticity) written in the crack direction coordinate system in the form of the tensor

where

and ${\mathit{\sigma }}^{I,II}$ represents a tension softening model (Mode I fracture) in the case of the direct components of stress and a shear softening/retention model (Mode II fracture) in the case of the shear components of stress. The matrices $\partial \mathbf{C}/\partial \mathbf{t}$ and $\partial \mathbf{C}/\partial {\mathit{\sigma }}^{I,II}$ are assumed to be diagonal, implying the usual assumption that there is no coupling between cracks in the cracking conditions.

Each cracking condition is more complex than a classical yield condition in the sense that two cracking states are possible (an actively opening crack state and a closing/reopening crack state), contrasting with a single plastic state in classical plasticity. This can be illustrated by writing the cracking conditions for a particular crack normal direction n explicitly:

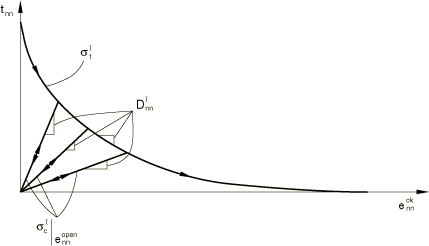
for an actively opening crack, where ${\sigma }_t^I\left(e_{nn}^{ck}\right)$ is the tension softening evolution (defined by the user), and

for a closing/reopening crack, where ${{\sigma }_c^I\left(e_{nn}^{ck}\right)|}_{e_{nn}^{\mathrm{open}}}$ is the crack closing/reopening evolution that depends on the maximum crack opening strain defined as

These conditions are illustrated in Figure 5 and represent the tension softening model adopted for the cracking behavior normal to crack surfaces. Similar conditions can be written for the other two possible crack normal directions, s and t. It must be emphasized that, although the cracking condition of Equation 4 has been written for the most general case of all possible cracks existing, only the components of $\mathbf{C}$ that refer to existing cracks are considered in the computations with this model.

Figure 5. Cracking conditions for Mode I cracking.

The cracking conditions for the shear components in the crack coordinate system are activated when the associated normal directions are cracked. We now present the shear cracking conditions by writing the conditions for shear component $nt$ explicitly.

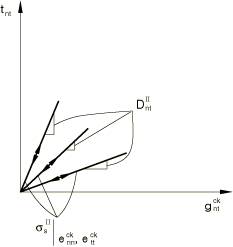
The crack opening dependent shear model (shear retention model) is written as

for shear loading or unloading of the crack, where ${\sigma }_s^{II}\left(g_{nt}^{ck},e_{nn}^{ck},e_{tt}^{ck}\right)$ is the shear evolution that depends linearly on the shear strain and also depends on the crack opening strain (this dependency being defined by the user). Figure 6 illustrates the model. Although this model is inspired by the traditional shear retention models, it differs from those models in one important aspect: the shear stress tends to zero as the crack develops. This is discussed in more detail later.

Figure 6. Cracking conditions for Mode II cracking (crack opening dependent model).

The relation between the local stresses and the cracking strains at the crack interfaces is written in rate form as

where ${\mathbf{D}}^{ck}$ is a diagonal cracking matrix that depends on the state of the existing cracks. The definition of these diagonal components ($D_{nn}^I,D_{tt}^I,D_{ss}^I,D_{nt}^{II},D_{ns}^{II},D_{ts}^{II}$) is given in Figure 5 and Figure 6.

Using the strain rate decomposition (Equation 3) and the elasticity relations, we can write the rate of stress as

where ${\mathbf{D}}^{el}$ is the isotropic linear elasticity matrix.

Premultiplying Equation 9 by ${\mathbf{T}}^T$ and substituting Equation 5 and Equation 8 into the resulting left-hand side yields

Finally, substituting Equation 10 into Equation 9 results in the stress-strain rate equations:

The brittle fracture concept of Hilleborg (1976) forms the basis of the postcracked behavior in the direction normal to the crack surface (commonly referred to as tension softening). We assume that the fracture energy required to form a unit area of crack surface in Mode I, $G_f^I$, is a material property. This value can be calculated from measuring the tensile stress as a function of the crack opening displacement (Figure 7), as

Figure 7. Mode I fracture energy based cracking behavior.

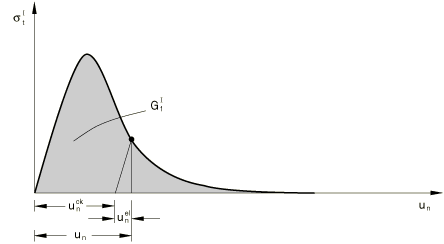
Typical values of $G_f^I$ range from 40 N/m (0.22 lb/in) for a typical construction concrete (with a compressive strength of approximately 20 MPa, 2850 lb/in²) to 120 N/m (0.67 lb/in) for a high strength concrete (with a compressive strength of approximately 40 MPa, 5700 lb/in²).

The implication of assuming that $G_f^I$ is a material property is that, when the elastic part of the displacement, $u_n^{el}$, is eliminated, the relationship between the stress and the remaining part of the displacement, $u_n^{ck}=u_n-u_n^{el}$, is fixed, regardless of the specimen size. For example, consider a specimen developing a single crack across its section as tensile displacement is applied to it: $u_n^{ck}$ is the displacement across the crack and is not changed by using a longer or shorter specimen in the test (so long as the specimen is significantly longer than the width of the crack band, which will typically be of the order of the aggregate size). Thus, this important part of the cracked concrete's tensile behavior is defined in terms of a stress/displacement relationship.

In the finite element implementation of this model we must, therefore, compute the relative displacement at a material point to provide $u_n^{ck}$. We do this in Abaqus by multiplying the strain by a characteristic length associated with the material point (the cracking strain in local crack direction n is used as an example):

where h is the characteristic length. This characteristic crack length is based on the element geometry and formulation: it is a typical length of a line across an element for a first-order element; it is half of the same typical length for a second-order element. For beams and trusses it is a characteristic length along the element axis. For membranes and shells it is a characteristic length in the reference surface. For axisymmetric elements it is a characteristic length in the r–z plane only. For cohesive elements it is equal to the constitutive thickness. This definition of the characteristic length is used because we do not necessarily know in which direction the concrete will crack; and, hence, we cannot choose the length measure a priori in any particular direction. These characteristic length estimates are appropriate only for well-shaped elements (elements that do not have large aspect ratios), which should be considered by the user in defining values for the material properties. Alternatively, this mesh dependency could be reduced by directly specifying the characteristic length as a function of element topology and material orientation in user subroutine VUCHARLENGTH, as described in VUCHARLENGTH.

For reinforced concrete, since Abaqus provides no direct modeling of the bond between rebar and concrete, the effect of this bond on the concrete cracks must be smeared into the plain concrete part of the model. This effect is generally accomplished by increasing the value of $G_f^I$ based on comparisons with experiments on reinforced material. This increased ductility is commonly refered to as the “tension stiffening” effect.

In reinforced concrete applications the softening behavior of the concrete tends to have less influence on the overall response of the structure because of the stabilizing presence of the rebar. Therefore, it is often appropriate to define tension stiffening as a ${\sigma }_t^I$–$e_{nn}^{ck}$ relationship directly. This option is also offered in Abaqus.

An important feature of the cracking model is that, whereas crack initiation is based on Mode I fracture only, postcracked behavior includes Mode II as well as Mode I. The Mode II shear behavior is described next.

The Mode II model is based on the common observation that the shear behavior is dependent on the amount of crack opening. Therefore, Abaqus offers a shear retention model in which the postcracked shear stiffness is dependent on crack opening. This model defines the total shear stress as a function of the total shear strain (shear direction $nt$ is used as an example):

where $D_{nt}^{II}\left(e_{nn}^{ck},e_{tt}^{ck}\right)$ is a stiffness that depends on crack opening. $D_{nt}^{II}$ can be expressed as

where G is the shear modulus of the uncracked concrete and $\alpha \left(e_{nn}^{ck},e_{tt}^{ck}\right)$ is a user-defined dependence of the form shown in Figure 8.

Figure 8. Shear retention factor dependence on crack opening.

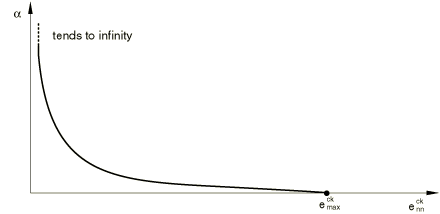
A commonly used mathematical form for this dependence when there is only one crack, associated with direction n, is the power law proposed by Rots and Blaauwendraad (1989):

where p and $e_{max}^{ck}$ are material parameters. This form satisfies the requirements that $\alpha \to \mathrm{\infty }$ as $e_{nn}^{ck}\to 0$ (corresponding to the state before crack initiation) and $\alpha \to 0$ as $e_{nn}^{ck}\to e_{max}^{ck}$ (corresponding to complete loss of aggregate interlock). Note that the bounds of $\alpha$, as defined in our model using the elastic-cracking strain decomposition, are $\mathrm{\infty }$ and zero. This contrasts with some of the traditional shear retention models where the intact concrete and cracking strains are not separated; the shear retention in these models is defined using a shear retention factor, $\rho$, which can have values between one and zero. The relationship between these two shear retention parameters is

The shear retention power law form given in Equation 13 can then be written in terms of $\rho$ as

Since users are more accustomed to specifying shear retention factors in the traditional way (with values between one and zero), the Abaqus input requests $\rho$–$e_{nn}^{ck}$ data. Using Equation 14, these data are then converted to $\alpha$–$e_{nn}^{ck}$ data for computation purposes.

When the shear component under consideration is associated with only one open crack direction (n or t), the crack opening dependence is obtained directly from Figure 8. However, when the shear direction is associated with two open crack directions (n and t), then

with

and, therefore,

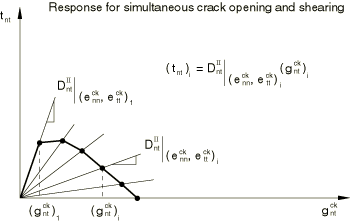
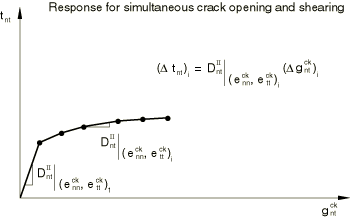
This total stress-strain shear retention model differs from the traditional shear retention models in which the stress-strain relations are written in incremental form (again, shear direction $nt$ is used as an example):

where $D_{nt}^{II}\left(e_{nn}^{ck},e_{tt}^{ck}\right)$ is an incremental stiffness that depends on crack opening. The difference between the total model used in Abaqus (Equation 12) and the traditional incremental model (Equation 15) is best illustrated by considering the shear response of the two models in the case when a crack is simultaneously opening and shearing. This is shown in Figure 9 for the total model and in Figure 10 for the incremental model. It is apparent that, in the total model, the shear stress tends to zero as the crack opens and shears; whereas, in the incremental model the shear stress tends to a finite value. This may explain why overly stiff responses are usually obtained with the traditional shear retention models.

Figure 9. Abaqus crack opening–dependent shear retention (total) model.

Figure 10. Traditional crack opening–dependent shear retention (incremental) model.