Damaged plasticity model for concrete and other quasi-brittle materials

This section describes the concrete damaged plasticity model provided in Abaqus for the analysis of concrete and other quasi-brittle materials.

The following topics are discussed:

About the inviscid concrete damaged plasticity model
Damage and stiffness degradation
Yield condition
Flow rule
Viscoplastic regularization
Integration of the model

ProductsAbaqus/StandardAbaqus/Explicit

The material library in Abaqus also includes other constitutive models for concrete based on the smeared crack approach. These are the smeared crack model in Abaqus/Standard, described in An inelastic constitutive model for concrete, and the brittle cracking model in Abaqus/Explicit, described in A cracking model for concrete and other brittle materials.

The concrete damaged plasticity model is primarily intended to provide a general capability for the analysis of concrete structures under cyclic and/or dynamic loading. The model is also suitable for the analysis of other quasi-brittle materials, such as rock, mortar and ceramics; but it is the behavior of concrete that is used in the remainder of this section to motivate different aspects of the constitutive theory. Under low confining pressures, concrete behaves in a brittle manner; the main failure mechanisms are cracking in tension and crushing in compression. The brittle behavior of concrete disappears when the confining pressure is sufficiently large to prevent crack propagation. In these circumstances failure is driven by the consolidation and collapse of the concrete microporous microstructure, leading to a macroscopic response that resembles that of a ductile material with work hardening.

Modeling the behavior of concrete under large hydrostatic pressures is out of the scope of the plastic-damage model considered here. The constitutive theory in this section aims to capture the effects of irreversible damage associated with the failure mechanisms that occur in concrete and other quasi-brittle materials under fairly low confining pressures (less than four or five times the ultimate compressive stress in uniaxial compression loading). These effects manifest themselves in the following macroscopic properties:

different yield strengths in tension and compression, with the initial yield stress in compression being a factor of 10 or more higher than the initial yield stress in tension;
softening behavior in tension as opposed to initial hardening followed by softening in compression;
different degradation of the elastic stiffness in tension and compression;
stiffness recovery effects during cyclic loading; and
rate sensitivity, especially an increase in the peak strength with strain rate.

The plastic-damage model in Abaqus is based on the models proposed by Lubliner et al. (1989) and by Lee and Fenves (1998). The model is described in the remainder of this section. An overview of the main ingredients of the model is given first, followed by a more detailed discussion of the different aspects of the constitutive model.

About the inviscid concrete damaged plasticity model

The main ingredients of the inviscid concrete damaged plasticity model are summarized below.

Strain rate decomposition

An additive strain rate decomposition is assumed for the rate-independent model:

\dot{ε} = {\dot{ε}}^{e l} + {\dot{ε}}^{p l},

where $\dot{ε}$ is the total strain rate, ${\dot{ε}}^{e l}$ is the elastic part of the strain rate, and ${\dot{ε}}^{p l}$ is the plastic part of the strain rate.

Stress-strain relations

The stress-strain relations are governed by scalar damaged elasticity:

σ = (1 - d) D_{0}^{e l} : (ε - ε^{p l}) = D^{e l} : (ε - ε^{p l}),

where $D_{0}^{e l}$ is the initial (undamaged) elastic stiffness of the material; $D^{e l} = (1 - d) D_{0}^{e l}$ is the degraded elastic stiffness; and d is the scalar stiffness degradation variable, which can take values in the range from zero (undamaged material) to one (fully damaged material). Damage associated with the failure mechanisms of the concrete (cracking and crushing) therefore results in a reduction in the elastic stiffness. Within the context of the scalar-damage theory, the stiffness degradation is isotropic and characterized by a single degradation variable, d. Following the usual notions of continuum damage mechanics, the effective stress is defined as

\bar{σ} \overset{def}{=} D_{0}^{e l} : (ε - ε^{p l}) .

The Cauchy stress is related to the effective stress through the scalar degradation relation:

σ = (1 - d) \bar{σ} .

For any given cross-section of the material, the factor $(1 - d)$ represents the ratio of the effective load-carrying area (i.e., the overall area minus the damaged area) to the overall section area. In the absence of damage, $d = 0$ , the effective stress $\bar{σ}$ is equivalent to the Cauchy stress, $σ$ . When damage occurs, however, the effective stress is more representative than the Cauchy stress because it is the effective stress area that is resisting the external loads. It is, therefore, convenient to formulate the plasticity problem in terms of the effective stress. As discussed later, the evolution of the degradation variable is governed by a set of hardening variables, ${\tilde{ε}}^{p l}$ , and the effective stress; that is, $d = d (\bar{σ}, {\tilde{ε}}^{p l})$ .

Hardening variables

Damaged states in tension and compression are characterized independently by two hardening variables, ${\tilde{ε}}_{t}^{p l}$ and ${\tilde{ε}}_{c}^{p l}$ , which are referred to as equivalent plastic strains in tension and compression, respectively. The evolution of the hardening variables is given by an expression of the form

{\tilde{ε}}^{p l} = [\begin{matrix} {\tilde{ε}}_{t}^{p l} \\ {\tilde{ε}}_{c}^{p l} \end{matrix}]; {\dot{\tilde{ε}}}^{p l} = h (\bar{σ}, {\tilde{ε}}^{p l}) \cdot {\dot{ε}}^{p l},

as described later in this section.

Microcracking and crushing in the concrete are represented by increasing values of the hardening variables. These variables control the evolution of the yield surface and the degradation of the elastic stiffness. They are also intimately related to the dissipated fracture energy required to generate micro-cracks.

Yield function

The yield function, $F (\bar{σ}, {\tilde{ε}}^{p l})$ , represents a surface in effective stress space, which determines the states of failure or damage. For the inviscid plastic-damage model

F (\bar{σ}, {\tilde{ε}}^{p l}) \leq 0.

The specific form of the yield function is described later in this section.

Flow rule

Plastic flow is governed by a flow potential G according to the flow rule:

{\dot{ε}}^{p l} = \dot{λ} \frac{\partial G (\bar{σ})}{\partial \bar{σ}},

where $\dot{λ}$ is the nonnegative plastic multiplier. The plastic potential is defined in the effective stress space. The specific form of the flow potential for the concrete damaged plasticity model is discussed later in this section. The model uses nonassociated plasticity, therefore requiring the solution of nonsymmetric equations.

Summary

In summary, the elastic-plastic response of the concrete damaged plasticity model is described in terms of the effective stress and the hardening variables:

\begin{matrix} (1) & \begin{matrix} \bar{σ} = D_{0}^{e l} : (ε - ε^{p l}) \in {\bar{σ} | F (\bar{σ}, {\tilde{ε}}^{p l}) \leq 0}, \\ {\dot{\tilde{ε}}}^{p l} = h (\bar{σ}, {\tilde{ε}}^{p l}) \cdot {\dot{ε}}^{p l}, \\ {\dot{ε}}^{p l} = \dot{λ} \frac{\partial G (\bar{σ})}{\partial \bar{σ}}, \end{matrix} \end{matrix}

where $\dot{λ}$ and F obey the Kuhn-Tucker conditions: $\dot{λ} F = 0; \dot{λ} \geq 0; F \leq 0$ The Cauchy stress is calculated in terms of the stiffness degradation variable, $d (\bar{σ}, {\tilde{ε}}^{p l})$ , and the effective stress as

\begin{matrix} (2) & σ = (1 - d) \bar{σ} . \end{matrix}

The constitutive relations for the elastic-plastic response, Equation 1, are decoupled from the stiffness degradation response, Equation 2, which makes the model attractive for an effective numerical implementation. The inviscid model summarized here can be extended easily to account for viscoplastic effects through the use of a viscoplastic regularization by permitting stresses to be outside the yield surface.

Damage and stiffness degradation

The evolution equations of the hardening variables ${\tilde{ε}}_{t}^{p l}$ and ${\tilde{ε}}_{c}^{p l}$ are conveniently formulated by considering uniaxial loading conditions first and then extended to multiaxial conditions.

Uniaxial conditions

It is assumed that the uniaxial stress-strain curves can be converted into stress versus plastic strain curves of the form

\begin{matrix} (3) & \begin{matrix} σ_{t} & = σ_{t} ({\tilde{ε}}_{t}^{p l}, {\dot{\tilde{ε}}}_{t}^{p l}, θ, f_{i}), \\ σ_{c} & = σ_{c} ({\tilde{ε}}_{c}^{p l}, {\dot{\tilde{ε}}}_{c}^{p l}, θ, f_{i}), \end{matrix} \end{matrix}

where the subscripts t and c refer to tension and compression, respectively; ${\dot{\tilde{ε}}}_{t}^{p l}$ and ${\dot{\tilde{ε}}}_{c}^{p l}$ are the equivalent plastic strain rates, ${\tilde{ε}}_{t}^{p l} = \int_{0}^{t} {\dot{\tilde{ε}}}_{t}^{p l} d t$ and ${\tilde{ε}}_{c}^{p l} = \int_{0}^{t} {\dot{\tilde{ε}}}_{c}^{p l} d t$ are the equivalent plastic strains, $θ$ is the temperature, and $f_{i}, (i = 1, 2, \dots)$ are other predefined field variables.

Under uniaxial loading conditions the effective plastic strain rates are given as

\begin{matrix} (4) & \begin{matrix} {\dot{\tilde{ε}}}_{t}^{p l} & = {\dot{ε}}_{11}^{p l}, in
  uniaxial tension
  and \\ {\dot{\tilde{ε}}}_{c}^{p l} & = - {\dot{ε}}_{11}^{p l}, in
  uniaxial
  compression. \end{matrix} \end{matrix}

In the remainder of this section we adopt the convention that $σ_{c}$ is a positive quantity representing the magnitude of the uniaxial compression stress; that is, $σ_{c} = - σ_{11}$ .

As shown in Figure 1, when the concrete specimen is unloaded from any point on the strain softening branch of the stress-strain curves, the unloading response is observed to be weakened: the elastic stiffness of the material appears to be damaged (or degraded). The degradation of the elastic stiffness is significantly different between tension and compression tests; in either case, the effect is more pronounced as the plastic strain increases. The degraded response of concrete is characterized by two independent uniaxial damage variables, $d_{t}$ and $d_{c}$ , which are assumed to be functions of the plastic strains, temperature, and field variables:

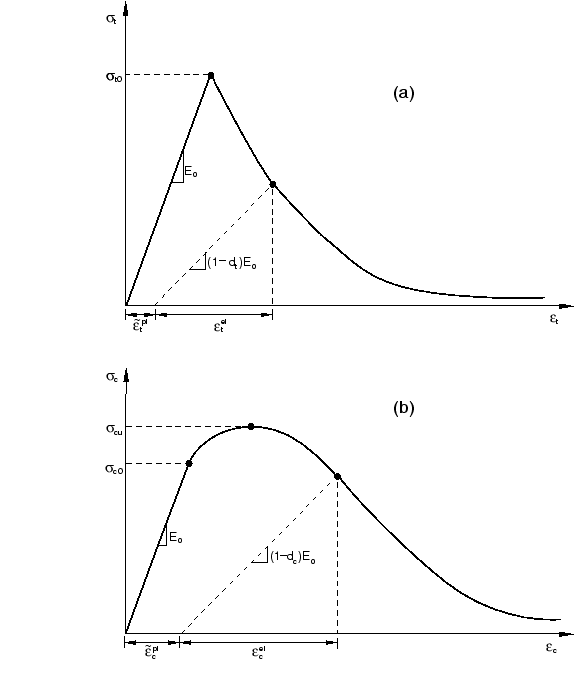
\begin{matrix} (5) & \begin{matrix} d_{t} & = d_{t} ({\tilde{ε}}_{t}^{p l}, θ, f_{i}), (0 \leq d_{t} \leq 1), \\ d_{c} & = d_{c} ({\tilde{ε}}_{c}^{p l}, θ, f_{i}), (0 \leq d_{c} \leq 1) . \end{matrix} \end{matrix}

Figure 1. Response of concrete to uniaxial loading in tension (a) and compression (b).

The uniaxial degradation variables are increasing functions of the equivalent plastic strains. They can take values ranging from zero, for the undamaged material, to one, for the fully damaged material.

If $E_{0}$ is the initial (undamaged) elastic stiffness of the material, the stress-strain relations under uniaxial tension and compression loading are, respectively:

\begin{matrix} σ_{t} & = (1 - d_{t}) E_{0} (ε_{t} - {\tilde{ε}}_{t}^{p l}), \\ σ_{c} & = (1 - d_{c}) E_{0} (ε_{c} - {\tilde{ε}}_{c}^{p l}) . \end{matrix}

Under uniaxial loading cracks propagate in a direction transverse to the stress direction. The nucleation and propagation of cracks, therefore, causes a reduction of the available load-carrying area, which in turn leads to an increase in the effective stress. The effect is less pronounced under compressive loading since cracks run parallel to the loading direction; however, after a significant amount of crushing, the effective load-carrying area is also significantly reduced. The effective uniaxial cohesion stresses, ${\bar{σ}}_{t}$ and ${\bar{σ}}_{c}$ , are given as

\begin{matrix} {\bar{σ}}_{t} & = \frac{σ_{t}}{(1 - d_{t})} = E_{0} (ε_{t} - {\tilde{ε}}_{t}^{p l}), \\ {\bar{σ}}_{c} & = \frac{σ_{c}}{(1 - d_{c})} = E_{0} (ε_{c} - {\tilde{ε}}_{c}^{p l}) . \end{matrix}

The effective uniaxial cohesion stresses determine the size of the yield (or failure) surface.

Uniaxial cyclic conditions

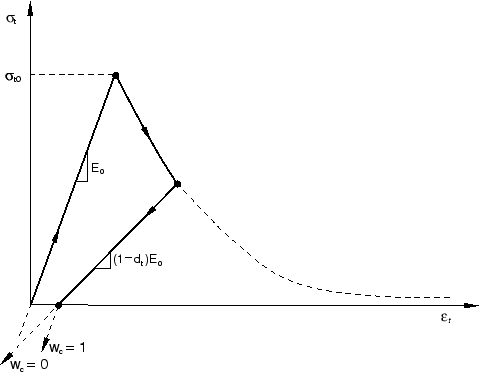
Under uniaxial cyclic loading conditions the degradation mechanisms are quite complex, involving the opening and closing of previously formed micro-cracks, as well as their interaction. Experimentally, it is observed that there is some recovery of the elastic stiffness as the load changes sign during a uniaxial cyclic test. The stiffness recovery effect, also known as the “unilateral effect,” is an important aspect of the concrete behavior under cyclic loading. The effect is usually more pronounced as the load changes from tension to compression, causing tensile cracks to close, which results in the recovery of the compressive stiffness.

The concrete damaged plasticity model assumes that the reduction of the elastic modulus is given in terms of a scalar degradation variable, d, as

E = (1 - d) E_{0},

where $E_{0}$ is the initial (undamaged) modulus of the material.

This expression holds both in the tensile ( $σ_{11} > 0$ ) and compressive ( $σ_{11} < 0$ ) sides of the cycle. The stiffness reduction variable, d, is a function of the stress state and the uniaxial damage variables, $d_{t}$ and $d_{c}$ . For the uniaxial cyclic conditions, Abaqus assumes that

\begin{matrix} (6) & (1 - d) = (1 - s_{t} d_{c}) (1 - s_{c} d_{t}), 0 \leq s_{t}, s_{c} \leq 1, \end{matrix}

where $s_{t}$ and $s_{c}$ are functions of the stress state that are introduced to represent stiffness recovery effects associated with stress reversals. They are defined according to

\begin{matrix} s_{t} & = 1 - w_{t} r^{*} ({\bar{σ}}_{11}); 0 \leq w_{t} \leq 1, \\ s_{c} & = 1 - w_{c} (1 - r^{*} ({\bar{σ}}_{11})); 0 \leq w_{c} \leq 1, \end{matrix}

where

r^{*} ({\bar{σ}}_{11}) = H ({\bar{σ}}_{11}) = {\begin{matrix} 1 & if & {\bar{σ}}_{11} > 0 \\ 0 & if & {\bar{σ}}_{11} < 0 \end{matrix} .

The weight factors $w_{t}$ and $w_{c}$ , which are assumed to be material properties, control the recovery of the tensile and compressive stiffness upon load reversal. To illustrate this, consider the example in Figure 2, where the load changes from tension to compression. Assume that there was no previous compressive damage (crushing) in the material; that is, ${\tilde{ε}}_{c}^{p l} = 0$ and $d_{c} = 0$ . Then

(1 - d) = (1 - s_{c} d_{t}) = (1 - (1 - w_{c} (1 - r^{*})) d_{t}) .

In tension ( ${\bar{σ}}_{11} > 0$ ), $r^{*} = 1$ ; thus, $d = d_{t}$ as expected. In compression ( ${\bar{σ}}_{11} < 0$ ), $r^{*} = 0$ , and $d = (1 - w_{c}) d_{t}$ . If $w_{c} = 1$ , then $d = 0$ ; therefore, the material fully recovers the compressive stiffness (which in this case is the initial undamaged stiffness, $E = E_{0}$ ). If, on the other hand, $w_{c} = 0$ , then $d = d_{t}$ and there is no stiffness recovery. Intermediate values of $w_{c}$ result in partial recovery of the stiffness.

Figure 2. Illustration of the effect of the compression stiffness recovery parameter

w_{c}

The evolution equations of the equivalent plastic strains are also generalized to the uniaxial cyclic conditions as

\begin{matrix} (7) & \begin{matrix} {\dot{\tilde{ε}}}_{t}^{p l} & = r^{*} {\dot{ε}}_{11}^{p l}, \\ {\dot{\tilde{ε}}}_{c}^{p l} & = - (1 - r^{*}) {\dot{ε}}_{11}^{p l}, \end{matrix} \end{matrix}

which clearly reduces to Equation 4 during the tensile and compressive phases of the cycle.

Multiaxial conditions

The evolution equations for the hardening variables must be extended for the general multiaxial conditions. Based on Lee and Fenves (1998) we assume that the equivalent plastic strain rates are evaluated according to the expressions

\begin{matrix} (8) & \begin{matrix} {\dot{\tilde{ε}}}_{t}^{p l} & \overset{def}{=} r (\hat{\bar{σ}}) {\hat{\dot{ε}}}_{\max}^{p l}, \\ {\dot{\tilde{ε}}}_{c}^{p l} & \overset{def}{=} - (1 - r (\hat{\bar{σ}})) {\hat{\dot{ε}}}_{\min}^{p l}, \end{matrix} \end{matrix}

where ${\hat{\dot{ε}}}_{\max}^{p l}$ and ${\hat{\dot{ε}}}_{\min}^{p l}$ are, respectively, the maximum and minimum eigenvalues of the plastic strain rate tensor ${\dot{ε}}^{p l}$ and

r (\hat{\bar{σ}}) \overset{def}{=} \frac{\overset{3}{\sum_{i = 1}} ⟨ {\hat{\bar{σ}}}_{i} ⟩}{\sum_{i = 1}^{3} | {\hat{\bar{σ}}}_{i} |}; 0 \leq r (\hat{\bar{σ}}) \leq 1

is a stress weight factor that is equal to one if all principal stresses ${\hat{\bar{σ}}}_{i}, (i = 1, 2, 3)$ , are positive and equal to zero if they are negative. The Macauley bracket $⟨ \cdot ⟩$ is defined by $⟨ x ⟩ = \frac{1}{2} (| x | + x)$ . In uniaxial loading conditions Equation 8 reduces to the uniaxial definitions Equation 4 and Equation 7, since ${\hat{\dot{ε}}}_{\max}^{p l} = {\dot{ε}}_{11}^{p l}$ in tension, and ${\hat{\dot{ε}}}_{\min}^{p l} = {\dot{ε}}_{11}^{p l}$ in compression.

If the eigenvalues of the plastic strain rate tensor ( ${\hat{\dot{ε}}}_{i}, i = 1, 2, 3$ ) are ordered such that ${\hat{\dot{ε}}}_{\max}^{p l} = {\hat{\dot{ε}}}_{1} \geq {\hat{\dot{ε}}}_{2} \geq {\hat{\dot{ε}}}_{3} = {\hat{\dot{ε}}}_{\min}^{p l}$ , the evolution equation for general multiaxial stress conditions can be expressed in the following matrix form:

{\dot{\tilde{ε}}}^{p l} = [\begin{matrix} {\dot{\tilde{ε}}}_{t}^{p l} \\ {\dot{\tilde{ε}}}_{c}^{p l} \end{matrix}] = \hat{h} (\hat{\bar{σ}}, {\tilde{ε}}^{p l}) \cdot {\hat{\dot{ε}}}^{p l},

where

\hat{h} (\hat{\bar{σ}}, {\tilde{ε}}^{p l}) = [\begin{matrix} r (\hat{\bar{σ}}) & 0 & 0 \\ 0 & 0 & - (1 - r (\hat{\bar{σ}})) \end{matrix}],

and

{\hat{\dot{ε}}}^{p l} = [\begin{matrix} {\hat{\dot{ε}}}_{1} \\ {\hat{\dot{ε}}}_{2} \\ {\hat{\dot{ε}}}_{3} \end{matrix}] .

Elastic stiffness degradation

The plastic-damage concrete model assumes that the elastic stiffness degradation is isotropic and characterized by a single scalar variable, d:

\begin{matrix} (9) & D^{e l} = (1 - d) D_{0}^{e l}; 0 \leq d \leq 1. \end{matrix}

The definition of the scalar degradation variable d must be consistent with the uniaxial monotonic responses ( $d_{t}$ and $d_{c}$ ), and it should also should capture the complexity associated with the degradation mechanisms under cyclic loading. For the general multiaxial stress conditions Abaqus assumes that

\begin{matrix} (10) & (1 - d) = (1 - s_{t} d_{c}) (1 - s_{c} d_{t}), 0 \leq s_{t}, s_{c} \leq 1, \end{matrix}

similar to the uniaxial cyclic case, only that $s_{t}$ and $s_{c}$ are now given in terms of the function $r (\hat{\bar{σ}})$ as

\begin{matrix} s_{t} & = 1 - w_{t} r (\hat{\bar{σ}}); 0 \leq w_{t} \leq 1, \\ s_{c} & = 1 - w_{c} (1 - r (\hat{\bar{σ}})); 0 \leq w_{c} \leq 1. \end{matrix}

It can be easily verified that Equation 10 for the scalar degradation variable is consistent with the uniaxial response.

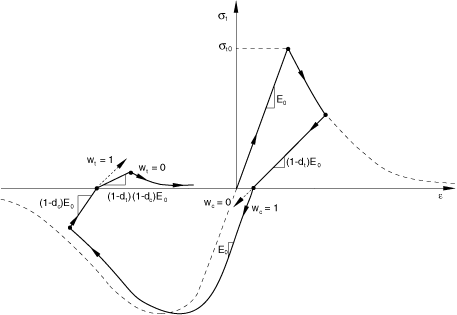
The experimental observation in most quasi-brittle materials, including concrete, is that the compressive stiffness is recovered upon crack closure as the load changes from tension to compression. On the other hand, the tensile stiffness is not recovered as the load changes from compression to tension once crushing micro-cracks have developed. This behavior, which corresponds to $w_{t} = 0$ and $w_{c} = 1$ , is the default used by Abaqus. Figure 3 illustrates a uniaxial load cycle assuming the default behavior.

Figure 3. Uniaxial load cycle (tension-compression-tension) assuming default values for the stiffness recovery factors:

w_{t} = 0

and

w_{c} = 1

Yield condition

The plastic-damage concrete model uses a yield condition based on the yield function proposed by Lubliner et al. (1989) and incorporates the modifications proposed by Lee and Fenves (1998) to account for different evolution of strength under tension and compression. In terms of effective stresses the yield function takes the form

\begin{matrix} (11) & F (\bar{σ}, {\tilde{ε}}^{p l}) = \frac{1}{1 - α} (\bar{q} - 3 α \bar{p} + β ({\tilde{ε}}^{p l}) ⟨ {\hat{\bar{σ}}}_{\max} ⟩ - γ ⟨ - {\hat{\bar{σ}}}_{\max} ⟩) - {\bar{σ}}_{c} ({\tilde{ε}}_{c}^{p l}) \leq 0, \end{matrix}

where $α$ and $γ$ are dimensionless material constants;

\bar{p} = - \frac{1}{3} \bar{σ} : I

is the effective hydrostatic pressure;

\bar{q} = \sqrt{\frac{3}{2} \bar{S} : \bar{S}}

is the Mises equivalent effective stress;

\bar{S} = \bar{p} I + \bar{σ},

is the deviatoric part of the effective stress tensor $\bar{σ}$ ; and ${\hat{\bar{σ}}}_{\max}$ is the algebraically maximum eigenvalue of $\bar{σ}$ . The function $β ({\tilde{ε}}^{p l})$ is given as

β ({\tilde{ε}}^{p l}) = \frac{{\bar{σ}}_{c} ({\tilde{ε}}_{c}^{p l})}{{\bar{σ}}_{t} ({\tilde{ε}}_{t}^{p l})} (1 - α) - (1 + α),

where ${\bar{σ}}_{t}$ and ${\bar{σ}}_{c}$ are the effective tensile and compressive cohesion stresses, respectively.

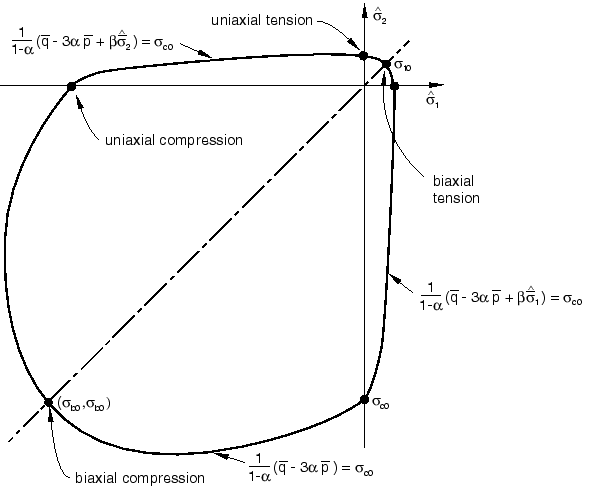
In biaxial compression, with ${\hat{\bar{σ}}}_{\max} = 0$ , Equation 11 reduces to the well-known Drucker-Prager yield condition. The coefficient $α$ can be determined from the initial equibiaxial and uniaxial compressive yield stress, $σ_{b 0}$ and $σ_{c 0}$ , as

α = \frac{σ_{b 0} - σ_{c 0}}{2 σ_{b 0} - σ_{c 0}} .

Typical experimental values of the ratio $σ_{b 0} / σ_{c 0}$ for concrete are in the range from 1.10 to 1.16, yielding values of $α$ between 0.08 and 0.12 (Lubliner et al., 1989).

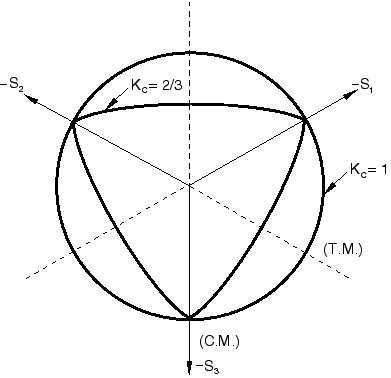
The coefficient $γ$ enters the yield function only for stress states of triaxial compression, when ${\hat{\bar{σ}}}_{\max} < 0.$ This coefficient can be determined by comparing the yield conditions along the tensile and compressive meridians. By definition, the tensile meridian (TM) is the locus of stress states satisfying the condition ${\hat{\bar{σ}}}_{\max} = {\hat{\bar{σ}}}_{1} > {\hat{\bar{σ}}}_{2} = {\hat{\bar{σ}}}_{3}$ and the compressive meridian (CM) is the locus of stress states such that ${\hat{\bar{σ}}}_{\max} = {\hat{\bar{σ}}}_{1} = {\hat{\bar{σ}}}_{2} > {\hat{\bar{σ}}}_{3}$ , where ${\hat{\bar{σ}}}_{1}$ , ${\hat{\bar{σ}}}_{2}$ , and ${\hat{\bar{σ}}}_{3}$ are the eigenvalues of the effective stress tensor. It can be easily shown that ${({\hat{\bar{σ}}}_{\max})}_{TM} = \frac{2}{3} \bar{q} - \bar{p}$ and ${({\hat{\bar{σ}}}_{\max})}_{CM} = \frac{1}{3} \bar{q} - \bar{p}$ , along the tensile and compressive meridians, respectively. With ${\hat{\bar{σ}}}_{\max} < 0$ the corresponding yield conditions are

(\frac{2}{3} γ + 1) \bar{q} - (γ + 3 α) \bar{p} = (1 - α) {\bar{σ}}_{c}, (TM)

(\frac{1}{3} γ + 1) \bar{q} - (γ + 3 α) \bar{p} = (1 - α) {\bar{σ}}_{c} . (CM)

Let $K_{c} = {\bar{q}}_{(TM)} / {\bar{q}}_{(CM)}$ for any given value of the hydrostatic pressure $\bar{p}$ with ${\hat{\bar{σ}}}_{\max} < 0$ ; then

K_{c} = \frac{γ + 3}{2 γ + 3} .

The fact that $K_{c}$ is constant does not seem to be contradicted by experimental evidence (Lubliner et al., 1989). The coefficient $γ$ is, therefore, evaluated as

γ = \frac{3 (1 - K_{c})}{2 K_{c} - 1} .

A value of $K_{c} = \frac{2}{3}$ , which is typical for concrete, gives $γ = 3$

If ${\hat{\bar{σ}}}_{\max} > 0$ , the yield conditions along the tensile and compressive meridians reduce to

(\frac{2}{3} β + 1) \bar{q} - (β + 3 α) \bar{p} = (1 - α) \bar{σ_{c}}, (TM)

(\frac{1}{3} β + 1) \bar{q} - (β + 3 α) \bar{p} = (1 - α) {\bar{σ}}_{c} . (CM)

Let $K_{t} = {\bar{q}}_{(TM)} / {\bar{q}}_{(CM)}$ for any given value of the hydrostatic pressure $\bar{p}$ with ${\hat{\bar{σ}}}_{\max} > 0$ ; then

K_{t} = \frac{β + 3}{2 β + 3} .

Typical yield surfaces are shown in Figure 4 in the deviatoric plane and in Figure 5 for plane-stress conditions.

Figure 4. Yield surfaces in the deviatoric plane, corresponding to different values of

K_{c}

Figure 5. Yield surface in plane stress.

Flow rule

The plastic-damage model assumes nonassociated potential flow,

{\dot{ε}}^{p l} = \dot{λ} \frac{\partial G (\bar{σ})}{\partial \bar{σ}} .

The flow potential G chosen for this model is the Drucker-Prager hyperbolic function:

\begin{matrix} (12) & G = \sqrt{{(ϵ σ_{t 0} \tan ψ)}^{2} + {\bar{q}}^{2}} - \bar{p} \tan ψ, \end{matrix}

where $ψ$ is the dilation angle measured in the p–q plane at high confining pressure; $σ_{t 0}$ is the uniaxial tensile stress at failure; and $ϵ$ is a parameter, referred to as the eccentricity, that defines the rate at which the function approaches the asymptote (the flow potential tends to a straight line as the eccentricity tends to zero). This flow potential, which is continuous and smooth, ensures that the flow direction is defined uniquely. The function asymptotically approaches the linear Drucker-Prager flow potential at high confining pressure stress and intersects the hydrostatic pressure axis at 90°. See Models for granular or polymer behavior for further discussion of this potential.

Because plastic flow is nonassociated, the use of the plastic-damage concrete model requires the solution of nonsymmetric equations.

Viscoplastic regularization

Material models exhibiting softening behavior and stiffness degradation often lead to severe convergence difficulties in implicit analysis programs. Some of these convergence difficulties can be overcome by using a viscoplastic regularization of the constitutive equations. The concrete damaged plasticity model can be regularized using viscoplasticity, therefore permitting stresses to be outside of the yield surface. We use a generalization of the Duvaut-Lions regularization, according to which the viscoplastic strain rate tensor, ${\dot{ε}}_{v}^{p l}$ , is defined as

\begin{matrix} (13) & {\dot{ε}}_{v}^{p l} = \frac{1}{μ} (ε^{p l} - ε_{v}^{p l}) . \end{matrix}

Here $μ$ is the viscosity parameter representing the relaxation time of the viscoplastic system and $ε^{p l}$ is the plastic strain evaluated in the inviscid backbone model.

Similarly, a viscous stiffness degradation variable, $d_{v}$ , for the viscoplastic system is defined as

\begin{matrix} (14) & {\dot{d}}_{v} = \frac{1}{μ} (d - d_{v}), \end{matrix}

where d is the degradation variable evaluated in the inviscid backbone model. The stress-strain relation of the viscoplastic model is given as

\begin{matrix} (15) & σ = (1 - d_{v}) D_{0}^{e l} : (ε - ε_{v}^{p l}) . \end{matrix}

The solution of the viscoplastic system relaxes to that of the inviscid case as $t / μ \to \infty$ , where t represents time. Using the viscoplastic regularization with a small value for the viscosity parameter (small compared to the characteristic time increment) usually helps improve the rate of convergence of the model in the softening regime, without compromising results.

Integration of the model

The model is integrated using the backward Euler method generally used with the plasticity models in Abaqus. A material Jacobian consistent with this integration operator is used for the equilibrium iterations.