Mean-field homogenization

Mean-field homogenization:

is a semi-analytical homogenization approach that can be used to compute thermal and mechanical properties of a composite material;
can also predict volume-averaged micro-level solutions in each constituent of the composite; and
uses formulations based on Eshelby's solution.

The following topics are discussed:

Mean-field homogenization for linear elastic composites
Incremental mean-field homogenization for nonlinear composites
Multi-step homogenization
Specifying the microstructure of the composite
Composites with thermal expansion
Example
Elements
Output
References

Mean-field homogenization for linear elastic composites

The mean-field strain and stress in each phase I is defined as

{\bar{σ}}_{I} = {〈 σ 〉}_{I}

{\bar{ϵ}}_{I} = {〈 ϵ 〉}_{I},

where

〈 f 〉 = \frac{1}{V} \int_{V}^{} f d V .

The averaged macro fields can be written as

〈 • 〉 = v_{f}^{M} {〈 • 〉}_{M} + \sum_{I = 1}^{N} v_{f}^{I} {〈 • 〉}_{I},

where $v_{f}^{M}$ is the volume fraction of the matrix phase and $v_{f}^{I}$ is the volume fraction of the inclusion phase. For the single-inclusion case, if all the constituents are linear elastic, the strain in the inclusion is related to the strain in the matrix through a concentration tensor $A$ .

{〈 ϵ 〉}_{I} = A {〈 ϵ 〉}_{M} .

The form of the concentration tensor defines the homogenization methods below.

Voigt and Reuss models

The simplest mean-field homogenization formulations are the Voigt and Reuss models. These models do not take into account the shape or the orientation of the inclusions; however, they provide upper and lower bounds of the macro stiffness modulus and, therefore, can be used for validation. The Voigt model is also used in a two-step approach to model composites with multiple inclusions.

The Voigt model assumes uniform strain in the composite ${〈 ϵ 〉}_{I} = {〈 ϵ 〉}_{M}$ , which gives

A = I .

The Reuss model assumes uniform stress in the composite ${〈 σ 〉}_{I} = {〈 σ 〉}_{M}$ , which gives

A = C_{I}^{- 1} C_{M},

where $C_{M}$ is the stiffness of the matrix and $C_{I}$ is the stiffness of the inclusion.

Input File Usage

Use the following option to specify the Voigt model as the homogenization method:

 MEAN FIELD HOMOGENIZATION, FORMULATION=VOIGT

Use the following option to specify the Reuss model as the homogenization method:

 MEAN FIELD HOMOGENIZATION, FORMULATION=REUSS

Eshelby-based models

The more sophisticated mean-field homogenizations are based on Eshelby's solution. In his 1957 paper (Eshelby, 1957), Eshelby solved a single-inclusion problem described in Figure 1.

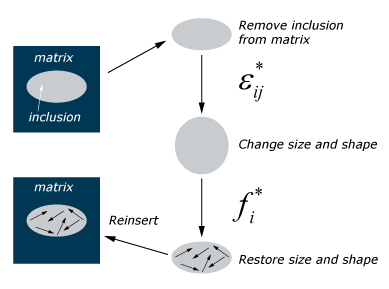
Figure 1. Eshelby's problem: an ellipsoid is cut out of an infinite matrix, undergoes an eigenstrain, and is inserted back into the matrix.

Eshelby found that the strain inside the constrained ellipsoid is uniform and given by

ϵ (x) = E : ϵ^{*},

where $x$ represents a point inside the inclusion and $ϵ^{*}$ is the eigenstrain. The Eshelby tensor (E) is a function of the stiffness of the matrix and also the shape and orientation of the inclusion. To calculate Eshelby's tensor usually involves numerical integration over the surface of the ellipsoidal inclusion; however, analytical solutions are available (Mura, 1987) for simple shapes such as a sphere, cylinder, penny, oblate, and prolate. Based on Eshelby's solution, the following models are proposed based on different assumptions about the properties of the outer material surrounding the inclusions.

Mori-Tanaka model

The Mori-Tanaka formulation assumes that each inclusion behaves like an isolated inclusion and the strain in the matrix is considered as the far-field strain. Therefore, the concentration tensor can be written as

A = {[E : (C_{M}^{- 1} C_{I} - I) + I]}^{- 1} .

Input File Usage

 MEAN FIELD HOMOGENIZATION, FORMULATION=MT

Inversed Mori-Tanaka model

The inverse Mori-Tanaka formulation assumes a high volume fraction of the inclusion and permutes the properties of the matrix and inclusion in a single inclusion problem, which gives

A = {[E : (C_{I}^{- 1} C_{M} - I) + I]}^{- 1} .

Input File Usage

 MEAN FIELD HOMOGENIZATION, FORMULATION=INVERSED MT

Balanced model

The Mori-Tanaka and inversed Mori-Tanaka formulations give the upper and lower bounds of the composite stiffness for low and high volume fractions. The balanced formulation is the interpolative formulation, which can be written as

H_{1} = {[E : (C_{M}^{- 1} C_{I} - I) + I]}^{- 1},

H_{2} = {[E : (C_{I}^{- 1} C_{M} - I) + I]}^{- 1},

A = {[(1 - φ) H_{1}^{- 1} + φ H_{2}^{- 1}]}^{- 1},

where $φ$ is the smooth interpolation function proposed by Lielens (11)

φ = \frac{1}{2} v_{f}^{I} (1 + v_{f}^{I}) .

Input File Usage

MEAN FIELD HOMOGENIZATION, FORMULATION=BALANCED

Incremental mean-field homogenization for nonlinear composites

An incremental linearization approach is used to extend the homogenization models to composites with nonlinear behavior. The tangent stiffness matrix is used in place of the linear elastic modulus to compute the concentration tensor $A$

▵ ϵ_{I} = A ▵ ϵ_{M} .

Since the tangent matrix is not constant in the nonlinear case and is usually a function of the strain, iterations are performed to guarantee a converged solution of the strain increment in each constituent.

Isotropization methods

Analytical expression of Eshelby's tensor is available only if the inclusions are ellipsoidal and the matrix material is isotropic or transversely isotropic. For matrix materials that are anisotropic, using the stiffness directly to compute the Eshelby's tensor can result in stiffer prediction for the composite behavior (Doghri, 2003). The isotropic part of the tangent stiffness matrix can generally be written as

C^{i s o} = 3 K I^{v o l} + 2 G I^{d e v},

where $K$ is the bulk modulus and $G$ is the shear modulus. $I^{v o l}$ and $I^{d e v}$ are the volumetric and deviatoric part of the fourth-order identity tensor. The method used to extract the isotropic part of the stiffness matrix is not unique, and the accuracy of the prediction varies depending on the properties of the matrix material.

General method

The general method is the most common isotropization method, and it extracts the isotropic part using

K = \frac{1}{3} I^{v o l} : : C^{a n i},

G = \frac{1}{10} I^{d e v} : : C^{a n i} .

The general method can be used for any anisotropic tangent matrix. This method is the default isotropization method.

Input File Usage

CONSTITUENT

Spectral method

The spectral isotropization method can be used if isotropic hardening is defined in the matrix material (Doghri, 2003). The isotropic part of the tangent matrix is given by

K = K_{e},

G = G_{e} (1 - \frac{3 G_{e}}{3 G_{e} + \frac{d σ^{0}}{d {\bar{ϵ}}^{p l}} ({\bar{ϵ}}^{p l})}),

where $K_{e}$ is the elastic bulk modulus, $G_{e}$ is the elastic shear modulus, $σ^{0} ({\bar{ϵ}}^{p l})$ is the yield stress, and ${\bar{ϵ}}^{p l}$ is the equivalent plastic strain.

Input File Usage

CONSTITUENT, ISOTROPIZATION COEFFICIENT=1.0

Modified spectral method

For matrix materials with significant softening after yielding, both the general method and the spectral method might give predictions that are too stiff. The modified spectral method proposed by Selmi et. al. (Selmi, 2011) improves the accuracy of the spectral method by evaluating the derivative of the yield stress at a larger equivalent plastic strain

K = K_{e},

G = G_{e} (1 - \frac{3 G_{e}}{3 G_{e} + \frac{d σ^{0}}{d {\bar{ϵ}}^{p l}} (ξ {\bar{ϵ}}^{p l})}),

where $ξ$ is the isotropization coefficient that can be calibrated by comparing the mean-field solution to experimental data or FE-RVE solutions. The isotropization coefficient is irrelevant if the constituent does not have plastic behavior.

Input File Usage

CONSTITUENT, ISOTROPIZATION COEFFICIENT=isotropization coefficient

Isotropic projection

Options are available to use the isotropic projection of the tangent matrix to compute different parts of the concentration tensor. For better predictions, Doghri et. al (Doghri, 2010) recommended the following:

If the general method is used, only Eshelby's tensor is computed with the isotropic projection.
If the spectral/modified spectral method is used, Hill's tensor given by $P = E : C_{M}^{- 1}$ is computed with the isotropic projection.

It is possible that some choices can lead to unphysical prediction of micro-level strain resulting in unstable material behavior in the composite. In addition, the tangent stiffness matrix for the composite might lose its symmetry after homogenization; therefore, you must use the unsymmetric solver to achieve convergence.

Input File Usage

Use the following option to use the isotropic projection of the matrix stiffness to compute all parts of the concentration tensor by default:

 MEAN FIELD HOMOGENIZATION, ISOTROPIZATION=ALLISO

Use the following option to use the isotropic projection of the matrix stiffness to compute only Eshelby's tensor:

 MEAN FIELD HOMOGENIZATION, ISOTROPIZATION=E-ISO

Use the following option to use the isotropic projection of the matrix stiffness to compute Hill's tensor:

 MEAN FIELD HOMOGENIZATION, ISOTROPIZATION=P-ISO

Multi-step homogenization

For composites with multiple inclusions, a multi-step homogenization approach is used, as shown in Figure 2. The composite is decomposed into "grains," with each grain containing one inclusion family and the matrix. The inclusions in each family have the same material properties, aspect ratio, and orientation. In the first step homogenization is performed in each grain using the user-specified formulation; in the second step the Voigt formulation is used to compute the properties of the overall composite.

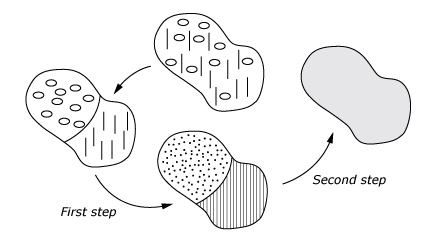
Figure 2. Multi-step homogenization method for multi-phase composites.

Specifying the microstructure of the composite

You can specify the microstructure of the composite by giving the shape, volume fraction, aspect ratio, and fiber orientation of each constituent. You can use a distribution to define the volume fraction, aspect ratio, and the orientation tensor (see Distribution definition).

Specifying the shape, volume fraction, and aspect ratio

The volume fraction and aspect ratio can be specified as spatial distributions. The aspect ratio is given by $D / L$ as shown in Figure 3.

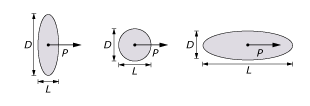
Figure 3. Different shapes of the inclusion.

The aspect ratio of a spherical inclusion is 1.0, and the aspect ratio of a cylindrical inclusion is infinity; therefore, you do not need to specify the aspect ratio in these cases.

Input File Usage

Use the following option to specify a prolate-shaped inclusion ( $L > D$ ):

CONSTITUENT, SHAPE=PROLATE
volume fraction, aspect ratio,

Use the following option to specify an oblate-shaped inclusion ( $L < D$ ):

CONSTITUENT, SHAPE=OBLATE
volume fraction, aspect ratio,

Use the following option to specify a penny-shaped inclusion ( $L ≪ D$ ):

CONSTITUENT, SHAPE=PENNY
volume fraction, aspect ratio,

Use the following option to specify a spherical inclusion:

CONSTITUENT, SHAPE=SPHERE
volume fraction,

Use the following option to specify a continuous cylindrical inclusion:

CONSTITUENT, SHAPE=CYLINDER
volume fraction,

Specifying a fixed fiber orientation

By default, the orientation of the inclusion is fixed and is aligned with the 1-direction of the local coordinate system specified in the section definition. You can specify a different direction by giving the three components of the fiber direction in the local coordinate system, as shown in Figure 4. The components of the orientation unit vector, $p$ , are

p_{1} = \sin θ \cos φ,

p_{2} = \sin θ \sin φ,

p_{3} = \cos θ .

Figure 4. Orientation of the inclusion.

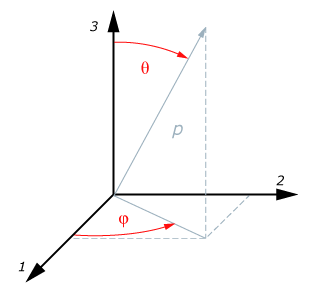
Input File Usage

Use the following option to specify a fixed fiber orientation:

CONSTITUENT, DIRECTION=FIXED
 ,  ,  $p_{1}, p_{2}, p_{3}$

Specifying a second-order orientation tensor

For composites containing short fibers, a second-order orientation tensor, $a,$ is usually used to describe the dispersion of the fiber orientation

a_{i j} = \oint p_{i} p_{j} Ψ (p) d p,

where $\oint d p = \int_{φ = 0}^{2 π} \int_{θ = 0}^{π} \sin θ d θ d φ$ is the integral over the surface of the unit sphere (all possible directions of $p$ ) and $Ψ (p)$ is the orientation distribution function (ODF). The spatial distribution of the orientation tensor is usually given by injection molding software and can be used directly to compute the effective moduli of the composite material that is linear elastic. If the material is nonlinear, the average fields given by $〈 f 〉 = \oint f (p) Ψ (p) d p$ must be computed during the analysis and the ODF is required to calculate the integral. When only the second-order orientation is available, Abaqus recovers the ODF using the approach proposed by Onat and Leckie (1988)

Ψ (p) ≃ \frac{1}{4 π} + \frac{15}{8 π} b_{i j} f_{i j} (p) + \frac{315}{32 π} B_{i j k l} F_{i j k l} (p),

for three-dimensional orientations, where $f_{i j}$ and $F_{i j k l}$ are the tensor basis functions

f_{i j} (p) = p_{i} p_{j} - \frac{1}{3} δ_{i j},

F_{i j k l}^{} = p_{i} p_{j} p_{k} p_{l} - \frac{1}{7} (p_{i} {p_{j} δ}_{k l} + {p_{i} p_{k}}_{} δ_{j l} + p_{i} p_{l} δ_{j k} + p_{k} p_{l} δ_{i j} + p_{j} p_{l} δ_{i k} + p_{j} p_{k} δ_{i l}) + \frac{1}{35} (δ_{i j} δ_{k l} + δ_{i k} δ_{j l} + δ_{i l} δ_{j k}),

and $b_{i j}$ and $B_{i j k l}$ are the deviatoric versions of the orientation tensors

b_{i j} = a_{i j} - \frac{1}{3} δ_{i j},

B_{i j k l}^{} = A_{i j k l} - \frac{1}{7} (a_{i j} δ_{k l} + a_{i k} δ_{j l} + a_{i l} δ_{j k} + a_{k l} δ_{i j} + a_{j l} δ_{i k} + a_{j k} δ_{i l}) + \frac{1}{35} (δ_{i j} δ_{k l} + δ_{i k} δ_{j l} + δ_{i l} δ_{j k}) .

The fourth-order orientation tensor is required during the ODF reconstruction. It is computed with the hybrid closure approximation proposed by Advani and Tucker (1987), which is constructed using the interpolation of linear and quadratic closure approximation

A_{i j k l}^{h} = (1 - α) A_{i j k l}^{l} + α A_{i j k l}^{q},

where the linear closure is given by

A_{i j k l}^{l} = - \frac{1}{35} (δ_{i j} δ_{k l} + δ_{i k} δ_{j l} + δ_{i l} δ_{j k}) + \frac{1}{7} (a_{i j} δ_{k l} + a_{i k} δ_{j l} + a_{i l} δ_{j k} + a_{k l} δ_{i j} + a_{j l} δ_{i k} + a_{j k} δ_{i l})

and the quadratic closure is given by

A_{i j k l}^{q} = a_{i j}^{} a_{k l} .

The weight function is defined as $α = 1 - 27 \det (a)$ for three-dimensional orientations.

Only one constituent in the composite is allowed to have orientations specified with the second-order orientation tensor.

Taking into account the symmetry of the ODF $Ψ (p) = Ψ (- p)$ , we compute the integral $\oint f (p) Ψ (p) d p$ numerically as follows:

\oint f (p) Ψ (p) d p ≃ {2 \sum}_{I = 1}^{N} \sum_{I = 1}^{N} f (θ_{I}, φ_{J}) Ψ (θ_{I}, φ_{J}) \sin (θ_{I}) Δ θ Δ φ,

where $Δ θ = Δ φ = \frac{π}{N}$ and $θ_{I} = I Δ θ, φ_{J} = J Δ φ$ . The numerical integral is computed by subdividing the macro point into $N \times N$ subdomains, with each subdomain having the same fiber orientation $p = p (θ_{I}, φ_{J})$ . Then a multi-step homogenization (as described in Figure 2) is used to compute the macro-level solutions. The ODF is more accurately recovered if a large value of N is used; however, the computational cost and memory usage also increases substantially.

Input File Usage

Use the following option to specify the fiber orientation using a second-order tensor:

CONSTITUENT, DIRECTION=ORIENTATION TENSOR
 , ,  $a_{11}, a_{22}, a_{33}, a_{12}, a_{13}, a_{23}$

Use the following option to specify the number of subdivisions used to compute the surface integral:

MEAN FIELD HOMOGENIZATION, ANGLE SUBDIVISIONS=N

Composites with thermal expansion

A three-step approach is used to compute the macro response of a thermo-elastic composite (Pierard, 2004). The total macro strain is applied to the composite in the first step with no temperature change. The strain in each constituent is computed with the concentration tensor, and the stress is updated accordingly. In Step 2 an equal temperature change is applied to all constituents; by assuming uniform stress increment in all constituents, the strain increment in the second step is computed in each constituent. In Step 3 an equal and opposite strain increment computed in Step 2 is applied to all constituents to recover the total macro strain; there is no temperature change in this step. The total strain and stress in each constituent is computed by superposing the solutions from all three steps. This approach is also applied to the incremental formulation of nonlinear composites with thermal expansion.

Example

This simple example illustrates how to define a multiscale material.

The name of the multiscale material is COMPOSITE. The material consists of one inclusion material MAT2 embedded in the matrix material MAT1. The shape of the inclusion is prolate. The Mori-Tanaka homogenization method is used. The inclusion has a volume fraction of $v_{f}^{}$ and an aspect ratio of $a r$ . The direction of the inclusion is fixed and defined with a vector $(p_{1}, p_{2}, p_{3})$ . The name of the matrix is MATRIX_MAT1, and the name of the inclusion is FIBER_MAT2.

Input file template

MATERIAL, NAME=MAT1
…
MATERIAL, NAME=MAT2
…
MATERIAL, NAME=COMPOSITE
MEAN FIELD HOMOGENIZATION, FORMULATION=MT
CONSTITUENT, TYPE=MATRIX, MATERIAL=MAT1, NAME=MATRIX_MAT1
CONSTITUENT, TYPE=INCLUSION, MATERIAL=MAT2, NAME=FIBER_MAT2, SHAPE=PROLATE, DIRECTION=FIXED
 $v_{f}^{}$ ,  $a r$ ,  $p_{1}$ ,  $p_{2}$ ,  $p_{3}$

Elements

The multiscale material model can be used only with three-dimensional pure stress/displacement solid elements in Abaqus/Standard.

Output

By default, the output variables are macro-level results. For field output you can also request micro-level output. The name of the constituent is appended to the end of the output variable.

Input File Usage

Use the following options to request field output for the constituents:

OUTPUT, FIELD
ELEMENT OUTPUT, MICROMECHANICS

References

Eshelby, J. D., “The Determination of the Elastic Field of an Ellipsoidal Inclusion and Related Problems,” Proceedings of the Royal Society of London, pp. 376–396, 1957.
Advani, S., and C. Tucker, “The User of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites,” Journal of Rheology, vol. 31 (8), pp. 751–784, 1987.
Onat, E.T., and F.A. Leckie, “Representation of Mechanical Behavior in the Presence of Changing Internal Structure,” Journal of Applied Mechanics, vol. 55(1), pp. 1–10, 1988.
Mura, T., Micromechanics of Defects in Solids, MARTINUS NIJHOFF Publishers, 1987.
Pierard, O., C. Friebel, and I. Doghri, “Mean-Field Homogenization of Multi-Phase Thermo-Elastic Composites: a General Framework and its Validation,” Composites Science and Technology, vol. 64, pp. 1587–1603, 2004.
Pierard, O., and I. Doghri, “An Enhanced Affine Formulation and the Corresponding Numerical Algorithms for the Mean-Field Homogenization of Elasto-Viscoplastic Composites,” International Journal of Plasticity, pp. 131–157, 2006.
Doghri, I., and A. Ouaar, “Homogenization of Two-Phase Elasto-Plastic Composite Materials and Structures. Study of Tangent Operators, Cyclic Plasticity and Numerical Algorithms,” International Journal of Solids and Structures, vol. 40(7), pp. 1681–1712, 2003.
Selmi, A., I. Doghri, and L. Adam, “Micromechanical Simulations of Biaxial Yield, Hardening and Plastic Flow in Short Glass Fiber Reinforced Polyamide,” International Journal of Mechanical Sciences, vol. 53(9), pp. 696–706, 2011.
Doghri, I., I. Adam, and N. Bilger, “Mean-Field Homogenization of Elasto-Viscoplastic Composites Based on a General Incrementally Affine Linearization Method,” International Journal of Plasticity, pp. 219–238, 2010.
Kammoun, S., L. Brassart, G. Robert, I. Doghri, and L. Delannay, “Micromechanical Modeling of Short Glass-Fiber Reinforced Thermoplastics-Isotropic Damage of Pseudograins,” American Institute of Physics Conference Proceedings 1353, pp. 974–977, 2011.
Lielens, G., “Micro-Macro Modeling of Structured Materials,” PhD Thesis Universite Catholique de Louvain Belgium, 1999.