Multiscale material modeling

The multiscale material model in Abaqus/Standard uses the mean-field homogenization approach to capture the behavior of heterogeneous materials that contain a matrix material and one or more inclusion materials.

The goal of multiscale material modeling is to predict material behaviors at the macro-level using information at smaller scales. The information can be communicated between scales from the bottom up; the microstructure of the composite material is represented by a Representative Volume Element (RVE), then a homogenization scheme is applied to the RVE, which provides a prediction of macro-constitutive behavior at a material point, as shown in Figure 1.

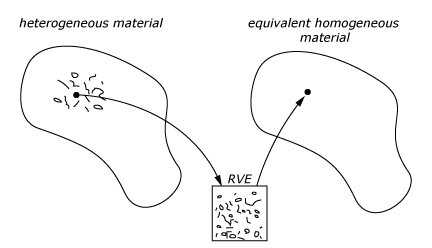
Figure 1. Homogenization of a heterogeneous material.

The information can also be communicated from a macro scale down to smaller scales by applying the macro-strain as a far-field strain to the RVE. The state of the constituents on the micro-level, such as strain and stress, are then updated, and the averaged quantities are communicated back to the material point at the macro-level.

Mean-field homogenization is based on analytical models of a single inclusion problem, and it gives an approximation of the averaged stresses and strains in each constituent of the composite. The averaged strain of each constituent is determined based on the specific homogenization method, which is based on assumptions of the interaction between inclusions and the matrix. Since only volume-averaged quantities are considered, this approach is unable to capture local stress concentration inside the RVE and the size effects of the inclusions; however, it is computationally efficient compared to the FE-RVE approach in which the RVE is modeled with a finite element model.

The mean-field homogenization approach gives good predictions for linear elastic composites. Since the homogenization is performed during the analysis, nonlinear and history-dependent behavior can be captured. However, in the case of highly nonlinear constituent materials, calibration is usually necessary for better predictions. If experimental results are not available, the results of an FE-RVE that represent details of the microstructure can be used as an alternative for calibration.