Using a general beam section to define the section behavior

Linear section behavior

Linear section response is calculated as follows. At each point in the cross-section the axial stress, $σ$ , and the shear stress, $τ$ , are given by

σ = E (\bar{θ}, f_{β}) (ε - ε^{t h}) and τ = G (\bar{θ}, f_{β}) γ,

where

$E (\bar{θ}, f_{β})$: is Young's modulus (which may depend on the temperature, $\bar{θ}$ , and field variables, $f_{β}$ , at the beam axis);
$G (\bar{θ}, f_{β})$: is the shear modulus (which may also depend on the temperature and field variables at the beam axis);
$ε$: is the axial strain;
$γ$: is the shear caused by twist; and
$ε^{t h}$: is the thermal expansion strain.

The thermal expansion strain is given by

ε^{t h} = α (\bar{θ}, f_{β}) (θ - θ^{0}) - α ({\bar{θ}}^{I}, f_{β}^{I}) (θ^{I} - θ^{0}),

where

$α (\bar{θ}, f_{β})$: is the thermal expansion coefficient,
$θ$: is the current temperature at a point in the beam section,
$f_{β}$: are field variables,
$θ^{0}$: is the reference temperature for $α$ ,
$θ^{I}$: is the initial temperature at this point (see Defining initial temperatures), and
$f_{β}^{I}$: are the initial values of the field variables at this point (see Defining initial values of predefined field variables).

If the thermal expansion coefficient is temperature or field-variable dependent, it is evaluated at the temperature and field variables at the beam axis. Therefore, since we assume that $θ$ varies linearly over the section, $ε^{t h}$ also varies linearly over the section.

The temperature is defined from the temperature of the beam axis and the gradients of temperature with respect to the local $x_{1}$ - and $x_{2}$ -axes:

θ = \bar{θ} + \frac{\partial θ}{\partial x_{1}} x_{1} + \frac{\partial θ}{\partial x_{2}} x_{2} .

The axial force, N; bending moments, $M_{1}$ and $M_{2}$ about the 1 and 2 beam section local axes; torque, T; and bimoment, W, are defined in terms of the axial stress $σ$ and the shear stress $τ$ (see Beam element formulation). These terms are

\begin{matrix} N = & E (A (ε_{c} - ε_{c}^{t h}) + Γ_{0} χ), \\ M_{1} = & E (I_{11} (κ_{1} - \frac{\partial ε^{t h}}{\partial x_{2}}) - I_{12} (κ_{2} + \frac{\partial ε^{t h}}{\partial x_{1}})), \\ M_{2} = & E (- I_{12} (κ_{1} - \frac{\partial ε^{t h}}{\partial x_{2}}) + I_{22} (κ_{2} + \frac{\partial ε^{t h}}{\partial x_{1}})), \\ T = & G J ϕ + G I_{p} w_{p}, \\ W = & E (Γ_{0} (ε_{c} - ε_{c}^{t h}) + Γ_{W} χ), \end{matrix}

where

A: is the area of the section,
$I_{11}$: is the moment of inertia for bending about the 1-axis of the section,
$I_{12}$: is the moment of inertia for cross-bending,
$I_{22}$: is the moment of inertia for bending about the 2-axis of the section,
J: is the torsional constant,
$Γ_{0}$: is the sectorial moment of the section,
$Γ_{W}$: is the warping constant of the section,
$ε_{c}$: is the axial strain measured at the centroid of the section,
$ε_{c}^{t h}$: is the thermal axial strain,
$κ_{1}$: is the curvature change about the first beam section local axis,
$κ_{2}$: is the curvature change about the second beam section local axis,
$ϕ$: is the twist,
$χ$: is the bicurvature defining the axial strain in the section due to the twist of the beam, and
$w_{p} = w_{f} - w$: is the difference between the unconstrained warping amplitude, $w_{f}$ , and the actual warping amplitude, w.

$Γ_{0}$ , $Γ_{W}$ , $χ$ , and $w_{p}$ are nonzero only for open-section beam elements.

Defining linear section behavior for library cross-sections or linear generalized cross-sections

Linear beam section response is defined geometrically by A, $I_{11}$ , $I_{12}$ , $I_{22}$ , J, and—if necessary— $Γ_{0}$ and $Γ_{W}$ .

You can input these geometric quantities directly or specify a standard library section and Abaqus will calculate these quantities. In either case define the orientation of the beam section (see Beam element cross-section orientation); give Young's modulus, the torsional shear modulus, and the coefficient of thermal expansion, as functions of temperature; and associate the section properties with a region of your model.

If the thermal expansion coefficient is temperature dependent, the reference temperature for thermal expansion must also be defined as described later in this section.

Specifying the geometric quantities directly

You can define “generalized” linear section behavior by specifying A, $I_{11}$ , $I_{12}$ , $I_{22}$ , J, and—if necessary— $Γ_{0}$ and $Γ_{W}$ directly. In this case you can specify the location of the centroid, thus allowing the bending axis of the beam to be offset from the line of its nodes. In addition, you can specify the location of the shear center.

Input File Usage

Use the following option to define generalized linear beam section properties:

BEAM GENERAL SECTION, SECTION=GENERAL, ELSET=name
A,  $I_{11}$ ,  $I_{12}$ ,  $I_{22}$ , J,  $Γ_{0}$ ,  $Γ_{W}$

If necessary, use the following option to specify the location of the centroid:

CENTROID

If necessary, use the following option to specify the location of the shear center:

SHEAR CENTER

Abaqus/CAE Usage

Property module:
Create Profile: Name: generalized_section, Generalized
Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis, Profile name: generalized_section: Centroid and Shear Center
AssignSection: select regions

Specifying a standard library section and allowing Abaqus to calculate the geometric quantities

You can select one of the standard library sections (see Beam cross-section library) and specify the geometric input data needed to define the shape of the cross-section. Abaqus will then calculate the geometric quantities needed to define the section behavior automatically. In addition, you can specify an offset for the section origin.

Input File Usage

BEAM GENERAL SECTION, SECTION=library_section, ELSET=name

If necessary, use the following option to specify an offset for the section origin:

BEAM SECTION OFFSET

Abaqus/CAE Usage

Property module:
Create Profile: Name: library_section
Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis, Profile name: library_section
AssignSection: select regions

Specifying an offset for the section origin is not supported in Abaqus/CAE.

Defining linear section behavior for meshed cross-sections

Linear beam section response for a meshed section profile is obtained by numerical integration from the two-dimensional model. The numerical integration is performed once, determining the beam stiffness and inertia quantities, as well as the coordinates of the centroid and shear center, for the duration of the analysis. These beam section properties are calculated during the beam section generation and are written to the text file jobname.bsp. This text file can be included in the beam model. See Meshed beam cross-sections for a detailed description of the properties defining the linear beam section response for a meshed section, as well as for how a typical meshed section is analyzed.

Input File Usage

Use the following options:

BEAM GENERAL SECTION, SECTION=MESHED, ELSET=name
INCLUDE, INPUT=jobname.bsp

Abaqus/CAE Usage

Meshed cross-sections are not supported in Abaqus/CAE.

Defining linear section behavior for tapered cross-sections in Abaqus/Standard

In Abaqus/Standard you can define Timoshenko beams with linearly tapered cross-sections. General beam sections with linear response and standard library sections are supported, with the exception of arbitrary sections. The section parameters are defined at the two end nodes of each beam element. The effective beam area and moment of inertia for bending about the 1- and 2-axis of the section used in the calculation of the beam stiffness matrix, section forces, and stresses are

\begin{matrix} A^{eff} = & \frac{A^{I} + \sqrt{A^{I} A^{J}} + A^{J}}{3}, \\ I_{11}^{eff} = & \frac{I_{11}^{I} + \sqrt[4]{{(I_{11}^{I})}^{3} I_{11}^{J}} + \sqrt{I_{11}^{I} I_{11}^{J}} + \sqrt[4]{I_{11}^{I} {(I_{11}^{J})}^{3}} + I_{11}^{J}}{5}, \\ I_{22}^{eff} = & \frac{I_{22}^{I} + \sqrt[4]{{(I_{22}^{I})}^{3} I_{22}^{J}} + \sqrt{I_{22}^{I} I_{22}^{J}} + \sqrt[4]{I_{22}^{I} {(I_{22}^{J})}^{3}} + I_{22}^{J}}{5}, \end{matrix}

where the superscripts $I$ and $J$ refer to the two end nodes of the beam. The remaining effective geometric quantities are calculated as the average between the values at the two end nodes. This approximation suffices for mild tapering along each element, but it can lead to large errors if the tapering is not gradual. Abaqus/Standard issues a warning message during input file preprocessing if the area or inertia ratio is larger than 2.0 and an error message if the ratio is larger than 10.0.

The effective area and inertia are not used in the computation of the mass matrix. Instead, terms on the diagonal quadrants use the properties from the respective nodes, while off-diagonal quadrants use averaged quantities. For example, the axial inertia a linear element would have the diagonal term coming from node $I$ of $ρ A^{I} / 3$ , while node $J$ contributes with $ρ A^{J} / 3$ and the two off-diagonal contributions equal $ρ (A^{I} + A^{J}) / 12$ . Mild tapering is assumed in this formulation, since the total mass of the element totals $ρ (A^{I} + A^{J}) / 2$ .

Note:

When you apply a tapered beam section to geometry in Abaqus/CAE, the full tapering is applied to each element along the beam’s length. For beams that include multiple elements, this modeling style can create a sawtooth pattern along the length of the beam. If you want to model gradual tapering along the entire length of the beam in Abaqus/CAE, you must calculate the size and shape of the beam profiles at the intermediate nodes, then apply different tapered beam sections to each beam element along the length.

Input File Usage

Use the following option to define linear section behavior of tapered cross-sections:

BEAM GENERAL SECTION, TAPER, ELSET=name

Abaqus/CAE Usage

Property module:
Create Profile: Name: library_section
Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis, Beam shape along length: Tapered: Beam start and Beam end options: Profile name: library_section
AssignSection: select regions

Nonlinear section behavior

Typically nonlinear section behavior is used to include the experimentally measured nonlinear response of a beam-like component whose section distorts in its plane. When the section behaves according to beam theory (that is, the section does not distort in its plane) but the material has nonlinear response, it is usually better to use a beam section integrated during the analysis to define the section geometrically (see Using a beam section integrated during the analysis to define the section behavior), in association with a material definition.

Nonlinear section behavior can also be used to model beam section collapse in an approximate sense: Nonlinear dynamic analysis of a structure with local inelastic collapse illustrates this for the case of a pipe section that may suffer inelastic collapse due to the application of a large bending moment. In following this approach you should recognize that such unstable section collapse, like any unstable behavior, typically involves localization of the deformation: results will, therefore, be strongly mesh sensitive.

Calculation of nonlinear section response

Nonlinear section response is assumed to be defined by

\begin{matrix} N = & N (ε_{c} - ε_{c}^{t h}, \bar{θ}, f_{β}), \\ M_{1} = & M_{1} (κ_{1}, \bar{θ}, f_{β}), \\ M_{2} = & M_{2} (κ_{2}, \bar{θ}, f_{β}), \\ T = & T (ϕ, \bar{θ}, f_{β}), \end{matrix}

where $()$ means a functional dependence on the conjugate variables: $N = N (ε)$ , $M_{1} = M_{1} (κ_{1})$ , etc. For example, $N (ε_{c} - ε_{c}^{t h}, \bar{θ}, f_{β})$ means that N is a function of: $ε_{c} - ε_{c}^{t h}$ ; $\bar{θ}$ , the temperature of the beam axis; and of $f_{β}$ , any predefined field variables at the beam axis. When the section behavior is defined in this way, only the temperature and field variables of the beam axis are used: any temperature or field-variable gradients given across the beam section are ignored.

These nonlinear responses may be purely elastic (that is, fully reversible—the loading and unloading responses are the same, even though the behavior is nonlinear) or may be elastic-plastic and, therefore, irreversible.

The assumption that these nonlinear responses are uncoupled is restrictive; in general, there is some interaction between these four behaviors, and the responses are coupled. You must determine if this approximation is reasonable for a particular case. The approach works well if the response is dominated by one behavior, such as bending about one axis. However, it may introduce additional errors if the response involves combined loadings.

Defining nonlinear section behavior

You can define “generalized” nonlinear section behavior by specifying the area, A; moments of inertia, $I_{11}$ for bending about the 1-axis of the section, $I_{22}$ for bending about the 2-axis of the section, and $I_{12}$ for cross-bending; and torsional constant, J. These values are used only to calculate the transverse shear stiffness; and, if needed, A is used to compute the mass density of the element. In addition, you can define the orientation and the axial, bending, and torsional behavior of the beam section (N, $M_{1}$ , $M_{2}$ , T), as well as the thermal expansion coefficient. If the thermal expansion coefficient is temperature dependent, the reference temperature for thermal expansion must also be defined as described below.

Nonlinear generalized beam section behavior cannot be used with beam elements with warping degrees of freedom.

The axial, bending, and torsional behavior of the beam section and the thermal expansion coefficient are defined by tables. See Material data definition for a detailed discussion of the tabular input conventions. In particular, you must ensure that the range of values given for the variables is sufficient for the application since Abaqus assumes a constant value of the dependent variable outside this range.

Input File Usage

Use the following options to define generalized nonlinear beam section properties:

BEAM GENERAL SECTION, SECTION=NONLINEAR GENERAL, 
ELSET=name
A,  $I_{11}$ ,  $I_{12}$ ,  $I_{22}$ , J
AXIAL for N
M1 for  $M_{1}$ 
M2 for  $M_{2}$ 
TORQUE for T
THERMAL EXPANSION for the thermal expansion coefficient

Abaqus/CAE Usage

Nonlinear generalized cross-sections are not supported in Abaqus/CAE.

Defining linear response for N, M₁, M₂, and T

If the particular behavior is linear, N, $M_{1}$ , $M_{2}$ , and T should be specified as functions of the temperature and predefined field variables, if appropriate.

As an example of axial behavior, if

N = (A E) (ε_{c} - ε_{c}^{t h}),

where $(A E)$ is constant for a given temperature, the value of $(A E)$ is entered. $(A E)$ can still be varied as a function of temperature and field variables.

Input File Usage

Use the following options to define linear axial, bending, and torsional behavior:

AXIAL, LINEAR
M1, LINEAR
M2, LINEAR
TORQUE, LINEAR

Abaqus/CAE Usage

Nonlinear generalized cross-sections are not supported in Abaqus/CAE.

Defining nonlinear elastic response for N, M₁, M₂, and T

If the particular behavior is nonlinear but elastic, the data should be given from the most negative value of the kinematic variable to the most positive value, always giving a point at the origin. See Figure 1 for an example.

Input File Usage

Use the following options to define nonlinear elastic axial, bending, and torsional behavior:

AXIAL, ELASTIC
M1, ELASTIC
M2, ELASTIC
TORQUE, ELASTIC

Abaqus/CAE Usage

Nonlinear generalized cross-sections are not supported in Abaqus/CAE.

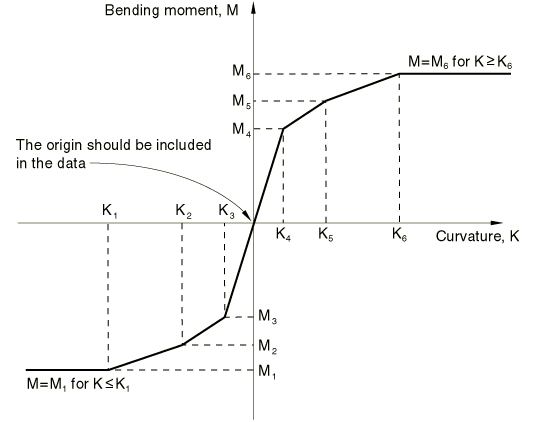
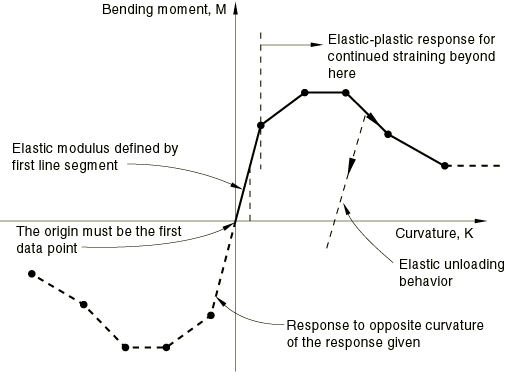
Figure 1. Example of elastic nonlinear beam section behavior definition.

Defining elastic-plastic response for N, M₁, M₂, and T

By default, elastic-plastic response is assumed for N, $M_{1}$ , $M_{2}$ , and T.

The inelastic model is based on assuming linear elasticity and isotropic hardening (or softening) plasticity. The data in this case must begin with the $(0, 0)$ point and proceed to give positive values of the kinematic variable at increasing positive values of the conjugate force or moment. Strain softening is allowed. The elastic modulus is defined by the slope of the initial line segment, so that straining beyond the point that terminates that initial line segment will be partially inelastic. If strain reversal occurs in that part of the response, it will be elastic initially. See Figure 2 for an example.

Input File Usage

Use the following options to define elastic-plastic axial, bending, and torsional behavior:

AXIAL
M1
M2
TORQUE

Abaqus/CAE Usage

Nonlinear generalized cross-sections are not supported in Abaqus/CAE.

Figure 2. Example of inelastic nonlinear beam section behavior definition.

Defining the reference temperature for thermal expansion

The thermal expansion coefficient may be temperature dependent. In this case the reference temperature for thermal expansion, $θ^{0}$ , must be defined.

Input File Usage

BEAM GENERAL SECTION, ZERO= $θ^{0}$

Abaqus/CAE Usage

Property module: Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis: Basic: Specify reference temperature:  $θ^{0}$

Defining the initial section forces and moments

You can define initial stresses (see Defining initial stresses) for general beam sections that will be applied as initial section forces and moments. Initial conditions can be specified only for the axial force, the bending moments, and the twisting moment. Initial conditions cannot be prescribed for the transverse shear forces.

Defining a change in cross-sectional area due to straining

In the shear flexible elements Abaqus provides for a possible uniform cross-sectional area change by allowing you to specify an effective Poisson's ratio for the section. This effect is considered only in geometrically nonlinear analysis (see Defining an analysis) and is provided to model the reduction or increase in the cross-sectional area for a beam subjected to large axial stretch.

The value of the effective Poisson's ratio must be between −1.0 and 0.5. By default, this effective Poisson's ratio for the section is set to 0.0 so that this effect is ignored. Setting the effective Poisson's ratio to 0.5 implies that the overall response of the section is incompressible. This behavior is appropriate if the beam is made of rubber or if it is made of a typical metal whose overall response at large deformation is essentially incompressible (because it is dominated by plasticity). Values between 0.0 and 0.5 mean that the cross-sectional area changes proportionally between no change and incompressibility, respectively. A negative value of the effective Poisson's ratio will result in an increase in the cross-sectional area in response to tensile axial strains.

This effective Poisson's ratio is not available for use with Euler-Bernoulli beam elements.

Input File Usage

BEAM GENERAL SECTION, POISSON= $ν_{eff}$

Abaqus/CAE Usage

Property module: Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis: Basic: Section Poisson's ratio:  $ν_{eff}$

Defining damping

When the beam section and material behavior are defined by a general beam section, you can include mass and viscous stiffness proportional damping in the dynamic response (calculated in Abaqus/Standard with the direct time integration procedure, Implicit dynamic analysis using direct integration).

See Material damping for more information about the material damping types available in Abaqus.

Input File Usage

Use both of the following options:

BEAM GENERAL SECTION
DAMPING

Abaqus/CAE Usage

Property module: Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis: Damping: Alpha, Beta, Structural, and Composite

Specifying temperature and field variables

Define temperatures and field variables by giving the values at the origin of the cross-section as either predefined fields or initial conditions (see Predefined Fields or Initial conditions in Abaqus/Standard and Abaqus/Explicit). Temperature gradients can be specified in the local 1- and 2-directions; other field-variable gradients defined through the cross-section will be ignored in the response of beam elements that use a general beam section definition.

Output

Only the section forces, moments, and transverse shear forces and section strains, curvatures, and transverse shear strains can be output (see Element output and Element output).

You can output stress and strain at particular points in the section. For linear section behavior defined using a standard library section or a generalized section, only axial stress and axial strain values are available. For linear section behavior defined using a meshed section, axial and shear stress and strain are available. For nonlinear generalized section behavior, axial strain output only is provided.

Specifying the output section points for standard library sections and generalized sections

To locate points in the section at which output of axial strain (and, for linear section behavior, axial stress) is required, specify the local $(x_{1}, x_{2})$ coordinates of the point in the cross-section: Abaqus numbers the points 1, 2, … in the order that they are given.

The variation of $ε$ over the section is given by

ε = ε_{c} + κ_{1} (x_{2} - x_{2 c}) - κ_{2} (x_{1} - x_{1 c}),

where $(x_{1 c}, x_{2 c})$ are the local coordinates of the centroid of the beam section and $κ_{1}$ and $κ_{2}$ are the changes of curvature for the section.

For open-section beam element types, the variation of $ε$ over the section has an additional term of the form $ψ (x_{1}, x_{2}) χ$ , where $ψ (x_{1}, x_{2})$ is the warping function. The warping function itself is undefined in the general beam section definition. Therefore, Abaqus will not take into account the axial strain due to warping when calculating section points output. Axial strains due to warping are included in the stress/strain output if a beam section integrated during the analysis is used.

Abaqus uses St. Venant torsion theory for noncircular solid sections. The torsion function and its derivatives are necessary to calculate shear stresses in the plane of the cross-section. The function and its derivatives are not stored for a general beam section. Therefore, you can request output of axial components of stress/strain only. A beam section integrated during the analysis must be used to obtain output of shear stresses.

Input File Usage

Use both of the following options to specify the output section points for general beam sections:

BEAM GENERAL SECTION
SECTION POINTS
 $x_{1}$ ,  $x_{2}$ , ...

Abaqus/CAE Usage

Property module: Create Section: select Beam as the section Category and Beam as the section Type: Section integration: Before analysis: Output Points: x1, x2, ...

Requesting output of maximum axial stress/strain in Abaqus/Standard

If you specify the output section points to obtain the maximum axial stress/strain (MAXSS) for a linear generalized section, the output value will be the maximum of the values at the user-specified section points. You must select enough section points to ensure that this is the true maximum. MAXSS output is not available for nonlinear generalized sections or for an Abaqus/Explicit analysis.

Specifying the output section points for meshed cross-sections

For meshed cross-sections you can indicate in the two-dimensional cross-section analysis the elements and integration points where the stress and strain will be calculated during the subsequent beam analysis. Abaqus will then add the section points specification to the resulting jobname.bsp text file. This text file is then included as the data for the general beam section definition in the subsequent beam analysis. See Meshed beam cross-sections for details.

The variation of the axial strain $ε$ over the meshed section is given by

ε = ε_{c} + κ_{1} (x_{2} - x_{2 c}) - κ_{2} (x_{1} - x_{1 c}),

where $(x_{1 c}, x_{2 c})$ are the local coordinates of the centroid of the beam section and $κ_{1}$ and $κ_{2}$ are the changes of curvature for the section.

The variations of shear components $γ_{1}$ and $γ_{2}$ over the meshed section are given by

γ_{1} = γ_{s 1} + ϕ (\frac{\partial Ψ}{\partial x_{1}} - (x_{2} - x_{2 s})),

γ_{2} = γ_{s 2} + ϕ (\frac{\partial Ψ}{\partial x_{2}} + (x_{1} - x_{1 s})),

where $(x_{1 s}, x_{2 s})$ are the local coordinates of the shear center of the beam section, $ϕ$ is the twist of the beam axis, $Ψ (x_{1}, x_{2})$ is the warping function, and $γ_{s 1}$ and $γ_{s 2}$ are shear strains due to the transverse shear forces.

For the case of an orthotropic composite beam material, the axial stress $σ$ and the two shear components $τ_{1}$ and $τ_{2}$ are calculated in the beam section (1, 2) axis as follows:

{\begin{matrix} σ \\ τ_{1} \\ τ_{2} \end{matrix}} = [\begin{matrix} E & 0 & 0 \\ G_{1} {(\cos α)}^{2} + G_{2} {(\sin α)}^{2} & (G_{1} - G_{2}) \cos α \sin α \\ s y m & G_{1} {(\sin α)}^{2} + G_{2} {(\cos α)}^{2} \end{matrix}] {\begin{matrix} ε \\ γ_{1} \\ γ_{2} \end{matrix}},

where $α$ determines the material orientation.

Input File Usage

Use both of the following options in the two-dimensional meshed cross-section analysis to specify the output section points for the subsequent beam analysis:

BEAM SECTION GENERATE
SECTION POINTS
section_point_label, element_number, integration_point_number

Abaqus/CAE Usage

Meshed cross-sections are not supported in Abaqus/CAE.

Using a general beam section to define the section behavior

Linear section behavior

Defining linear section behavior for library cross-sections or linear generalized cross-sections

Specifying the geometric quantities directly

Specifying a standard library section and allowing Abaqus to calculate the geometric quantities

Defining linear section behavior for meshed cross-sections

Defining linear section behavior for tapered cross-sections in Abaqus/Standard

Nonlinear section behavior

Calculation of nonlinear section response

Defining nonlinear section behavior

Defining linear response for N, M1, M2, and T

Defining nonlinear elastic response for N, M1, M2, and T

Defining elastic-plastic response for N, M1, M2, and T

Defining the reference temperature for thermal expansion

Defining the initial section forces and moments

Defining a change in cross-sectional area due to straining

Defining damping

Specifying temperature and field variables

Output

Specifying the output section points for standard library sections and generalized sections

Requesting output of maximum axial stress/strain in Abaqus/Standard

Specifying the output section points for meshed cross-sections

Defining linear response for N, M₁, M₂, and T

Defining nonlinear elastic response for N, M₁, M₂, and T

Defining elastic-plastic response for N, M₁, M₂, and T