Connector elastic behavior

In the simplest case of linear uncoupled elasticity you define the spring stiffnesses for the selected components (i.e., $D_{11}$ for component 1, $D_{22}$ for component 2, etc.), which are used in the equation

where $F_i$ is the force or moment in the $i^{\mathrm{th}}$ component of relative motion and $u_i$ is the connector displacement or rotation in the $i^{\mathrm{th}}$ direction. The elastic stiffness can depend on frequency (in Abaqus/Standard), temperature, and field variables. See Input Syntax Rules for further information about defining data as functions of frequency, temperature, and field variables.

In most cases if frequency-dependent damping behavior is specified in an Abaqus/Standard analysis procedure, the data at zero frequency is used. The exceptions are direct-solution steady-state dynamics, subspace-based steady-state dynamics, and natural or complex eigenvalue extraction.

CONNECTOR BEHAVIOR, NAME=name
CONNECTOR ELASTICITY, COMPONENT=component number, 
DEPENDENCIES=n

Interaction module: connector section editor: AddElasticity: Definition: Linear, Force/Moment: component or components, Coupling: Uncoupled

In the linear coupled case you define the spring stiffness matrix components, $D_{ij}$, which are used in the equation

where $F_i$ is the force in the $i^{\mathrm{th}}$ component of relative motion, $u_j$ is the motion of the $j^{\mathrm{th}}$ component, and $D_{ij}$ is the coupling between the $i^{\mathrm{th}}$ and $j^{\mathrm{th}}$ components. The D matrix is assumed to be symmetric, so only the upper triangle of the matrix is specified. In connectors with kinematic constraints the entries that correspond to the constrained components of relative motion will be ignored. The elastic stiffness can depend on temperature and field variables. See Input Syntax Rules for further information about defining data as functions of temperature and field variables.

CONNECTOR BEHAVIOR, NAME=name
CONNECTOR ELASTICITY, DEPENDENCIES=n

Interaction module: connector section editor: AddElasticity: Definition: Linear, Force/Moment: component or components, Coupling: Coupled

By definition, linear elastic behavior should be defined by a symmetric spring stiffness matrix. However, Abaqus/Standard allows you to define an unsymmetric coupled spring stiffness matrix. The intended use case is to approximate fluid film bearings supporting a rotating structure in a rotordynamic analysis (see Genta, 2005, and Distributed loads). Abaqus/Standard will not check the stability of an unsymmetric spring stiffness matrix; therefore, you must ensure that it is defined properly.

In the linear coupled case you define the spring stiffness matrix components, $D_{ij}$, which are used in the equation

where $F_i$ is the force in the $i^{\mathrm{th}}$ component of relative motion, $u_j$ is the motion of the $j^{\mathrm{th}}$ component, and $D_{ij}$ is the coupling between the $i^{\mathrm{th}}$ and $j^{\mathrm{th}}$ components. The D matrix in this case is assumed to be unsymmetric, so the entire matrix is specified. The entries that correspond to the constrained components of relative motion are ignored. When the unsymmetric matrix storage and solution scheme are used, the stiffness can depend on frequency, temperature, and field variables. See Input Syntax Rules for further information about defining data as functions of frequency, temperature and field variables.

CONNECTOR BEHAVIOR, NAME=name
CONNECTOR ELASTICITY, UNSYMM, 
FREQUENCY DEPENDENCE=ON

For nonlinear elasticity you specify forces or moments as nonlinear functions of one or more available components of relative motion, $F_i\left(u_1,u_2,\mathrm{\dots }\right)$. These functions can also depend on temperature and field variables. See Input Syntax Rules for further information about defining data as functions of temperature and field variables.

The combined connector in Figure 1 has two available components of relative motion: the relative displacement along the 1-direction (from the SLOT connection) and the rotation around the 1-direction (from the REVOLUTE connection)—see SLOT and REVOLUTE. Thus, the connector components of relative motion 1 and 4 can be used to specify connector behavior.

Figure 1. Simplified connector model of a shock absorber.

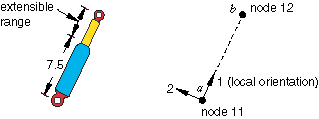
To define a nonlinear torsional spring to resist the relative rotation between the top and the bottom connection point around the local 1-direction, use the following input:

CONNECTOR SECTION, ELSET=shock, BEHAVIOR=sbehavior
slot, revolute
ori,
CONNECTOR BEHAVIOR, NAME=sbehavior
CONNECTOR ELASTICITY, COMPONENT=4, NONLINEAR 
-900., -0.7
   0.,  0.0
1250.,  0.7

Although no elastic coupling is assumed to occur between the two available components of relative motion, you could replace the nonlinear moment versus rotation data with coupled linear elastic behavior to define the rotational stiffness around the shock's axis coupled to the axial displacement.

In another application this same connector may have coupled linear elastic behavior, in the sense that relative rotation and sliding affect each other through a linear coupling. To define a translational stiffness of 2000.0 units, the $D_{11}$ constant (the 1st entry of a symmetric matrix) is entered in the connector elasticity definition. To define a torsional stiffness of 1000.0 units, the $D_{44}$ constant (the 10th entry of a symmetric matrix) is entered; and to define a coupling stiffness of 50.0 units between the available rotation and displacement, the $D_{14}$ constant (the 7th entry) is entered.

CONNECTOR ELASTICITY
2000.0, , , , , , 50.0,
0.0, 1000.0, , , , , ,
, , , ,

Rigid-like elastic connector behavior can be used to make an otherwise available component of relative motion rigid. Consider a CARTESIAN connector that has no intrinsic kinematic constraints. If rigid behavior is specified in the local 2- and 3-directions, the connector will behave in a similar fashion to a SLOT connector.

This technique of using connectors with available components of relative motion for which rigid behavior is specified instead of connectors with intrinsically kinematic constraints is particularly useful when you need to:

• customize the constrained components in a connector with available components of relative motion; for example, you can constrain the local 1- and 2-directions in a CARTESIAN connector to define a SLOT-like connector in the 3-direction;

• define rigid plastic behavior (see Connector plastic behavior); or

• define rigid damage behavior (see Connector damage behavior).

For example, if you use a SLOT connector, plasticity and damage behavior cannot be specified in the intrinsically constrained 2- and 3-directions. To resolve the issue, you can use a CARTESIAN connector with rigid behavior in components 2 and 3 as discussed above and then define rigid plasticity (and/or damage) in these components. See the examples in Connector plastic behavior for illustrations.

In Abaqus/Standard an overconstraint may occur if a rigid component is defined in the same local direction as an active connector stop, connector lock, or specified connector motion.

CONNECTOR ELASTICITY, RIGID, COMPONENT=n

CONNECTOR ELASTICITY, RIGID
data line listing components to be made rigid

CONNECTOR ELASTICITY, RIGID
(no data lines)

Interaction module: connector section editor: AddElasticity: Definition: Rigid, Components: component or components

Available components of relative motion with connector elasticity use the linearized elastic stiffness from the base state. In direct-solution steady-state dynamic and subspace-based steady-state dynamic analyses, the linear elastic stiffness defined by an uncoupled connector elasticity behavior may be frequency dependent.