Rotation variables | ||||||
|
| |||||
ProductsAbaqus/StandardAbaqus/Explicit
The finite rotation vector, , consists of a rotation magnitude, , and a rotation axis or direction in space, . Physically, the rotation is interpreted as a rotation by radians around the axis . To characterize this finite rotation mathematically, the rotation vector is used to define an orthogonal transformation or rotation matrix. To do so, first define the skew-symmetric matrix associated with by the relationships
is called the axial vector of the skew-symmetric matrix . In matrix components relative to the standard Euclidean basis, if , then
In what follows, will be used to denote the skew-symmetric matrix with axial vector .
A well-known result from linear algebra is that the exponential of a skew-symmetric matrix is an orthogonal (rotation) matrix that produces the finite rotation . Let the rotation matrix be , such that . Then by definition,
However, the above infinite series has the following closed-form expression:
In components,
where and is the alternator tensor, defined by
It is this closed-form expression that allows the exact and numerically efficient geometric representation of finite rotations.
Quaternion parametrization
Even though Abaqus stores and outputs the rotation vector, quaternion parameters prove to be an efficient and convenient way to treat finite rotations computationally. Let be a scalar, and let be a vector field. The quaternion is simply the pairing
To associate with the finite rotation vector , define the following:
By trigonometric identities it follows that the orthogonal matrix in Equation 1 is given in terms of as
By the convention introduced above, is the skew-symmetric matrix with axial vector .
For a more detailed discussion of quaternion algebra and its relation to other representations of finite rotations, see the discussion by Spring (1986).
![]()
Compound rotations
A compound rotation is the successive application of two or more rotation fields. In geometrically linear problems compound rotations are obtained simply as the linear superposition of the individual (linearized) rotation vectors. This fact follows directly from the series expansion for . Let and be infinitesimal rotations. Thus, , , and
In geometrically nonlinear analysis compound rotations are no longer additive. Furthermore, they are not commutative; that is, the order of application is important. A significant exception occurs when the multiple rotations share the same rotation axis. This special case is investigated further below. A detailed example of a finite compound rotation is given in Conventions.
Let be the orthogonal transformation representing the compound rotation defined as the product of a set of individual or incremental rotations , for . (For the case of specified boundary conditions is the final product after i steps of all the specified rotations ; for the iterative numerical solution procedure is the total rotation after i increments, where , for , is the converged rotation field solution at each increment.) By definition, the compound rotation is the product
or equivalently by the recursion relation,
It is important to note that , which is interpreted as the finite rotation superposed on the finite rotation , is different from , which is interpreted as the finite rotation superposed on the finite rotation .
Although compound rotations are defined in terms of orthogonal matrices, in a numerical context the rotation vectors (or equivalently the quaternion parameters) associated with the rotation matrices are the degrees of freedom. Compound rotations are performed as follows: Given a quaternion parametrization and an incremental (finite) rotation , where is defined in terms of an incremental rotation vector by Equation 2, the total or compound rotation is given by the quaternion , which is calculated as
Here denotes the quaternion product and is defined as
Equation 4 allows for the update of rotation fields without ever calculating the orthogonal matrix from the quaternion and without performing a matrix multiplication. Furthermore, all operations are singularity free regardless of the magnitude of the incremental rotation field . The final (total) rotation vector can be calculated from the quaternion by inverting Equation 2.
For the special case when compound rotations share the same rotation axis, the compound rotation reduces to an additive form. Let and have the same rotation axis . Then , , and
which reduces to
![]()
Rotation vector extraction
For output purposes it is necessary to extract the rotation vector corresponding to a given quaternion. The extraction procedure is as follows: Let be the quaternion, and let be the rotation vector. Thus,
It is important to note that the extraction of the rotation vector from the quaternion is not unique. The magnitude is determined only up to the addition of , Abaqus will always choose that rotation vector such that .
![]()
Director and rotation field updates
As an example of the utility of the quaternion parameters, consider the incremental update of a director field for either a beam or shell analysis. At some stage of the solution the director field , the quaternion parametrization of the rotation field , and the incremental rotation field are known at increment i. To update the director field by the incremental rotation to increment , proceed as follows: First calculate the quaternion parametrization of the incremental rotation:
The director field at is then defined as , where is calculated with Equation 3. Thus, the director is calculated directly from the quaternion as
Furthermore, the update of the rotation field is obtained by quaternion multiplication and is defined by
![]()
Variations of the rotation field
In the development of the balance equations, it is necessary to calculate the variation of the rotation field. Consider the vector field , which is obtained by rotation of the reference vector field :
Variations in this field are obtained as
where is the linearized rotation matrix; that is, the variation of the orthogonal tensor . On the other hand, the variation can be defined in terms of the linearized rotation field :
Consequently, it follows that
It is important to note that the linearized rotation , which is analogous to the angular velocity in dynamics, is not the variation of the rotation vector . By a straightforward (but involved) calculation, it can be shown that the variation of the rotation vector () is related to the linearized rotation by
where
The inverse of is
Let represent an infinitesimal change in the rotation field. A direct calculation of the variation of , which is equivalent to calculation of the second variation of either or , leads to an expression that is not symmetric in the variations and the changes . However, it is shown in Simo (1992) that the correct definition of the Hessian operator—that is, the “covariant” derivative of the weak form of the balance equations—requires only the symmetric part (with respect to the variations) of the second variation. Thus, without loss of generality, we can write
Similarly, the second variation of the vector field rotated by can be written as
![]()
Velocity and acceleration
Taking the time derivative of the rotation matrix, we find with the same arguments as used in the calculation of the variations that
where is the angular velocity matrix. Equivalently, the first and second time derivative of are written as
The instantaneous angular velocity vector is related to the time rate of change of the rotation vector by the relation
where is given by Equation 6.
In the linearization of the dynamic balance equations, it is necessary to calculate the variation of the angular velocity, . This quantity, however, can be calculated only by linearizing the specific algorithm used for the time integration of the dynamic equations.
![]()
Coupling of rotations: constant velocity joint
Next, a more rigorous treatment of the two-dimensional constant velocity joint described in MPC is presented. This derivation exemplifies some of the issues associated with the treatment of finite rotations. Uniform collapse of straight and curved pipe segments deals with a different finite rotation constraint and tackles additional complications.
Let a, b, c (see Figure 1) be the nodes making up the joint, with a the dependent node.
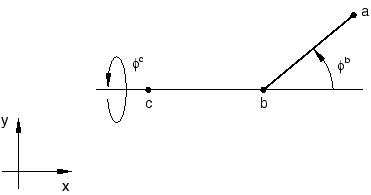
The joint is operated by prescribing an axial rotation at c and an out-of-plane rotation at b. The compounding of these two prescribed rotation fields will determine the total rotation at a. We can formally write this constraint as follows:
The constraint can be written in terms of the rotation matrices as
With the previously defined variational expressions, the constraint can be linearized as
This expression can be simplified by right-multiplying the expression by and by making use of the constraint Equation 7, which yields
which can be written in vector form as
Since
the linearized constraint is indeed identical to the one derived based on simple linear considerations in Linear constraint equations.
The linearized constraint is used for the calculation of equilibrium. It can also be used for the recovery of the dependent rotation, , as is done in Linear constraint equations. The resulting rotation will satisfy the constraint approximately (unless one of the angles or is constant, in which case the constraint is linear and the recovery is exact).
For an exact enforcement of the constraint, user subroutine MPC must define the components of the total rotation vector exactly. To do so, must be updated based on the current values of and . This is most easily accomplished with the aid of the quaternion parameters. Let and be the quaternion parameterizations associated with the finite rotation vectors and , respectively. The total compound rotation is given by the quaternion , where
according to the quaternion compound formula Equation 4. The rotation vector is extracted from the quaternion as follows:
where is the norm of the vector .
MPC shows the implementation of the linearized form of the constraint in user subroutine MPC. The implementation of the exact nonlinear constraint is shown below:
SUBROUTINE MPC(UE,A,JDOF,MDOF,N,JTYPE,X,U,UINIT,MAXDOF,LMPC,
* KSTEP,KINC,TIME,NT,NF,TEMP,FIELD)
C
INCLUDE 'ABA_PARAM.INC'
C
DIMENSION UE(MDOF), A(MDOF,MDOF,N), JDOF(MDOF,N), X(6,N),
* U(MAXDOF,N), UINIT(MAXDOF,N), TIME(2), TEMP(NT,N),
* FIELD(NF,NT,N)
PARAMETER( SMALL = 1.E-14 )
C
IF ( JTYPE .EQ. 1 ) THEN
A(1,1,1) = 1.
A(2,2,1) = 1.
A(3,3,1) = 1.
A(3,1,2) = -1.
A(1,1,3) = -COS(U(6,2))
A(2,1,3) = -SIN(U(6,2))
C
JDOF(1,1) = 4
JDOF(2,1) = 5
JDOF(3,1) = 6
JDOF(1,2) = 6
JDOF(1,3) = 4
C
CPHIB = COS(0.5*U(6,2))
SPHIB = SIN(0.5*U(6,2))
CPHIC = COS(0.5*U(4,3))
SPHIC = SIN(0.5*U(4,3))
C
QA0 = CPHIB*CPHIC
QAX = CPHIB*SPHIC
QAY = SPHIB*SPHIC
QAZ = CPHIB*SPHIC
C
QAMAG = SQRT( QAX*QAX + QAY*QAY + QAZ*QAZ )
IF ( QAMAG .GT. SMALL ) THEN
PHIA = 2.*ATAN2( QAMAG , QA0 )
UE(1) = PHIA*QAX/QAMAG
UE(2) = PHIA*QAY/QAMAG
UE(3) = PHIA*QAZ/QAMAG
ELSE
UE(1) = 0.
UE(2) = 0.
UE(3) = 0.
END IF
END IF
C
RETURN
END