MPC

Coding methods

There are two methods for coding this routine. By default, the subroutine operates in a degree of freedom mode. In this mode each call to this subroutine allows one individual degree of freedom to be constrained. Alternatively, you can specify that the subroutine operate in a nodal mode. In this mode each call to this subroutine allows a set of constraints to be imposed all at once; that is, on multiple degrees of freedom of the dependent node. In either case, the routine will be called for each user-subroutine-defined multi-point constraint or set of constraints. See General multi-point constraints for details.

Constraints that involve rotational degrees of freedom

In geometrically nonlinear analyses Abaqus/Standard compounds three-dimensional rotations based on a finite-rotation formulation and not by simple addition of the individual rotation components (see Conventions and Rotation variables). An incremental rotation involving one component usually results in changes in all three total rotation components. Therefore, any general constraint that involves large three-dimensional rotations should be implemented using the nodal mode of user subroutine MPC. The single degree of freedom version of user subroutine MPC can be used for geometrically linear problems, geometrically nonlinear problems with planar rotations, and constraints that do not involve rotation components.

Constraints that involve degrees of freedom that are not active in the model

The degrees of freedom involved in user MPCs must appear on some element or Abaqus/StandardMPC type in the model: user MPCs cannot use degrees of freedom that have not been introduced somewhere on an element. For example, a mesh that uses only continuum (solid) elements cannot have user MPCs that involve rotational degrees of freedom. The simplest way to overcome this limitation is to introduce an element somewhere in the model that uses the required degrees of freedom but does not affect the solution in any other way. Alternatively, if the degrees of freedom are rotations, they can be activated by the use of a library BEAM-type MPC somewhere in the model.

Use with nodal coordinate systems

When a local coordinate system (Transformed coordinate systems) and a user MPC are both used at a node, the variables at the node are first transformed before the MPC is imposed. Therefore, user-supplied MPCs must be based on the transformed degrees of freedom. The local-to-global transformation matrices $T^{I}$ for the individual nodes:

u_{g l o b a l}^{I} = T^{I} \cdot u_{l o c a l}^{I}

are passed in for information.

Degree of freedom version of user subroutine MPC

This version of user subroutine MPC allows for one individual degree of freedom to be constrained and, thus, eliminated at a time. The constraint can be quite general and nonlinear of the form:

f (u^{1}, u^{2}, u^{3}, \dots, u^{N}, geometry, temperature, field
  variables) = 0.

The first degree of freedom in this function, $u^{1}$ , is the degree of freedom that will be eliminated to impose the constraint. $u^{2}$ , $u^{3}$ , etc. are any other degrees of freedom that are involved in the constraint. Since $u^{1}$ will be eliminated to impose the constraint, it cannot be used in subsequent kinematic constraints (multi-point constraints, linear equation constraints, or boundary conditions). Therefore, the user MPCs are imposed in the order given in the input.

You must provide, at all times, two items of information in user subroutine MPC:

A list of degree of freedom identifiers at the nodes that are listed in the corresponding multi-point constraint definition. This list corresponds to $u^{1}, u^{2}, u^{3}$ , etc. in the constraint as given above.
An array of the derivatives
$A^{1} = \frac{\partial f}{\partial u^{1}}, A^{2} = \frac{\partial f}{\partial u^{2}}, A^{3} = \frac{\partial f}{\partial u^{3}}, \dots$
of the constraint function with respect to the degrees of freedom involved. This array is needed for the redistribution of loads from degree of freedom $u^{1}$ to the other degrees of freedom and for the elimination of $u^{1}$ from the system matrices.
In addition, you can provide the value of the dependent degree of freedom $u^{1}$ as a function of the independent degrees of freedom $u^{2}, u^{3},$ etc. If this value is not provided, Abaqus/Standard will update $u^{1}$ based on the linearized form of the constraint equation as
$u^{1} = - \frac{1}{A^{1}} \overset{N}{\sum_{i = 2}} A^{i} u^{i} .$
Subroutine MPC should be coded and checked with care: if the array of derivatives $\partial f / \partial u^{1}$ , etc. does not correspond to the definition of $u^{1}$ in terms of $u^{2}$ , $u^{3}$ , etc., forces will be transmitted improperly by the MPC and violations of equilibrium may occur. In addition, convergence of the solution may be adversely affected.

User subroutine interface

      SUBROUTINE MPC(UE,A,JDOF,MDOF,N,JTYPE,X,U,UINIT,MAXDOF,
     * LMPC,KSTEP,KINC,TIME,NT,NF,TEMP,FIELD,LTRAN,TRAN)
C
      INCLUDE 'ABA_PARAM.INC'
C
      DIMENSION A(N),JDOF(N),X(6,N),U(MAXDOF,N),UINIT(MAXDOF,N),
     * TIME(2),TEMP(NT,N),FIELD(NF,NT,N),LTRAN(N),TRAN(3,3,N)


      user coding to define UE, A, JDOF, and, optionally, LMPC


      RETURN
      END

Variables to be defined

A(N)

An array containing the derivatives of the constraint function,

A (1) = \frac{\partial f}{\partial u^{1}}, A (2) = \frac{\partial f}{\partial u^{2}}, \dots

The coding in the subroutine must define N entries in A, where N is defined below.

JDOF(N)

An array containing the degree of freedom identifiers at the nodes that are involved in the constraint. For example, if $u^{1}$ is the z-displacement at a node, give JDOF(1) = 3; if $u^{2}$ is the x-displacement at a node, give JDOF(2) = 1. The coding in the subroutine must define N entries in JDOF, where N is defined below.

Variables that can be updated

UE

This variable is passed in as the total value of the eliminated degree of freedom, $u^{1}$ . This variable will either be zero or have the current value of $u^{1}$ based on the linearized constraint equation, depending at which stage of the iteration the user subroutine is called. If the constraint is linear and is used in a small-displacement analysis (nonlinear geometric effects are not considered) or in a perturbation analysis, this variable need not be defined: Abaqus/Standard will compute $u^{1}$ as

u^{1} = - \frac{1}{A^{1}} \overset{N}{\sum_{i = 2}} A^{i} u^{i} .

If the constraint is nonlinear, this variable should be updated to the value of $u^{1}$ at the end of the increment to satisfy the constraint exactly. If the return value is the same as the incoming value, Abaqus/Standard will update the eliminated degree of freedom based on the linearized form of the constraint equation. In this case the constraint is not likely to be satisfied exactly.

LMPC

Set this variable to zero to avoid the application of the multi-point constraint. The MPC will be applied if the variable is not changed. This variable must be set to zero every time the subroutine is called if the user MPC is to remain deactivated. This MPC variable is useful for switching the MPC on and off during an analysis. However, the option should be used with care: switching off an MPC may cause a sudden disturbance in equilibrium, which can lead to convergence problems. If this variable is used to switch on an MPC during an analysis, the variable UE should be defined; otherwise, the constraint may not be satisfied properly.

Variables passed in for information

MDOF: Maximum number of active degrees of freedom per node involved in the MPC. For the degree of freedom mode of user subroutine MPC, MDOF= 1.
N: Number of degrees of freedom that are involved in the constraint, defined as the number of nodes given in the corresponding multi-point constraint definition. If more than one degree of freedom at a node is involved in a constraint, the node must be repeated as needed or, alternatively, the nodal mode should be used.
JTYPE: Constraint identifier given for the corresponding multi-point constraint definition.
X(6,N): An array containing the original coordinates of the nodes involved in the constraint.
U(MAXDOF,N): An array containing the values of the degrees of freedom at the nodes involved in the constraint. These values will be either the values at the end of the previous iteration or the current values based on the linearized constraint equation, depending at which stage of the iteration the user subroutine is called.
UINIT(MAXDOF,N): An array containing the values at the beginning of the current iteration of the degrees of freedom at the nodes involved in the constraint. This information is useful for decision-making purposes when you do not want the outcome of a decision to change during the course of an iteration. For example, there are constraints in which the degree of freedom to be eliminated changes during the course of the analysis, but it is necessary to prevent the choice of the dependent degree of freedom from changing during the course of an iteration.
MAXDOF: Maximum degree of freedom number at any node in the analysis. For example, for a coupled temperature-displacement analysis with continuum elements, MAXDOF will be equal to 11.
KSTEP: Step number.
KINC: Increment number within the step.
TIME(1): Current value of step time.
TIME(2): Current value of total time.
NT: Number of positions through a section where temperature or field variable values are stored at a node. In a mesh containing only continuum elements, NT=1. For a mesh containing shell or beam elements, NT is the largest of the values specified for the number of temperature points in the shell or beam section definition (or 2 for temperatures specified together with gradients for shells or two-dimensional beams, 3 for temperatures specified together with gradients for three-dimensional beams).
NF: Number of different predefined field variables requested for any node (including field variables defined as initial conditions).
TEMP(NT,N): An array containing the temperatures at the nodes involved in the constraint. This array is not used for a heat transfer, coupled temperature-displacement, coupled thermal-electrical, or coupled thermal-electrical-structural analysis since the temperatures are degrees of freedom of the problem.
FIELD(NF,NT,N): An array containing all field variables at the nodes involved in the constraint.
LTRAN(N): An integer array indicating whether the nodes in the MPC are transformed. If LTRAN(I)=1, a transformation is applied to node I; if LTRAN(I)=0, no transformation is applied.
TRAN(3,3,N): An array containing the local-to-global transformation matrices for the nodes used in the MPC. If no transformation is present at node I, TRAN(*,*,I) is the identity matrix.

Example: Nonlinear single degree of freedom MPC

An example of a nonlinear single degree of freedom MPC is a geometrically nonlinear two-dimensional slider involving nodes a, b, and c. The constraint forces node a to be on the straight line connecting nodes b and c (see Figure 1).

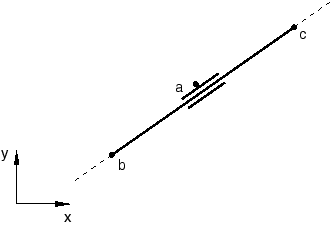
Figure 1. Nonlinear MPC example: two-dimensional slider.

The constraint equation can be written in the form

f (u^{a}, v^{a}, u^{b}, v^{b}, u^{c}, v^{c}) = (x^{a} - x^{b}) (y^{c} - y^{b}) - (y^{a} - y^{b}) (x^{c} - x^{b}) = 0,

where $(x^{a}, y^{a})$ , $(x^{b}, y^{b})$ , and $(x^{c}, y^{c})$ are the current locations of a, b, and c. The derivatives are readily obtained as

\frac{\partial f}{u^{a}} = y^{c} - y^{b}, \frac{\partial f}{u^{b}} = y^{a} - y^{c}, \frac{\partial f}{u^{c}} = y^{b} - y^{a},

\frac{\partial f}{v^{a}} = x^{b} - x^{c}, \frac{\partial f}{v^{b}} = x^{c} - x^{a}, \frac{\partial f}{v^{c}} = x^{a} - x^{b} .

Depending on the orientation of the segment $(b, c),$ we choose either $u^{a}$ or $v^{a}$ as the degree of freedom to be eliminated. If $| x^{c} - x^{b} | \geq | y^{c} - y^{b} |$ , we choose $v^{a}$ as the dependent degree of freedom. If $| x^{c} - x^{b} | < | y^{c} - y^{b} |$ , we choose $u^{a}$ as the dependent degree of freedom. Moreover, if points b and c are coincident, the constraint is not applied.

To prevent the choice of either $u^{a}$ or $v^{a}$ as the dependent degree of freedom from changing during the course of an iteration, the orientation of the segment $(b, c)$ is tested based on the geometry at the beginning of the iteration. The dependent degree of freedom is allowed to change from increment to increment.

Suppose the above multi-point constraint is defined as type 1, with nodes a, a, b, b, c, c. The user subroutine MPC could be coded as follows:

      SUBROUTINE MPC(UE,A,JDOF,MDOF,N,JTYPE,X,U,UINIT,MAXDOF,
     * LMPC,KSTEP,KINC,TIME,NT,NF,TEMP,FIELD,LTRAN,TRAN)
C
      INCLUDE 'ABA_PARAM.INC'
C
      DIMENSION A(N),JDOF(N),X(6,N),U(MAXDOF,N),UINIT(MAXDOF,N),
     * TIME(2),TEMP(NT,N),FIELD(NF,NT,N),LTRAN(N),TRAN(3,3,N)
      PARAMETER( PRECIS = 1.D-15 )
C
      IF (JTYPE .EQ. 1) THEN
        DYBC0 = X(2,5) + UINIT(2,5) - X(2,3) - UINIT(2,3)
        DXBC0 = X(1,3) + UINIT(1,3) - X(1,5) - UINIT(1,5)
        DYBC = X(2,5) + U(2,5) - X(2,3) - U(2,3)
        DXBC = X(1,3) + U(1,3) - X(1,5) - U(1,5)
        A(3) = X(2,1) + U(2,1) - X(2,5) - U(2,5)
        A(4) = X(1,5) + U(1,5) - X(1,1) - U(1,1)
        A(5) = X(2,3) + U(2,3) - X(2,1) - U(2,1)
        A(6) = X(1,1) + U(1,1) - X(1,3) - U(1,3)
        JDOF(3) = 1
        JDOF(4) = 2
        JDOF(5) = 1
        JDOF(6) = 2
        IF (ABS(DYBC0).LE.PRECIS .AND. ABS(DXBC0).LE.PRECIS) THEN
C
C         POINTS B AND C HAVE COLLAPSED. DO NOT APPLY CONSTRAINT.
C
          LMPC = 0
        ELSE IF (ABS(DXBC0) .LT. ABS(DYBC0)) THEN
C
C         MAKE U_A DEPENDENT DOF.
C
          JDOF(1) = 1
          JDOF(2) = 2
          A(1) = DYBC
          A(2) = DXBC
          UE = A(5)A(2)/A(1) + X(1,3) + U(1,3) - X(1,1)
        ELSE
C
C         MAKE V_A DEPENDENT DOF.
C
          JDOF(1) = 2
          JDOF(2) = 1
          A(1) = DXBC
          A(2) = DYBC
          UE = -A(6)A(2)/A(1) + X(2,3) + U(2,3) - X(2,1)
        END IF
      END IF
C
      RETURN
      END

Nodal version of user subroutine MPC

The nodal version of user subroutine MPC allows for multiple degrees of freedom of a node to be eliminated simultaneously. The set of constraints can be quite general and nonlinear, of the form

f_{i} (u^{1}, u^{2}, u^{3}, \dots, u^{N}, geometry, temperature, field
  variables) = 0 i = 1, 2, \dots, NDEP .

NDEP is the number of dependent degrees of freedom that are involved in the constraint and should have a value between 1 and MDOF, which is the number of active degrees of freedom per node in the analysis. N is the number of nodes involved in the constraint. The scalar constraint functions $f_{i}$ can also be considered as a vector function $f$ , and the first set of degrees of freedom $u^{1}$ in the vector function $f$ will be eliminated to impose the constraint. The sets $u^{2}$ , $u^{3}$ , etc. are the independent degrees of freedom at nodes 2, 3, etc. involved in the constraint. The set $u^{1}$ must be composed of NDEP degrees of freedom at the first node of the MPC definition. For example, if the dependent degrees of freedom are the x-displacement, the z-displacement, and the y-rotation at the first node, $u^{1} = (u_{x}^{1}, u_{z}^{1}, ϕ_{y}^{1})$ . $u^{2}$ , $u^{3},$ etc. can be composed of any number of degrees of freedom, depending on which ones play a role in the constraint, and need not be of the same size; for example, $u^{2} = (u_{y}^{2})$ and $u^{3} = (u_{x}^{3}, u_{y}^{3}, u_{z}^{3})$ .

The dependent node can also reappear as an independent node in the MPC. However, since the dependent degrees of freedom of this node will be eliminated, they cannot be used as independent degrees of freedom in this MPC. For example, if the rotations at node a are constrained by the MPC, the displacements of node a can still be used as independent degrees of freedom in the MPC, but the rotations themselves cannot. Similarly, the degrees of freedom that will be eliminated to impose the constraint cannot be used in subsequent kinematic constraints (multi-point constraints, linear equation constraints, or boundary conditions). The MPCs are imposed in the order given in the input for this purpose.

The nodal version of user subroutine MPC was designed with the application of nonlinear constraints involving large three-dimensional rotations in mind. Due to the incremental nature of the solution procedure in Abaqus/Standard, a linearized set of constraints

δ f_{i} = A_{i}^{1} \cdot δ u^{1} + A_{i}^{2} \cdot δ u^{2} + A_{i}^{3} \cdot δ u^{3} + \dots = 0 i = 1, 2, \dots, NDEP,

where $A_{i}^{1} = A_{i}^{1} (u^{1}, u^{2}, \dots)$ , $A_{i}^{2} = A_{i}^{2} (u^{1}, u^{2}, \dots)$ , etc. is applied during each iteration. This linearized set of constraints is used for the calculation of equilibrium. For finite rotations the linearized equation is given in terms of the linearized rotations $δ θ^{1}$ , $δ θ^{2}$ , $δ θ^{3}$ , … , yielding

δ f_{i} = A_{i}^{1} \cdot δ θ^{1} + A_{i}^{2} \cdot δ θ^{2} + A_{i}^{3} \cdot δ θ^{3} + \dots = 0 i = 1, 2, \dots, NDEP .

Since the linearized rotation field, $δ θ$ , is not the variation of the total rotation vector, $ϕ$ (see Rotation variables), you cannot obtain the linearized constraint equation by simply taking derivatives of the vector function, $f$ , with respect to the rotational degrees of freedom involved. The formulation of the linearized constraint in $δ θ$ is equivalent to the formulation of a geometrically linear constraint in the deformed configuration and is generally easier to formulate than the constraint in terms of $δ ϕ$ . For an exact formulation of the constraint, the dependent components of the total rotation vector $ϕ^{1}$ must be defined exactly (see Rotation variables).

You must provide, at all times, two items of information in subroutine MPC:

A matrix of degree of freedom identifiers at the nodes that are listed in the corresponding multi-point constraint definition. The columns of this matrix correspond to $u^{1}, u^{2}, u^{3}$ , etc. in the set of constraints as given above, where unused entries are padded with zeros. The number of nonzero entries in $u^{1}$ will implicitly determine the number of dependent degrees of freedom, NDEP.
The matrices representing the linearized constraint function with respect to the degrees of freedom involved. These matrices are needed for the redistribution of loads from degrees of freedom $u^{1}$ to the other degrees of freedom and for the elimination of $u^{1}$ from the system matrices. For constraints that do not involve three-dimensional rotations and constraints with planar rotations, these matrices can be readily obtained from the derivatives of the total constraint function with respect to the degrees of freedom involved:
$A_{i j}^{1} = \frac{\partial f_{i}}{\partial u_{j}^{1}}, A_{i j}^{2} = \frac{\partial f_{i}}{\partial u_{j}^{2}}, A_{i j}^{3} = \frac{\partial f_{i}}{\partial u_{j}^{3}}, \dots$
For constraints that involve finite rotations, the matrices follow from the linearized form:
$A_{i j}^{1} δ θ_{j}^{1} + A_{i j}^{2} δ θ_{j}^{2} + A_{i j}^{3} δ θ_{j}^{3} + \dots = 0 .$
In addition, you can provide the values of the dependent degrees of freedom $u^{1}$ , as a function of the independent degrees of freedom $u^{2}, u^{3},$ etc. For finite rotations, $ϕ^{1}$ must be specified as a function of $ϕ^{2}$ , $ϕ^{2}$ , etc. If these values are not provided, Abaqus/Standard will update $u^{1}$ based on the linearized form of the constraint equations. Subroutine MPC should be coded and checked with care: if the matrices of derivatives $A_{i j}^{1}$ , etc. do not correspond to the definition of $u^{1}$ in terms of $u^{2}$ , $u^{3},$ etc., forces will be transmitted improperly by the MPC and violations of equilibrium may occur. In addition, convergence of the solution may be adversely affected.

User subroutine interface

      SUBROUTINE MPC(UE,A,JDOF,MDOF,N,JTYPE,X,U,UINIT,MAXDOF,
     * LMPC,KSTEP,KINC,TIME,NT,NF,TEMP,FIELD,LTRAN,TRAN)
C
      INCLUDE 'ABA_PARAM.INC'
C
      DIMENSION UE(MDOF),A(MDOF,MDOF,N),JDOF(MDOF,N),X(6,N),
     * U(MAXDOF,N),UINIT(MAXDOF,N),TIME(2),TEMP(NT,N),
     * FIELD(NF,NT,N),LTRAN(N),TRAN(3,3,N)


      user coding to define JDOF, UE, A and, optionally, LMPC


      RETURN
      END

Variables to be defined

JDOF(MDOF,N)

Matrix of degrees of freedom identifiers at the nodes involved in the constraint. Before each call to MPC, Abaqus/Standard will initialize all of the entries of JDOF to zero. All active degrees of freedom for a given column (first index ranging from 1 to MDOF) must be defined starting at the top of the column with no zeros in between. A zero will mark the end of the list for that column. The number of nonzero entries in the first column will implicitly determine the number of dependent degrees of freedom (NDEP). For example, if the dependent degrees of freedom are the z-displacement, the x-rotation, and the z-rotation at the first node, NDEP $= 3$ and

JDOF (1, 1) = 3, JDOF (2, 1) = 4, JDOF (3, 1) = 6 .

If the degrees of freedom at the third node involved in the MPC are the x-displacement and the y-rotation, define

JDOF (1, 3) = 1, JDOF (2, 3) = 5.

A(MDOF,MDOF,N)

Submatrices of coefficients of the linearized constraint function,

A (I, J, 1) = A_{i j}^{1}, A (I, J, 2) = A_{i j}^{2}, \dots

Before each call to user subroutine MPC, Abaqus/Standard will initialize all of the entries of A to zero; therefore, only nonzero entries need to be defined. If the coding in the subroutine defines NDEP nonzero entries in the column JDOF(J,1), it should define NDEP × NDEP entries in the submatrix A(I,J,1). Since this submatrix will be inverted to impose the MPC, it must be nonsingular. A maximum of NDEP × MDOF entries can be defined for the remaining submatrices A(I,J,K), K = 2, $\dots$ ,N. The number of columns in each submatrix A(I,J,K) must correspond to the number of nonzero entries in the corresponding column of the matrix JDOF(J,K).

Variables that can be updated

UE(NDEP)

This array is passed in as the total value of the eliminated degrees of freedom, $u^{1}$ . This array will either be zero or contain the current values of $u^{1}$ based on the linearized constraint equations, depending at which stage of the iteration the user subroutine is called. For small-displacement analysis or perturbation analysis this array need not be defined: Abaqus/Standard will compute $u^{1}$ as

u_{i}^{1} = - \overset{NDEP}{\sum_{r = 1}} A_{i r}^{1}^{- 1} \overset{N}{\sum_{s = 2}} \overset{MDOF}{\sum_{t = 1}} A_{r t}^{s} u_{JDOF (t, s)}^{s} i = 1, \dots, NDEP .

For large-displacement analysis this array can be updated to the value of $u^{1}$ at the end of the increment to satisfy the constraint exactly. If the return values are the same as the incoming values, Abaqus/Standard will update the eliminated degrees of freedom based on the linearized form of the constraint equations. In this case the constraint is not likely to be satisfied exactly.

LMPC

Set this variable to zero to avoid the application of the multi-point constraint. If the variable is not changed, the MPC will be applied. This variable must be set to zero every time the subroutine is called if the user MPC is to remain deactivated. This MPC variable is useful for switching the MPC on and off during an analysis. This option should be used with care: switching off an MPC may cause a sudden disturbance in equilibrium, which can lead to convergence problems.

Variables passed in for information

MDOF: Number of active degrees of freedom per node in the analysis. For example, for a coupled temperature-displacement analysis with two-dimensional continuum elements, the active degrees of freedom are 1, 2, and 11 and, hence, MDOF will be equal to 3.
N: Number of nodes involved in the constraint. The value of N is defined as the number of nodes given in the corresponding multi-point constraint definition.
JTYPE: Constraint identifier given for the corresponding multi-point constraint definition.
X(6,N): An array containing the original coordinates of the nodes involved in the constraint.
U(MAXDOF,N): An array containing the values of the degrees of freedom at the nodes involved in the constraint. These values will either be the values at the end of the previous iteration or the current values based on the linearized constraint equation, depending at which stage of the iteration the user subroutine is called.
UINIT(MAXDOF,N): An array containing the values at the beginning of the current iteration of the degrees of freedom at the nodes involved in the constraint. This information is useful for decision-making purposes when you do not want the outcome of a decision to change during the course of an iteration. For example, there are constraints in which the degrees of freedom to be eliminated change during the course of the analysis, but it is necessary to prevent the choice of the dependent degrees of freedom from changing during the course of an iteration.
MAXDOF: Maximum degree of freedom number at any node in the analysis. For example, for a coupled temperature-displacement analysis with continuum elements, MAXDOF is equal to 11.
KSTEP: Step number.
KINC: Increment number within the step.
TIME(1): Current value of step time.
TIME(2): Current value of total time.
NT: Number of positions through a section where temperature or field variable values are stored at a node. In a mesh containing only continuum elements, NT=1. For a mesh containing shell or beam elements, NT is the largest of the values specified for the number of temperature points in the shell or beam section definition (or 2 for temperatures specified together with gradients for shells or two-dimensional beams, 3 for temperatures specified together with gradients for three-dimensional beams).
NF: Number of different predefined field variables requested for any node (including field variables defined as initial conditions).
TEMP(NT,N): An array containing the temperatures at the nodes involved in the constraint. This array is not used for a heat transfer, coupled temperature-displacement, coupled thermal-electrical, or coupled thermal-electrical-structural analysis since the temperatures are degrees of freedom of the problem.
FIELD(NF,NT,N): An array containing all field variables at the nodes involved in the constraint.
LTRAN(N): An integer array indicating whether the nodes in the MPC are transformed. If LTRAN(I)=1, a transformation is applied to node I; if LTRAN(I)=0, no transformation is applied.
TRAN(3,3,N): An array containing the local-to-global transformation matrices for the nodes used in the MPC. If no transformation is present at node I, TRAN(*,*,I) is the identity matrix.

Example: Nonlinear MPC

As an example of a nonlinear MPC, consider the insertion of a rigid beam in a large-displacement, planar (two-dimensional) problem. This MPC is the two-dimensional version of library BEAM-type MPC. It can be implemented as a set of three different single degree of freedom MPCs or as a single nodal MPC. Here, the second method will be worked out because it is simpler and requires less data input.

Let a and b (see Figure 2) be the ends of the beam, with a the dependent end.

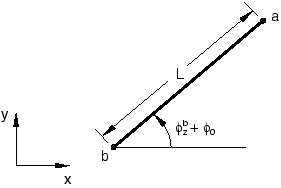
Figure 2. Nonlinear MPC example: rigid beam.

The rigid beam will then define both components of displacement and the rotation at a in terms of the displacements and rotation at end b according to the set of equations:

\begin{matrix} f_{1} (u^{a}, u^{b}) & = x^{a} - x^{b} - L \cos (ϕ_{z}^{b} + ϕ_{0}) = 0, \\ f_{2} (u^{a}, u^{b}) & = y^{a} - y^{b} - L \sin (ϕ_{z}^{b} + ϕ_{0}) = 0, \\ f_{3} (u^{a}, u^{b}) & = ϕ_{z}^{a} - ϕ_{z}^{b} = 0, \end{matrix}

where $u^{a} = (u_{x}^{a}, u_{y}^{a}, ϕ_{z}^{a})$ and $u^{b} = (u_{x}^{b}, u_{y}^{b}, ϕ_{z}^{b})$ , $(x^{a}, y^{a})$ and $(x^{b}, y^{b})$ are the current locations of a and b, $ϕ_{z}^{a}$ and $ϕ_{z}^{b}$ are the rotations at a and b about the z-axis, L is the length of the link, and $ϕ_{0}$ is the original orientation of the link.

In terms of the original positions $(X^{a}, Y^{a})$ and $(X^{b}, Y^{b})$ of a and b,

L = \sqrt{L_{X}^{2} + L_{Y}^{2}}

and

\begin{matrix} \cos ϕ_{0} & = L_{X} / L, \\ \sin ϕ_{0} & = L_{Y} / L, \end{matrix}

where $L_{X} = X^{a} - X^{b}$ and $L_{Y} = Y^{a} - Y^{b}$ . Thus, the constraint equations can be expressed as

\begin{matrix} f_{1} (u^{a}, u^{b}) & = u_{x}^{a} - u_{x}^{b} + L_{X} - L_{X} \cos ϕ_{z}^{b} + L_{Y} \sin ϕ_{z}^{b} = 0, \\ f_{2} (u^{a}, u^{b}) & = u_{y}^{a} - u_{y}^{b} + L_{Y} - L_{X} \sin ϕ_{z}^{b} - L_{Y} \cos ϕ_{z}^{b} = 0, \\ f_{3} (u^{a}, u^{b}) & = ϕ_{z}^{a} - ϕ_{z}^{b} = 0. \end{matrix}

In light of the above formulation, the nontrivial portions of the matrices A and JDOF are

A (1 : 3, 1 : 3, 1) = (\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}), A (1 : 3, 1 : 3, 2) = (\begin{matrix} - 1 & 0 & L_{X} \sin ϕ_{z}^{b} + L_{Y} \cos ϕ_{z}^{b} \\ 0 & - 1 & - L_{X} \cos ϕ_{z}^{b} + L_{Y} \sin ϕ_{z}^{b} \\ 0 & 0 & - 1 \end{matrix})

and

JDOF (1 : 3, 1) = JDOF (1 : 3, 2) = (\begin{matrix} 1 \\ 2 \\ 6 \end{matrix}) .

Since degree of freedom 6 ( $ϕ_{z}$ ) appears in this constraint, there must be an element in the mesh that uses that degree of freedom—a B21 beam element, for example.

If the above multi-point constraint is defined as type 1 with nodes a and b, the user subroutine MPC could be coded as follows:

      SUBROUTINE MPC(UE,A,JDOF,MDOF,N,JTYPE,X,U,UINIT,MAXDOF,LMPC,
     * KSTEP,KINC,TIME,NT,NF,TEMP,FIELD,LTRAN,TRAN)
C
      INCLUDE 'ABA_PARAM.INC'
C
      DIMENSION UE(MDOF),A(MDOF,MDOF,N),JDOF(MDOF,N),X(6,N),
     * U(MAXDOF,N),UINIT(MAXDOF,N),TIME(2),TEMP(NT,N),
     * FIELD(NF,NT,N),LTRAN(N),TRAN(3,3,N)
C
      IF (JTYPE .EQ. 1) THEN
        COSFIB = COS(U(6,2))
        SINFIB = SIN(U(6,2))
        ALX = X(1,1) - X(1,2)
        ALY = X(2,1) - X(2,2)
C
        UE(1) = U(1,2) + ALX*(COSFIB-1.) - ALY*SINFIB 
        UE(2) = U(2,2) + ALY*(COSFIB-1.) + ALX*SINFIB 
        UE(3) = U(6,2)
C
        A(1,1,1) =  1.
        A(2,2,1) =  1.
        A(3,3,1) =  1.
        A(1,1,2) = -1.
        A(1,3,2) =  ALX*SINFIB + ALY*COSFIB
        A(2,2,2) = -1.
        A(2,3,2) = -ALX*COSFIB + ALY*SINFIB
        A(3,3,2) = -1.
C
        JDOF(1,1) = 1
        JDOF(2,1) = 2
        JDOF(3,1) = 6
        JDOF(1,2) = 1
        JDOF(2,2) = 2
        JDOF(3,2) = 6
      END IF
C
      RETURN
      END

Example: Nonlinear MPC involving finite rotations

As an example of a nonlinear MPC involving finite rotations, consider a two-dimensional constant velocity joint that might be part of a robotics application. Let a, b, c (see Figure 3) be the nodes making up the joint, with a the dependent node.

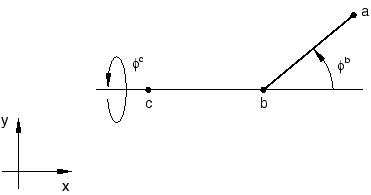
Figure 3. Nonlinear MPC example: constant velocity joint.

The joint is operated by prescribing an axial rotation $ϕ^{c} = ϕ^{c} e_{x}$ at c and an out-of-plane rotation $ϕ^{b} = ϕ^{b} e_{z}$ at b. The compounding of these two prescribed rotation fields will determine the total rotation at a. We can formally write this constraint as follows:

f (ϕ^{a}, ϕ^{b}, ϕ^{c}) = ϕ^{a} - ϕ^{b} \circ ϕ^{c} = 0,

where $\circ$ denotes the rotation product. The formulation of the linearized constraint can be readily achieved from geometrically linear considerations in the deformed state.

In geometrically linear problems compound rotations are obtained simply as the linear superposition of individual rotation vectors. Consider the geometry depicted in Figure 3 and assume that the infinitesimal rotations $δ θ^{c} = δ θ^{c} e_{x}$ and $δ θ^{b} = δ θ^{b} e_{z}$ are applied at c and b, respectively. The rotation $δ θ^{a}$ at a will simply be the sum of the vector $δ θ^{b}$ to the vector $δ θ^{c}$ rotated by an angle $ϕ^{b}$ about the z-axis. Thus, the linearized constraint can be written directly as

\begin{matrix} δ f_{1} (ϕ^{a}, ϕ^{b}, ϕ^{c}) & = δ θ_{x}^{a} - \cos (ϕ^{b}) δ θ^{c} = 0, \\ δ f_{2} (ϕ^{a}, ϕ^{b}, ϕ^{c}) & = δ θ_{y}^{a} - \sin (ϕ^{b}) δ θ^{c} = 0, \\ δ f_{3} (ϕ^{a}, ϕ^{b}, ϕ^{c}) & = δ θ_{z}^{a} - δ θ^{b} = 0. \end{matrix}

In light of this formulation, the nontrivial portions of the matrices JDOF and A are

JDOF (1 : 3, 1) = (\begin{matrix} 4 \\ 5 \\ 6 \end{matrix}), JDOF (1, 2) = 6, JDOF (1, 3) = 4,

and

A (1 : 3, 1 : 3, 1) = (\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}), A (1 : 3, 1, 2) = (\begin{matrix} 0 \\ 0 \\ - 1 \end{matrix}), A (1 : 3, 1, 3) = (\begin{matrix} - \cos (ϕ^{b}) \\ - \sin (ϕ^{b}) \\ 0 \end{matrix}) .

Since degrees of freedom 4 ( $ϕ_{x}$ ), 5( $ϕ_{y}$ ), and 6( $ϕ_{z}$ ) appear in this constraint, there must be an element in the mesh that uses these degrees of freedom—a B31 beam element, for example. The MPC subroutine has been coded with just this information. In this case Abaqus/Standard updates the dependent rotation field, $ϕ^{a}$ , based on the linearized constraint equations. Although the constraint is not satisfied exactly, good results are obtained as long as the rotation increments are kept small enough. A more rigorous derivation of the linearized constraint and the exact nonlinear recovery of the dependent degrees of freedom is presented in Rotation variables.

If the above multi-point constraint is defined as type 1 with nodes a, b, and c, user subroutine MPC could be coded as follows:

      SUBROUTINE MPC(UE,A,JDOF,MDOF,N,JTYPE,X,U,UINIT,MAXDOF,LMPC,
     * KSTEP,KINC,TIME,NT,NF,TEMP,FIELD,LTRAN,TRAN)
C
      INCLUDE 'ABA_PARAM.INC'
C
      DIMENSION UE(MDOF),A(MDOF,MDOF,N),JDOF(MDOF,N),X(6,N),
     * U(MAXDOF,N),UINIT(MAXDOF,N),TIME(2),TEMP(NT,N),
     * FIELD(NF,NT,N),LTRAN(N),TRAN(3,3,N)
C
      IF (JTYPE .EQ. 1) THEN
        A(1,1,1) =  1.
        A(2,2,1) =  1.
        A(3,3,1) =  1.
        A(3,1,2) = -1.
        A(1,1,3) = -COS(U(6,2))
        A(2,1,3) = -SIN(U(6,2))
C
        JDOF(1,1) = 4
        JDOF(2,1) = 5
        JDOF(3,1) = 6
        JDOF(1,2) = 6
        JDOF(1,3) = 4
      END IF
C
      RETURN
     
END