RSURFU

User subroutine to define a rigid surface.

User subroutine RSURFU:

is used to define the surface of a rigid body for use in contact pairs;
can be used to define a complex rigid surface if the various capabilities provided for defining a surface in Abaqus (see Analytical rigid surface definition) are too restrictive;
will be called at points on the slave surface of a contact pair or, if contact elements are used, at each integration point of each contact element with which the rigid surface is associated; and
requires the definition of the closest point on the rigid surface, the normal and tangent directions, and the surface curvature.

The following topics are discussed:

Overpenetration constraint
Calculations to be performed
Defining the local surface geometry
User subroutine interface
Variables to be defined
Variables passed in for information
Example: Rigid punch

Overpenetration constraint

This routine must determine if a point on the slave surface has penetrated the rigid surface and define the local surface geometry. If the deforming and rigid surfaces are in contact at this point, Abaqus/Standard will impose a constraint at the point to prevent overpenetration. The local surface geometry must be defined to provide the necessary orientation for the constraint equations and friction directions and to allow Abaqus/Standard to compute the rate of change of these equations as the point moves around on the surface—the “tangent stiffness matrix” for the surface in the Newton algorithm. For the purpose of these calculations, it is best to define a smooth surface. If the surface is defined in a discontinuous manner, convergence may be adversely affected.

Calculations to be performed

Each time RSURFU is called, Abaqus/Standard gives the current position of point A on the surface of the deforming structure, $x_{A}$ ; the current position of the rigid body reference point, $x_{C}$ ; the total displacements of both of these points, $u_{A}$ and $u_{C}$ ; and the total rotation of the rigid body reference point, $ϕ_{C}$ .

The routine should perform the following calculations:

A point, A′, must be found on the rigid surface at which the normal to the surface passes through $x_{A}$ . If there is not a unique point A′, the routine must choose the most suitable point (usually the closest A′ to A). The routine must pass back the coordinates of A′ to Abaqus/Standard. For the surface-to-surface contact formulation, the slave normal, not the master normal, should be used.
RSURFU must define the distance, h, by which A has penetrated the surface below A′. A negative value of h means that A is outside the surface of the rigid body.
If the surfaces are in contact, which may sometimes be the case even if h is negative, RSURFU must define the local surface geometry.

Defining the local surface geometry

There are two scenarios under which it is mandatory that the routine define the local surface geometry: if A has penetrated the surface— $h > 0$ if the surface behavior is truly rigid, or h is greater than the maximum overclosure value specified for modified surface behavior using either contact controls (see Adjusting contact controls in Abaqus/Standard) or a modified pressure-overclosure relationship (see Contact pressure-overclosure relationships)—and if A was in contact at the beginning of the increment, in which case the flag LCLOSE=1 (see the variable list for the definition of LCLOSE). The variable LCLOSE is not relevant for the surface-to-surface contact formulation and is always passed in as 0. The routine can be coded so that local surface geometry definitions are always provided regardless of the scenario.

The local surface geometry is specified by two orthogonal tangents to the rigid surface at A′, as well as the rates of change of the outward pointing normal at A′, $n$ , with respect to local surface coordinates that are distance measuring along the tangents, $S^{1}$ and $S^{2}$ (see Figure 1).

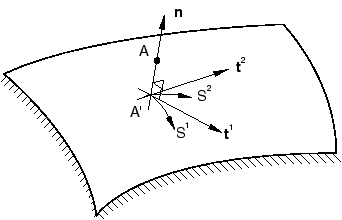
Figure 1. Local geometry on a rigid surface.

The tangents to the surface at A′ must be defined so that their positive, right-handed cross product is the outward normal to the surface. For two-dimensional cases Abaqus/Standard assumes that the second tangent is (0, 0, −1), so that when you give the direction cosines of the first tangent as ( $t_{1}$ , $t_{2}$ , 0), the outward normal will be ( $- t_{2}$ , $t_{1}$ , 0). The rates of change of the normal with respect to $S^{1}$ and $S^{2}$ are required to define the local curvature of the surface.

User subroutine interface

      SUBROUTINE RSURFU(H,P,TGT,DNDS,X,TIME,U,CINAME,SLNAME,
     1 MSNAME,NOEL,NODE,LCLOSE)
C
      INCLUDE 'ABA_PARAM.INC'
C
      CHARACTER*80 CINAME,SLNAME,MSNAME
C
      DIMENSION P(3),TGT(3,2),DNDS(3,2),X(3,3),TIME(2),U(6,2)


      user coding to define H, P, TGT, and DNDS


      RETURN
      END

Variables to be defined

H: Penetration of the point A on the deforming structure into the surface of the rigid body, measured down the outward normal to the rigid surface. A negative value of H indicates that A is outside the rigid surface. Even for a completely rigid surface, A may appear to penetrate the surface during the iterations because the kinematic constraints are not fully satisfied until an increment converges.
P(3): Position of the point A′ on the surface of the rigid body closest to point A on the surface of the deforming structure.
TGT(3,2): Direction cosines of the two unit tangents to the surface, $t^{1}$ and $t^{2}$ , at point A′. For two-dimensional cases only the first two components of $t^{1}$ need be given since in this case Abaqus/Standard assumes that $t^{2}$ is (0, 0, −1).
DNDS(3,2): Rates of change of the surface normal, $n$ , at A′, with respect to distance measuring coordinates, $S^{1}$ and $S^{2}$ , along $t^{1}$ and $t^{2}$ . For two-dimensional cases only the first two entries in the first column of DNDS ( $\partial n_{1} / \partial S^{1}$ , $\partial n_{2} / \partial S^{1}$ ) are required. The array DNDS is not required to be assigned for the surface-to-surface contact formulation.

Variables passed in for information

X(K1,1): Current coordinates of point A on the surface of the deforming structure.
X(K1,2): Current coordinates of the rigid body reference point.
X(K1,3): Unit normal vector for point A; relevant only for the surface-to-surface contact formulation.
TIME(1): Value of step time at the end of the increment.
TIME(2): Value of total time at the end of the increment.
U(K1,1): Total displacement of point A on the surface of the deforming structure.
U(K1,2): Total displacement and rotation of the rigid body reference point; $k_{1} = 1, 2, 3$ are the displacement components, $k_{1} = 4, 5, 6$ are the rotation components. For two-dimensional cases the only nonzero rotation component is $k_{1} = 6$ : U(4,2) and U(5,2) are both zero.
CINAME: User-specified surface interaction name, left justified. For user-defined contact elements it is either the element set name given for the interface definition or the optional name assigned to the interface definition.
SLNAME: Slave surface name. Passed in as blank if RSURFU is called for contact elements.
MSNAME: Master surface name. Passed in as blank if RSURFU is called for contact elements.
NOEL: Element label for contact elements. Passed in as zero if RSURFU is called for a contact pair.
NODE: Node number for point A. For the surface-to-surface contact formulation, this quantity is passed in as 0.
LCLOSE: Flag indicating contact status at the beginning of the increment. LCLOSE=1 indicates that A is in contact (closed) at the beginning of the increment. LCLOSE=0 indicates that A is not in contact (open) at the beginning of the increment. If LCLOSE=1, P, TGT and DNDS must be defined even if A opens during this increment. LCLOSE is not used for the surface-to-surface contact formulation and is passed in as 0.

Example: Rigid punch

The input files for the following examples can be found in RSURFU. The following discussion pertains only to the node-to-surface contact formulation.

Consider the punch shown in Figure 2.

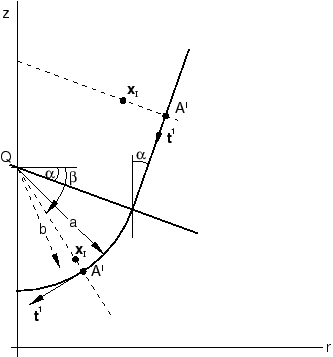
Figure 2. Cross-section of a rigid punch.

It consists of a spherical head of radius a, smoothly merging into a conical section with cone angle $α$ . The center of the sphere lies on the z-axis at Q. We assume that the punch is being driven down the z-axis by a prescribed displacement at the rigid body reference node defined as a boundary condition. (This same surface could be defined directly as a three-dimensional surface of revolution, as described in Analytical rigid surface definition. We define it here in RSURFU as an illustration.)

A point (slave node) on the surface of the deforming body will be associated with the spherical head or with the conical part of the punch, depending on whether it lies above or below the cone that passes through Q and the circle of intersection of the sphere and cone. Thus, define

r = \sqrt{x_{1}^{2} + x_{2}^{2}}, z = x_{3}

in the three-dimensional case or

r = x_{1}, z = x_{2}

in the axisymmetric case. Then, if $r \tan α < z_{Q} - z$ , the point is associated with the spherical surface. Otherwise, it is associated with the cone (both cases are indicated in Figure 2).

Consider first the axisymmetric case. Then, for $r \tan α < z_{Q} - z$ (the sphere) the overclosure is

h = a - b,

where

b = \sqrt{r^{2} + {(z - z_{Q})}^{2}} .

The position of the point A′ on the rigid surface is ( $a \cos β$ , $z_{Q} - a \sin β$ , 0), where

\cos β = r / b, and \sin β = (z_{Q} - z) / b .

The tangent to the rigid surface at A′ is $t^{1} = (- \sin β, - \cos β, 0) .$ The positive direction for $t^{1}$ must be chosen so that the normal satisfies the right-hand rule with respect to $t^{1}$ and $t^{2}$ and points out of the rigid body. Also, $d S^{1} = a d β$ , so that

\frac{\partial n}{\partial S^{1}} = (- \frac{1}{a} \sin β, - \frac{1}{a} \cos β, 0) .

For $r \tan α > z_{Q} - z$ (the conical surface) the clearance is

h = - r \cos α + (z - z_{Q}) \sin α + a,

and the position of the point A′ on the rigid surface is $(r + h \cos α, z - h \sin α) .$ The surface tangent is $t^{1} = (- \sin α, - \cos α, 0)$ and there is no change in $n$ with position, so that

\frac{\partial n}{\partial S^{1}} = (0, 0, 0) .

The routine can then be coded as follows:

      SUBROUTINE RSURFU(H,P,TGT,DNDS,X,TIME,U,CINAME,SLNAME,
     1   MSNAME,NOEL,NODE,LCLOSE)
C     
      INCLUDE 'ABA_PARAM.INC'
C     
      CHARACTER*80 CINAME,SLNAME,MSNAME
      DIMENSION P(3),TGT(3,2),DNDS(3,2),X(3,2),TIME(2),U(6,2)
C     
C     DEFINE THE FOLLOWING QUANTITIES:
C     A = RADIUS 'A' OF THE SPHERICAL HEAD
C     SINA = SINE (CONE ANGLE ALPHA)
C     COSA = COSINE (CONE ANGLE ALPHA)
C     Z0 = ORIGINAL 'Z' COORDINATE OF POINT 'Q'
C     
      A=5.0
      SINA=0.5
      COSA=0.86602
      Z0=6.0
      ZQ=Z0 + U(2,2)
C     
C     TEST FOR SEGMENT
C     
      IF(X(1,1)*SINA/COSA.LT.ZQ-X(2,1))THEN
C     
C     SPHERE
C     
         B=SQRT(X(1,1)**2 + (X(2,1)-ZQ)**2)
         H=A-B
         COSB=X(1,1)/B
         SINB=(ZQ-X(2,1))/B
         P(1)=A*COSB
         P(2)=ZQ-A*SINB
         TGT(1,1)=-SINB
         TGT(2,1)=-COSB
         DNDS(1,1)=-SINB/A
         DNDS(2,1)=-COSB/A
      ELSE
C     CONE
         H=-X(1,1)*COSA+(X(2,1)-ZQ)*SINA+A
         P(1)=X(1,1) + H*COSA
         P(2)=X(2,1)- H*SINA
         TGT(1,1)=-SINA
         TGT(2,1)=-COSA
         DNDS(1,1)=0.
         DNDS(2,1)=0.
      END IF
      RETURN
      END

The above case can be directly extended to three dimensions. For this purpose we assume that the radial axis, r, is in the global (x–y) plane, so that

r = \sqrt{x_{1}^{2} + x_{2}^{2}}, z = x_{3} .

For $r \tan α < z_{Q} - z$ (the sphere), the overclosure is $h = a - b$ , where again

b = \sqrt{r^{2} + {(z - z_{Q})}^{2}} .

The point A′ on the rigid surface is ( $a \cos β \cos γ$ , $a \cos β \sin γ$ , $z_{Q} - a \sin β$ ), where

\cos γ = \frac{x_{1}}{r}, \sin γ = \frac{x_{2}}{r} .

For $r = 0$ , $γ$ is not defined uniquely; in that case we arbitrarily choose $γ = 0$ . We now need two tangents to the surface. The tangent $t^{1}$ used in the axisymmetric case is now

t^{1} = (- \sin β \cos γ, - \sin β \sin γ, - \cos β)

and the orthogonal tangent is

t^{2} = (- \sin γ, \cos γ, 0) .

Again, the positive directions of $t^{1}$ and $t^{2}$ are chosen so that $t^{1} \times t^{2}$ defines an outward normal to the surface. The distance measures on the surface are

d S^{1} = a d β, d S^{2} = a \cos β d γ

so that

\begin{matrix} \frac{\partial n}{\partial S^{1}} = & (- \frac{1}{a} \sin β \cos γ, - \frac{1}{a} \sin β \sin γ, - \frac{1}{a} \cos β), \\ \frac{\partial n}{\partial S^{2}} = & (- \frac{1}{a} \sin γ, \frac{1}{a} \cos γ, 0) . \end{matrix}

For the conical surface ( $r \tan α \geq z_{Q} - z$ ), the surface separation is

h = - r \cos α + (z - z_{Q}) \sin α + a .

The point A′ on the rigid surface is $((r + h \cos α) \cos γ, (r + h \cos α) \sin γ, z - h \sin α);$ and the surface tangents are

\begin{matrix} t^{1} & = (- \sin α \cos γ, - \sin α \sin γ, - \cos α) \\ t^{2} & = (- \sin γ, \cos γ, 0) . \end{matrix}

There is no change of $n$ with respect to $S^{1}$ , and, in this case $d S^{2} = c d γ$ , where $c = r + h \cos α$ so that

\frac{\partial n}{\partial S^{2}} = (- \frac{1}{c} \cos α \sin γ, + \frac{1}{c} \cos α \cos γ, 0) .

The routine can then be coded as follows:

      SUBROUTINE RSURFU(H,P,TGT,DNDS,X,TIME,U,CINAME,SLNAME,
     1     MSNAME,NOEL,NODE,LCLOSE)
C     
      INCLUDE 'ABA_PARAM.INC'
C     
      CHARACTER*80 CINAME,SLNAME,MSNAME
      DIMENSION P(3), TGT(3,2),DNDS(3,2), X(3,2), TIME(2), U(6,2)
C     
C     DEFINE THE FOLLOWING QUANTITIES:
C     A = RADIUS 'A' OF THE SPHERICAL HEAD
C     SINA = SINE (CONE ANGLE ALPHA)
C     COSA = COSINE (CONE ANGLE ALPHA)
C     Z0 = ORIGINAL 'Z' COORDINATE OF POINT 'Q'
C     
      A=5.0
      SINA=0.5
      COSA=0.86603
      Z0=5.0
      ZQ= Z0 + U(3,2)
C     
C     TEST FOR SEGMENT
C     
      R  = SQRT(X(1,1)*X(1,1)+X(2,1)*X(2,1))
      IF(R .GT. 0.0) THEN
         COSG = X(1,1)/R
         SING = X(2,1)/R
      ELSE 
         COSG = 1.0
         SING = 0.0
      END IF
      IF(R*SINA/COSA .LT. ZQ -X(3,1)) THEN
C     
C     SPHERE
C     
         B=SQRT(R*R+(X(3,1)-ZQ)**2)
         H=A-B
         COSB=R/B
         SINB=(ZQ-X(3,1))/B
         P(1)=A*COSB*COSG
         P(2)=A*COSB*SING
         P(3)=ZQ-A*SINB
         TGT(1,1)=-SINB*COSG
         TGT(2,1)=-SINB*SING
         TGT(3,1)=-COSB
         TGT(1,2)=-SING
         TGT(2,2)=COSG
         TGT(3,2)=0.0
         DNDS(1,1)=-SINB*COSG/A
         DNDS(2,1)=-SINB*SING/A
         DNDS(3,1)=-COSB/A
         DNDS(1,2)=-SING/A
         DNDS(2,2)=COSG/A
         DNDS(3,2)=0.0
      ELSE
C     
C     CONE
C     
         H=-R*COSA+(X(3,1)-ZQ)*SINA+A
         P(1)=(R+H*COSA)*COSG
         P(2)=(R+H*COSA)*SING
         P(3)=X(3,1)-H*SINA
         TGT(1,1)=-SINA*COSG
         TGT(2,1)=-SINA*SING
         TGT(3,1)=-COSA
         TGT(1,2)=-SING
         TGT(2,2)=COSG
         TGT(3,2)=0.0
         DNDS(1,1)=0.0
         DNDS(2,1)=0.0
         DNDS(3,1)=0.0
         C=R+H*COSA
         DNDS(1,2)=-COSA*SING/C
         DNDS(2,2)=COSA*COSG/C
         DNDS(3,2)=0.0
      END IF
C     
      RETURN
      END