Adjusting contact controls in Abaqus/Standard | ||
| ||
ProductsAbaqus/StandardAbaqus/CAE
Applying contact controls
You can apply contact controls on a step-by-step basis to all of the contact pairs and contact elements that are active in the step or to individual contact pairs. This makes it possible to apply contact controls to a specific contact pair to take the simulation through a difficult phase. Contact controls remain in effect until they are either changed or reset to their default values. If in any given step the contact controls are declared for both the entire model and for a specific contact pair, the controls for the specific contact pair will override those for the entire model for that contact pair.
In addition, you can specify supplementary contact constraints on individual contact pairs as described below in Supplementary contact constraints.
Input File Usage
To apply contact controls to all contact pairs and contact elements:
CONTACT CONTROLS contact control options
To apply contact controls to a specific contact pair:
CONTACT CONTROLS, SLAVE=slave surface, MASTER=master surface contact control options
Repeat this option to apply contact controls to several contact pairs.
Abaqus/CAE Usage
Contact controls in Abaqus/CAE can be applied only to specific contact pairs:
Interaction module: : Abaqus/Standard contact controls Contact interaction editor: Contact controls: contact controls name
Resetting contact controls
You can reset all contact controls to their default values, or you can reset the controls for a specific contact pair.
Input File Usage
To reset all contact controls:
CONTACT CONTROLS, RESET
To reset the controls for a specific contact pair:
CONTACT CONTROLS, SLAVE=slave surface, MASTER=master surface, RESET
Abaqus/CAE Usage
Interaction module: contact interaction editor: Contact controls: (Default)You cannot reset all contact controls at once in Abaqus/CAE.
![]()
Automatic stabilization of rigid body motions in contact problems
Abaqus/Standard offers contact stabilization to help automatically control rigid body motion in static problems before contact closure and friction restrain such motion.
It is recommended that you first try to stabilize rigid body motion through modeling techniques (modifying geometry, imposing boundary conditions, etc.). The automatic stabilization capability is meant to be used in cases in which it is clear that contact will be established, but the exact positioning of multiple bodies is difficult during modeling. It is not meant to simulate general rigid body dynamics; nor is it meant for contact chattering situations or to resolve initially tight clearances between mating surfaces.
When automatic contact stabilization is used, Abaqus/Standard activates viscous damping for relative motions of the contact pair at all slave nodes, in the same manner as contact damping (see Contact damping). Unlike most contact controls, which carry over to subsequent steps until they are modified or reset, automatic stabilization damping is applied only for the duration of the step in which it is specified. In subsequent steps the stabilization is removed, even if contact was not established or if rigid body motions appear later because of complete separation of the contact pair. If needed, you should specify stabilization for subsequent steps as well.
By default, the damping coefficient:
-
is calculated automatically for each contact constraint based on the stiffness of the underlying elements and the step time,
-
is applied to all contact pairs equally in the normal and tangential directions,
-
is ramped down linearly over the step,
-
is active only when the distance between the contact surfaces is smaller than a characteristic surface dimension, and
-
is zero for contact modeled with contact elements (such as gap contact elements, tube-to-tube contact elements, etc.).
Although the automatically calculated damping coefficient typically provides enough damping to eliminate the rigid body modes without having a major effect on the solution, there is no guarantee that the value is optimal or even suitable. This is particularly true for thin shell models, in which the damping may be too high. Hence, you may have to increase the damping if the convergence behavior is problematic or decrease the damping if it distorts the solution. The first case is obvious, but the latter case requires a postanalysis check. There are several ways to carry out such checks. The simplest method is to consider the ratio between the energy dissipated by viscous damping and a more general energy measure for the model, such as the elastic strain energy. These quantities can be obtained as output variables ALLSD and ALLSE, respectively. More detailed information can be obtained by comparing the contact damping stresses CDSTRESS (with the individual components CDPRESS, CDSHEAR1, and CDSHEAR2) to the true contact stresses CSTRESS (with the individual components CPRESS, CSHEAR1, and CSHEAR2). If the contact damping stresses are too high, you should decrease the damping. The comparison should be made after contact is firmly established; the contact damping stresses will always be relatively high when contact is not yet or only partially established.
The easiest way to increase or decrease the amount of damping is to specify a factor by which the automatically calculated damping coefficient will be multiplied. Typically, you should initially consider changing the default damping by (at least) an order of magnitude; if that addresses the problem sufficiently, you can do some subsequent fine-tuning. In some cases a larger or smaller factor may be needed; this is not a problem as long as a converged solution is obtained and the dissipated energy and contact damping stresses are sufficiently small.
It is also possible to specify the damping coefficient directly. Direct specification of the damping value is not easy and may require some trial and error. For efficiency reasons this may best be done on a similar model of reduced size. If the damping coefficient is specified directly, any multiplication factor specified for the default damping coefficient is ignored.
Input File Usage
To use the default damping coefficient:
CONTACT CONTROLS, STABILIZE
To specify a scale factor for the default damping coefficient:
CONTACT CONTROLS, STABILIZE=factor
To specify the damping coefficient directly:
CONTACT CONTROLS, STABILIZE damping coefficient
Abaqus/CAE Usage
Interaction module: Abaqus/Standard contact controls editor: Stabilization: Automatic stabilization, Factor: factor or Stabilization coefficient: damping coefficient
Changing the stabilization within increments
To reduce or eliminate the likelihood of contact stabilization significantly influencing the reported solution, scale factors can be introduced that vary across iterations of an increment. Having more stabilization in effect during the early iterations of an increment can be helpful to avoid numerical problems prior to establishing some contact. Having less or no stabilization in effect during the later iterations can be helpful to improve the accuracy of the final converged iteration of an increment.
You can specify these scale factors. For example, specifying “1,0” results in the scale factor being unity during initial iterations (until various convergence measures are satisfied or nearly satisfied) and then the scale factor being reset to zero (effectively turning off stabilization) for the final iterations until convergence checks are again satisfied.
Input File Usage
To change the damping coefficients within an increment:
CONTACT CONTROLS, STABILIZE=USER ADAPTIVE
Specifying the stabilization ramp-down factor
You can specify the ramp-down factor at the end of the step. By default, this value is equal to zero, so that the damping vanishes completely at the end of the step. Entering a nonzero value for this factor can be useful in cases where the rigid body modes are not fully constrained at the end of the step; for example, if the problem is frictionless and sliding motions can occur but there is no net force in the sliding direction. In that case it is usually desirable to maintain the small damping in the next step by using the value used for the ramp-down as the multiplication factor for the damping coefficient. If needed, you can maintain this damping level by setting the ramp-down factor equal to one.
Input File Usage
CONTACT CONTROLS, STABILIZE , ramp-down factor
Abaqus/CAE Usage
Interaction module: Abaqus/Standard contact controls editor: Stabilization: Automatic stabilization or Stabilization coefficient, Fraction of damping at end of step: ramp-down factor
Specifying the damping range
By default, the opening distance over which the damping is applied (the damping range) is equal to the characteristic slave surface facet dimension; if such a dimension is not available (for example, in the case of a node-based surface), a characteristic element length obtained for the whole model is used. The damping is 100% of the reference value for openings less than half the damping range and from there is ramped to zero for an opening equal to the damping range. Alternatively, you can specify the damping range directly, overriding the calculated value. This can be useful if the damping should work only for a narrow gap, or if the damping should be in effect regardless of the opening distance. In the latter case a large value should be entered.
Input File Usage
CONTACT CONTROLS, STABILIZE , , damping range
Abaqus/CAE Usage
Interaction module: Abaqus/Standard contact controls editor: Stabilization: Automatic stabilization or Stabilization coefficient, Clearance at which damping becomes zero: Specify: damping range
Specifying tangential damping
By default, the damping in the tangential direction is the same as the damping in the normal direction. However, if a lower or higher value is desired, you can decrease or increase the tangential damping or set it to zero.
Input File Usage
CONTACT CONTROLS, STABILIZE, TANGENT FRACTION=value
Abaqus/CAE Usage
Interaction module: Abaqus/Standard contact controls editor: Stabilization: Automatic stabilization or Stabilization coefficient, Tangent fraction: value
![]()
Contact controls associated with normal contact constraints
These controls allow you to specify that nodes on the contact interfaces can violate “hard” contact conditions. In addition, these controls can be used to modify the behavior of the “softened” pressure-overclosure relationships and the augmented Lagrangian or penalty contact constraint enforcement. The no separation pressure-overclosure relationships cannot be modified by the contact controls.
A node can violate the contact condition in one of two ways. First, Abaqus/Standard may consider that there is no contact at that node, even though the node has penetrated the master surface by a small distance. Second, Abaqus/Standard may consider that there is contact at a node, even though the normal pressure transmitted between the contacting surfaces at the node is negative (that is, a tensile stress is being transmitted).
Modifying the behavior of the augmented Lagrangian or penalty contact constraint enforcement
For augmented Lagrangian contact you can specify the allowable penetration (either directly or as a fraction of a characteristic contact surface dimension) that is permitted to violate the impenetrability condition. In addition, for augmented Lagrangian or penalty contact you can scale the default penalty stiffness calculated by Abaqus/Standard. Controls for the augmented Lagrange and penalty constraint enforcement methods are discussed in Contact constraint enforcement methods in Abaqus/Standard.
![]()
Modifying the tangential penalty stiffness in linear perturbation steps
The penalty stiffness used to enforce tangential constraints in linear perturbation steps generally differs from the penalty stiffness used to enforce sticking in a general step. In perturbation steps Abaqus/Standard activates the tangential contact constraints when the corresponding normal constraint is active in the base state and the contact property (surface interaction) definition includes a friction model. By default, the tangential penalty stiffness is equal to the default normal penalty stiffness.
You can scale the tangential penalty stiffness to simulate sticking/slipping conditions on a step-by-step basis. This scaling only affects the perturbation step in which it is specified; it will not carry over to subsequent steps. If you want the same scale factor applied in a series of perturbation steps, you must specify the scale factor explicitly in each step.
Some procedures that rely on a frequency analysis, such as complex frequency analysis and subspace-based steady-state dynamic analysis, are influenced by the scaling of the tangential stiffness that was in effect for the prior frequency analysis and the scaling of the tangential stiffness that is in effect for these steps. In such cases consistent scaling is recommended for these steps. For other mode-based procedures based on a frequency analysis, the scaling of the tangential stiffness is ignored and only the effect of the previous frequency analysis is considered.
Input File Usage
To modify the tangential penalty stiffness for all contact pairs in a linear perturbation step:
CONTACT CONTROLS, PERTURBATION TANGENT SCALE FACTOR=factor
To modify the tangential penalty stiffness for a specific contact pair in a linear perturbation step:
CONTACT CONTROLS, PERTURBATION TANGENT SCALE FACTOR=factor, SLAVE=slave surface, MASTER=master surface
Abaqus/CAE Usage
Modifying the tangential penalty stiffness in linear perturbation steps is not supported in Abaqus/CAE.
![]()
Contact pressure–dependent constraint enforcement in linear perturbation steps
Except for the LCD perturbation procedure, contact constraints are usually fully enforced during perturbation steps for all closed contact interfaces independent of local normal pressure in the base state. You can use two control pressure coefficients, and , to relax the constraints that have low pressure in the base state or even completely remove them. Both normal and tangential constraints are affected. For pressures less than in the base state, the normal and tangential constraints are effectively removed by setting the constraint stiffness to zero. For pressures greater than , the constraints are enforced fully. For pressures between and , the constraint stiffness is reduced and ramps up linearly between and . In this pressure range finite contact stiffness is in effect even for contact constraints that would otherwise use strict Lagrangian multiplier enforcement. The initial stress stiffness terms are scaled as well.
All other controls for normal and tangential contact penalties are applicable. Constraints open in the base state are unaffected. Pressure-dependent constraint enforcement cannot be used during general steps.
You can specify the contact pressure–dependent constraint enforcement on a step-by-step basis. This specification affects the perturbation step in which it is specified; it will not carry over to subsequent steps. If you want the same specification applied in a series of perturbation steps, you must specify it explicitly in each step.
Some procedures that rely on a frequency analysis, such as complex frequency analysis and subspace-based steady-state dynamic analysis, are influenced by the specification that was in effect for the prior frequency analysis and the specification that is in effect for these steps. In such cases consistent specification is recommended for these steps. For other mode-based procedures based on a frequency analysis, the specification is ignored and only the effect of the previous frequency analysis is considered.
Pressure-dependent constraint enforcement is not available for the static LCP perturbation procedure (Linear Complementarity Problem (LCP) solution technique for solving contact problems).
Input File Usage
To specify base-state pressure-dependent constraint enforcement for all contact pairs in a linear perturbation step:
CONTACT CONTROLS, PRESSURE DEPENDENT PERTURBATION=
To specify base-state pressure-dependent constraint enforcement for a specific contact pair in a linear perturbation step:
CONTACT CONTROLS, PRESSURE DEPENDENT PERTURBATION=, SLAVE=slave surface, MASTER=master surface
Abaqus/CAE Usage
Base-state pressure-dependent constraint enforcement in linear perturbation steps is not supported in Abaqus/CAE.
![]()
Contact controls associated with second-order faces
Second-order elements not only provide higher accuracy but also capture stress concentrations more effectively and are better for modeling geometric features than first-order elements. Surfaces based on second-order element types work well with the surface-to-surface contact formulation but, in some cases, do not work well with the node-to-surface formulation (see Contact formulations in Abaqus/Standard for a discussion of these contact formulations).
Some second-order element types are not well-suited for underlying the slave surface with the combination of a node-to-surface contact formulation and strict enforcement of “hard” contact conditions because of the distribution of equivalent nodal forces when a pressure acts on the face of the element. As shown in Figure 1, a constant pressure applied to the face of a second-order element without a midface node produces forces at the corner nodes acting in the opposite sense of the pressure.
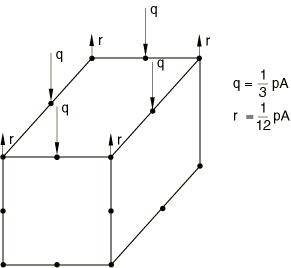
This ambiguous nature of the nodal forces in second-order elements can cause Abaqus/Standard to alter its internal contact logic inadequately. Slave surfaces based on second-order tetrahedral elements can also be problematic for the node-to-surface contact formulation because the distribution of equivalent nodal forces for a pressure acting on a face of these elements is such that the corner nodes have zero force.
Options available in Abaqus/Standard to make it easier to use node-to-surface contact pairs involving second-order slave faces are discussed below. You can also avoid potential difficulties by using the surface-to-surface contact formulation, which is generally preferable.
Manually or automatically adjusting element types
Modified 10-node tetrahedral elements (C3D10M, etc.) do not cause fundamental difficulties for the node-to-surface contact formulation and often provide a viable alternative to 10-node second-order tetrahedral elements (C3D10, C3D10HS, etc.) for models with node-to-surface contact pairs. Trade-offs in characteristics of modified 10-node tetrahedral elements versus second-order tetrahedral elements are discussed in Modified triangular and tetrahedral elements. If desired, you must make this adjustment to the element type as it does not occur automatically.
Abaqus/Standard automatically adds midface nodes to underlying (serendipity) elements of most 8-node slave facets associated with non-tied node-to-surface contact pairs. For the three-dimensional 18-node gasket elements, the midface nodes are also generated automatically if they are not given in the element connectivity. The presence of the midface node results in a distribution of nodal forces that is not ambiguous for the contact algorithm. The element families C3D20(RH), C3D15(H), S8R5, and M3D8 are converted to the families C3D27(RH), C3D15V(H), S9R5, and M3D9, respectively. Since Abaqus/Standard does not convert second-order coupled temperature-displacement, coupled thermal-electrical-structural, and coupled pore pressure–displacement elements, you should use an alternative method to avoid problems with serendipity elements in the node-to-surface contact formulation in those cases. Abaqus/Standard will interpolate nodal quantities, such as temperature and field variables, at the automatically generated midface nodes when values are prescribed at any of the user-defined nodes. Abaqus/Standard does not convert second-order serendipity elements if the slave surface is used in a tied contact pair.
By default, Abaqus/Standard does not automatically add midface nodes to second-order serendipity elements that form a slave surface for surface-to-surface contact pairs; however, an option is available to enable the same algorithm for automatically adding midface nodes as used by node-to-surface contact pairs.
Input File Usage
CONTACT PAIR, TYPE=SURFACE TO SURFACE, MIDFACE NODES=YES
Abaqus/CAE Usage
You cannot enable automatic conversion of serendipity elements underlying slave surfaces of surface-to-surface contact pairs in Abaqus/CAE.
Supplementary contact constraints
Another approach to avoiding difficulties that certain element types present to the node-to-surface contact formulation is to add supplementary contact constraints without changing the underlying element formulation. This approach is applicable only to cases in which node-to-surface contact pairs use penalty or augmented Lagrange constraint enforcement or a softened pressure-overclosure relationship, because it would result in overconstrained conditions if strictly enforced “hard” contact conditions are in effect. Supplementary contact constraints are sometimes helpful for improving convergence behavior or for improving the smoothness and accuracy of the contact pressure and underlying element stress; however, the extra constraints present some risk of degrading convergence behavior. Supplementary constraints are used selectively by default for node-to-surface contact pairs with 6-node slave faces of non-modified elements and 8-node slave faces unless strictly enforced “hard” contact conditions are in effect. You can deactivate supplementary constraints or add activate supplementary constraints for additional second-order element types underlying the slave surface.
Input File Usage
CONTACT PAIR, INTERACTION=interaction_property_name, SUPPLEMENTARY CONSTRAINTS=SELECTIVE slave_surface_name, master_surface_name
Use the following option to add supplementary contact constraints for additional second-order element types:
CONTACT PAIR, INTERACTION=interaction_property_name, SUPPLEMENTARY CONSTRAINTS=YES slave_surface_name, master_surface_name
Use the following option to forgo supplementary contact constraints:
CONTACT PAIR, INTERACTION=interaction_property_name, SUPPLEMENTARY CONSTRAINTS=NO slave_surface_name, master_surface_name
Abaqus/CAE Usage
For a node-to-surface contact formulation:
Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the master surface; click Surface; select the slave surface; Interaction editor; Use supplementary contact points: Selectively, Always, or Never; Contact interaction property: interaction_property_name
![]()
Smoothness of contact force redistribution upon sliding for surface-to-surface contact pairs
You can control the smoothness of nodal contact force redistribution upon sliding for surface-to-surface contact pairs. The default setting, which is generally appropriate, results in the smoothness of the nodal force redistribution being of the same order as the elements underlying the slave surface; that is, linear redistribution smoothness for linear elements, and quadratic redistribution smoothness for second-order elements. Quadratic redistribution smoothness usually tends to improve convergence behavior and improve resolution of contact stresses within regions of rapidly varying contact stresses. However, quadratic redistribution smoothness tends to increase the number of nodes involved in each constraint, which can increase the computational cost of the equation solver. Linear redistribution smoothness tends to provide better resolution of contact stresses near edges of active contact regions and, therefore, occasionally results in better convergence behavior.
Input File Usage
Use the following option to indicate that the smoothness of the contact force redistribution upon sliding should be of the same order as the elements underlying the slave surface for surface-to-surface contact pairs:
CONTACT PAIR, TYPE=SURFACE TO SURFACE, SLIDING TRANSITION=ELEMENT ORDER SMOOTHING slave_surface_name, master_surface_name
Use the following option to indicate linear smoothness of the contact force redistribution upon sliding for surface-to-surface contact pairs:
CONTACT PAIR, TYPE=SURFACE TO SURFACE, SLIDING TRANSITION=LINEAR SMOOTHING slave_surface_name, master_surface_name
Use the following option to indicate quadratic smoothness of the contact force redistribution upon sliding for surface-to-surface contact pairs:
CONTACT PAIR, TYPE=SURFACE TO SURFACE, SLIDING TRANSITION=QUADRATIC SMOOTHING slave_surface_name, master_surface_name
Abaqus/CAE Usage
You cannot change the default contact force redistribution in Abaqus/CAE.