Solving nonlinear problems

The solution of nonlinear problems

The nonlinear load-displacement curve for a structure is shown in Figure 1.

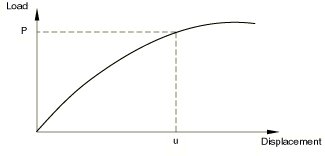
Figure 1. Nonlinear load-displacement curve.

The objective of the analysis is to determine this response. In a nonlinear analysis the solution cannot be calculated by solving a single system of linear equations, as would be done in a linear problem. Instead, the solution is found by specifying the loading as a function of time and incrementing time to obtain the nonlinear response. Therefore, Abaqus/Standard breaks the simulation into a number of time increments and finds the approximate equilibrium configuration at the end of each time increment. Using the Newton method, it often takes Abaqus/Standard several iterations to determine an acceptable solution to each time increment.

Steps, increments, and iterations

The time history for a simulation consists of one or more steps. You define the steps, which generally consist of an analysis procedure, loading, and output requests. Different loads, boundary conditions, analysis procedures, and output requests can be used in each step. For example:

Step 1: Hold a plate between rigid jaws.

Step 2: Add loads to deform the plate.

Step 3: Find the natural frequencies of the deformed plate.
An increment is part of a step. In nonlinear analyses each step is broken into increments so that the nonlinear solution path can be followed. You suggest the size of the first increment, and Abaqus/Standard automatically chooses the size of the subsequent increments. At the end of each increment the structure is in (approximate) equilibrium and results are available for writing to the restart, data, results, or output database files.
An iteration is an attempt at finding an equilibrium solution in an increment. If the model is not in equilibrium at the end of the iteration, Abaqus/Standard tries another iteration. With every iteration the solution that Abaqus/Standard obtains should be closer to equilibrium; however, sometimes the iteration process may diverge—subsequent iterations may move away from the equilibrium state. In that case Abaqus/Standard may terminate the iteration process and attempt to find a solution with a smaller increment size.

Convergence

Consider the external forces, P, and the internal (nodal) forces, I, acting on a body (see Figure 2(a) and Figure 2(b), respectively). The internal loads acting on a node are caused by the stresses in the elements that are attached to that node.

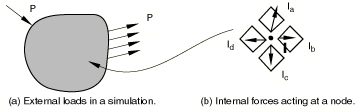
Figure 2. Internal and external loads on a body.

For the body to be in equilibrium, the net force acting at every node must be zero. Therefore, the basic statement of equilibrium is that the internal forces, I, and the external forces, P, must balance each other:

P - I = 0.

The nonlinear response of a structure to a small load increment, $Δ P$ , is shown in Figure 3. According to the Newton method, Abaqus/Standard uses the structure's tangent stiffness, $K_{0}$ , calculated from its configuration at $u_{0}$ , and $Δ P$ to calculate a displacement correction, $c_{a}$ , for the structure. Using $c_{a}$ , the structure's configuration is updated to $u_{a}$ .

Figure 3. First iteration in an increment.

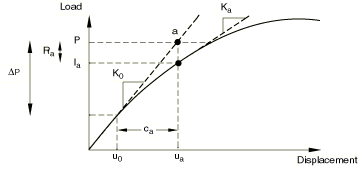
Abaqus/Standard then calculates the structure's internal forces, $I_{a}$ , in this updated configuration. The difference between the total applied load, P, and $I_{a}$ can now be calculated as

R_{a} = P - I_{a},

where $R_{a}$ is the force residual for the iteration.

If $R_{a}$ is zero at every degree of freedom in the model, point a in Figure 3 would lie on the load-deflection curve and the structure would be in equilibrium. In a nonlinear problem $R_{a}$ will never be exactly zero, so Abaqus/Standard compares it to a tolerance value. If $R_{a}$ is less than this force residual tolerance at all nodes, Abaqus/Standard accepts the solution as being in equilibrium. By default, this tolerance value is set to 0.5% of an average force in the structure, averaged over time. Abaqus/Standard automatically calculates this spatially and time-averaged force throughout the simulation. You can change this, and all other such tolerances, by specifying solution controls (see Convergence criteria for nonlinear problems).

If $R_{a}$ is less than the current tolerance value, P and $I_{a}$ are considered to be in equilibrium and $u_{a}$ is a valid equilibrium configuration for the structure under the applied load. However, before Abaqus/Standard accepts the solution, it also checks that the last displacement correction, $c_{a}$ , is small relative to the total incremental displacement, $Δ u_{a} = u_{a} - u_{0}$ . If $c_{a}$ is greater than a fraction (1% by default) of the incremental displacement, Abaqus/Standard performs another iteration. Both convergence checks must be satisfied before a solution is said to have converged for that time increment.

If the solution from an iteration is not converged, Abaqus/Standard performs another iteration to try to bring the internal and external forces into balance. First, Abaqus/Standard forms the new stiffness, $K_{a}$ , for the structure based on the updated configuration, $u_{a}$ . This stiffness, together with the residual $R_{a}$ , determines another displacement correction, $c_{b}$ , that brings the system closer to equilibrium (point b in Figure 4).

Figure 4. Second iteration.

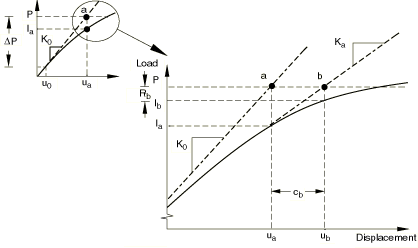
Abaqus/Standard calculates a new force residual, $R_{b}$ , using the internal forces from the structure's new configuration, $u_{b}$ . Again, the largest force residual at any degree of freedom, $R_{b}$ , is compared against the force residual tolerance, and the displacement correction for the second iteration, $c_{b}$ , is compared to the increment of displacement, $Δ u_{b}$ . If necessary, Abaqus/Standard performs further iterations. For more details on convergence in Abaqus/Standard, see Convergence criteria for nonlinear problems.

For each iteration in a nonlinear analysis Abaqus/Standard forms the model's stiffness matrix and solves a system of equations. Therefore, the computational cost of each iteration is close to the cost of conducting a complete linear analysis, making the computational expense of a nonlinear analysis potentially many times greater than the cost of a linear analysis. Since it is possible with Abaqus/Standard to save results at each converged increment, the amount of output data available from a nonlinear simulation can also be much greater than that available from a linear analysis of the same geometry.

Solution method

Abaqus/Standard by default uses the Newton's method to solve nonlinear problems iteratively (see section Convergence for a description). In some cases it uses an exact implementation of Newton's method, in the sense that the Jacobian or the stiffness matrix of the system is defined exactly, and quadratic convergence is obtained when the estimate of the solution is within the radius of convergence of the algorithm. In other cases the Jacobian is approximated so that the iterative method is not an exact Newton method. For example, some material and surface interface models (such as nonassociated flow plasticity models or Coulomb friction) create a nonsymmetric Jacobian matrix, but you may choose to approximate this matrix by its symmetric part.

Alternative techniques to the standard Newton method are available. These techniques attempt to reduce costs associated with assembly of the full Jacobian and its subsequent factorization during every iteration in the Newton method. The details of these techniques and the situations where they are applicable to derive performance gains are described in the following.

Specifying the quasi-Newton method

You can choose to use the quasi-Newton technique for a particular step (described in Quasi-Newton solution technique) instead of the standard Newton method for solving nonlinear equations.

The quasi-Newton technique can save substantial computational cost in some cases by reducing the number of times the Jacobian matrix is factorized. Generally it is most successful when the system is large and many iterations are needed per increment or when the stiffness matrix is not changing much from iteration to iteration (such as in a dynamic analysis using implicit time integration or in a small-displacement analysis with local plasticity). It can be used only for symmetric systems of equations; therefore, it cannot be used when the unsymmetric solver is specified for a step (see Defining an analysis), nor can it be used for procedures that always produce an unsymmetric system of equations, such as Fully coupled thermal-stress analysis and Abaqus/Aqua analysis. In addition, it cannot be used for a static Riks procedure (see Unstable collapse and postbuckling analysis).

The quasi-Newton method works well in combination with the line search method (see Improving the efficiency of the solution by using the line search algorithm). Line searches help to prevent divergence of equilibrium iterations resulting from the inexact Jacobian produced by the quasi-Newton method. The line search method is activated by default for steps that use the quasi-Newton method. You can override this action by specifying line search controls.

You can specify the number of quasi-Newton iterations allowed before the kernel matrix is reformed. The default number of iterations is 8. Additional matrix reformations may occur automatically during the iteration process depending on the convergence behavior. Since quadratic convergence is not expected during quasi-Newton iterations, the logarithmic rate of convergence check is not applied during the time incrementation. Furthermore, the iteration count used in the time incrementation is a weighted sum of quasi-Newton iterations, with the weight factor depending on whether or not a kernel matrix has been reformed.

Input File Usage

SOLUTION TECHNIQUE, TYPE=QUASI-NEWTON, REFORM KERNEL=n

Abaqus/CAE Usage

Step module: step editor: Other: Solution technique: Quasi-Newton, Number of iterations allowed before the kernel matrix is reformed: n

Specifying the separated method

Alternatively, you can choose to use the separated technique instead of the standard Newton method for solving nonlinear equations for fully coupled thermal-stress and coupled thermal-electrical procedures.

The separated technique (described in Fully coupled thermal-stress analysis and Coupled thermal-electrical analysis) approximates the Jacobian by eliminating interfield coupling terms and can save substantial computational cost in cases where there is relatively weak coupling between the fields.

Input File Usage

SOLUTION TECHNIQUE, TYPE=SEPARATED

Abaqus/CAE Usage

Step module: step editor: Other: Solution technique: Separated

Linear Complementarity Problem (LCP) solution technique for solving contact problems

Contact problems in Abaqus/Standard involve solving nonlinear equations in general nonlinear steps. For each load increment, the active set of contact constraints and corresponding contact stresses are solved for along with other solution variables (typically) using Newton iterations. For structural problems involving contact, an alternative solution technique is available under special modeling assumptions listed below.

Contact can be modeled entirely with the small sliding formulation with frictionless tangential behavior.
Symmetric stiffness matrix storage is applicable.
Except contact, the rest of the model response can be assumed to be linear.

Under these assumptions, the governing equations take the form of a set of linear inequality constraints from contact (contact gap has to be either positive or zero) along with a set of linear equations for equilibrium. The resulting mathematical problem is known as the Linear Complementarity Problem (LCP). The LCP technique solves for unknown active contact constraints and corresponding contact stresses together with displacement unknowns during the solution process. This solution technique is accessible only within a static perturbation step (see Contact within static perturbation analysis). The linearization of material and geometric nonlinearities at the base state is relied upon for ensuring linear response for the rest of the model automatically while nonlinearities only due to contact status changes are handled. Commonly, geometric nonlinearities are turned off as a modeling assumption while using the LCP approach.

The LCP solution involves the following phases. First, displacement degrees-of-freedom are condensed out and the governing equations are written only in terms of unknown contact pressure variables from potential contact constraints at the contact interfaces. The potential constraints are determined based on gap/overclosure distances at the base state prior to the LCP solution process. The condensation phase is followed by an iterative process (LCP iterations) to determine active contact constraints and the corresponding contact pressure values. The displacement solution is obtained from the contact pressure solution in a subsequent recovery phase. Global stiffness matrix assembly and solving the global set of equations during multiple nonlinear iterations in the traditional approach are avoided, which makes the LCP approach more efficient in some situations.

Input File Usage

Use the following option to activate the LCP solution technique:

SOLUTION TECHNIQUE,TYPE=LCP CONTACT

Abaqus/CAE Usage

The LCP solution technique is not supported in Abaqus/CAE.

Specifying a gap distance to control potential constraints exposed to the LCP solver

The number of potential constraints exposed to the LCP solver can be controlled by a gap distance that you specify. All closed contact constraints and those that are open and within the gap distance in the base state are included as potential constraints. By default, a gap distance is internally computed based on a characteristic facet dimension associated with individual contact pairs. You can also provide a scale factor to scale the gap distance that you specified or the internally computed defaults. The choice of the gap distance affects performance.

Choosing a conservative gap distance can rapidly increase the cost of the LCP solver since such costs show a cubic growth in the number of potential contact constraints. The LCP solver can automatically revise the gap distance while keeping a check on the number of potential constraints if it finds that the initial choice of the gap distance is small and results in overclosure violations. Therefore, it may not be necessary to be overly conservative while choosing the gap distance.

For an example of this technique, see Input file template.

Input File Usage

Use the following option to specify the gap distance that specifies the potential contact zone and a scale factor for the gap distance for the LCP solution technique:

SOLUTION TECHNIQUE,TYPE=LCP CONTACT
gap distance, scale factor

Abaqus/CAE Usage

The LCP solution technique is not supported in Abaqus/CAE.

Additional perspectives

Several examples are presented here for a better understanding of the performance characteristics of the LCP approach.

Figure 5 shows an example where a solid sphere is pinched between rigid plates. Linear elastic material behavior is assigned to the sphere, while the small-sliding formulation without friction is assumed for modeling contact. Geometric nonlinearities are turned off. This model is set up so that both the traditional and the LCP approaches are expected to give the same final solution. Boundary conditions are applied to push the top plate down in a static step for the traditional approach, and the same conditions are prescribed within a static perturbation step in the LCP approach. An initial guess of half the boundary displacement is specified for the gap distance to include potential contact constraints.

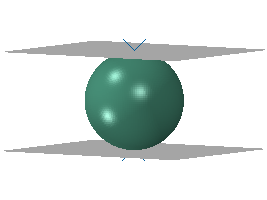
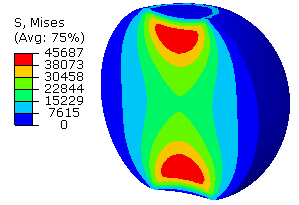
Figure 5. Pinching of a solid sphere solved with LCP contact.

Table 1 compares normalized wall times between the traditional and the LCP approaches for three different meshes for the model in Figure 5. The LCP approach shows significant speedups in this example.

Table 1. Performance comparison of LCP contact with traditional contact for a pinched sphere.
Quantity	Coarse mesh		Medium mesh		Fine mesh
Quantity	LCP approach	Traditional approach	LCP approach	Traditional approach	LCP approach	Traditional approach
Normalized wall time (speed up factor for LCP)	1.0	5.0 (5.0)	27.8	193 (6.9)	187	1925 (10.3)
Number of global assembly and solve iterations	1	7	1	9	1	10
Number of LCP iterations	134	Not applicable	492	Not applicable	1044	Not applicable
Model size	42,000		306,000		890,000
Number of potential contact constraints to LCP solver	353	Not applicable	1496	Not applicable	3476	Not applicable
Active constraints from the solution	187		743		1696

Consider instead a grid of spheres in Figure 6 made by assembling instances of the setup in the previous example. Three grids with 10, 50 and 100 spheres are considered for comparison purposes in Table 2. These models more closely approximate an assembly of parts. The meshes on the individual spheres correspond to the coarsest mesh in the previous example. The rest of the model definitions remain the same. From Table 2 it is clear that as the number of potential contact constraints increase, the cubic growth of the cost of the LCP solver starts to dominate. The performance degradation compared to the traditional approach is rapid as the grid size increases and becomes unacceptable for the 50 to the 100 sphere models.

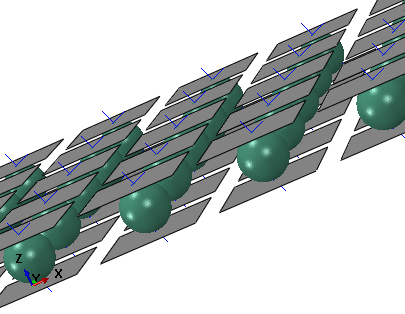
Figure 6. Pinching of multiple solid spheres.

Table 2. Performance comparison of LCP contact with traditional contact for a grid of pinched spheres.
Quantity	Single sphere		10 spheres		50 spheres		100 spheres
Quantity	LCP approach	Traditional approach	LCP approach	Traditional approach	LCP approach	Traditional approach	LCP approach	Traditional approach
Normalized wall time (speed up factor for LCP)	1	5 (5.0)	25	54 (2.2)	2,064	358 (0.17)	14,492	553 (0.038)
Number of global assembly and solve iterations	1	7	1	7	1	7	1	7
Number of LCP iterations	134	Not applicable	1214	Not applicable	6014	Not applicable	12014	Not applicable
Model size	42,000		420,000		2,100,000		4,200,000
Number of potential contact constraints to LCP solver	353	Not applicable	3,530	Not applicable	17,650	Not applicable	353,00
Active constraints from the solution	187		1,870		9,350		18,700

Keep the following additional points in mind when using the LCP approach:

The performance gains with the LCP approach are problem dependent. In general, the number of potential contact constraints exposed to the LCP solver should be small compared to the overall problem size. In addition, the performance of the LCP solver can start to degrade when the number of potential constraints exceeds 10,000 as seen in larger contact models. The LCP approach can be beneficial if the Newton iterations using the traditional approach are expensive; for example, if you are using the direct sparse solver, costs add up quickly when dealing with a stiffness matrix from a blocky structure (see The sparse solver).
For various mesh sizes that result in small- to medium-sized problems as in Table 1, direct solver costs in the traditional approach tend to dominate the LCP costs. On the other hand, for an assembly of components, the resulting stiffness matrix typically exhibits a higher degree of sparsity. The direct sparse solver costs and, thereby, the Newton iteration costs can be much smaller compared to a similarly sized blocky model. In those cases, the traditional approach is usually more efficient.
The cost of LCP iterations also depends on how far the final solution for actual active constraints differs from the potential constraints. For example, if the active contact constraints in the final solution are a small subset of the potential constraints, more LCP iterations are necessary to arrive at the final solution than in a problem where the initial guess is close to the final solution. On the other hand, if the initial gap distance is too small, the gap distance may have to be revised and the set of potential constraints expanded. The LCP iterations in this case are repeated with the new set of potential constraints, thereby increasing the cost of the LCP approach.
The LCP iterations may have difficulty converging in cases where the stiffness matrix in the base state shows ill-conditioning or corresponds to instabilities. It is also necessary to ensure sufficient boundary restraints to avoid stiffness matrix singularities in the base state.
To gain a better understanding of solution accuracy and efficiency, you may choose to compare the solution to the fully nonlinear problem with the solution from the LCP approach for the types of problems you want to solve. This ensures that ignoring various nonlinearities would still provide an adequate solution. In traditional applications where nonlinear effects and friction may be important, the modeling assumptions imposed by LCP approach may be too restrictive for its effective use.

Automatic incrementation control

By default, Abaqus/Standard automatically adjusts the size of the time increments to solve nonlinear problems efficiently. You need to suggest only the size of the first increment in each step of the simulation, after which Abaqus/Standard automatically adjusts the size of the increments. If you do not provide a suggested initial increment size, Abaqus/Standard will attempt to apply all of the loads defined in the step in a single increment. For highly nonlinear problems Abaqus/Standard will have to reduce the increment size repeatedly to obtain a solution, resulting in wasted CPU time. It is advantageous to provide a reasonable initial increment size because only in mildly nonlinear problems can all of the loads in a step be applied in a single increment.

The number of iterations needed to find a converged solution for a time increment will vary depending on the degree of nonlinearity in the system. With the default incrementation control, the procedure works as follows. If the solution has not converged within 16 iterations or if the solution appears to diverge, Abaqus/Standard abandons the increment and starts again with the increment size set to 25% of its previous value. It then attempts to find a converged solution with this smaller time increment. If the solution still fails to converge, Abaqus/Standard reduces the increment size again. This process is continued until a solution is found. If the time increment becomes smaller than the minimum you defined or more than 5 attempts are needed, Abaqus/Standard stops the analysis.

If the increment converges in fewer than 5 iterations, this indicates that the solution is being found fairly easily. Therefore, Abaqus/Standard automatically increases the increment size by 50% if 2 consecutive increments require fewer than 5 iterations to obtain a converged solution.

While the default automatic incrementation control is suitable for most analyses, you can change all the defaults when necessary by specifying solution controls; see Commonly used control parameters and Time integration accuracy in transient problems.

Automatic stabilization of unstable problems

Nonlinear static problems can be unstable. Such instabilities may be of a geometrical nature, such as buckling, or of a material nature, such as material softening. If the instability manifests itself in a global load-displacement response with a negative stiffness, the problem can be treated as a buckling or collapse problem as described in Unstable collapse and postbuckling analysis. However, if the instability is localized, there will be a local transfer of strain energy from one part of the model to neighboring parts, and global solution methods may not work. This class of problems has to be solved either dynamically or with the aid of (artificial) damping; for example, by using dashpots.

Abaqus/Standard provides an automatic mechanism for stabilizing unstable quasi-static problems through the automatic addition of volume-proportional damping to the model. The applied damping factors can be constant over the duration of a step, or they can vary with time to account for changes over the course of a step. The latter, adaptive approach is typically preferred.

Automatic stabilization of static problems with a constant damping factor

Automatic stabilization with a constant damping factor is triggered by including automatic stabilization in any nonlinear quasi-static procedure. Viscous forces of the form

F_{v} = c M^{*} v

are added to the global equilibrium equations

P - I - F_{v} = 0,

where $M^{*}$ is an artificial mass matrix calculated with unity density, c is a damping factor, $v = Δ u / Δ t$ is the vector of nodal velocities, and $Δ t$ is the increment of time (which may or may not have a physical meaning in the context of the problem being solved).

For the case of static stabilization the mass matrix for Timoshenko beams is always calculated assuming isotropic rotary inertia, regardless of the type of rotary inertia specified for the beam section definition (Rotary inertia for Timoshenko beams).

Automatic stabilization does not carry over automatically to subsequent steps. It needs to be declared for any step in which you want it to be active. Abaqus/Standard recalculates new values for the damping factor, based on the declared damping intensity and on the solution of the first increment of the step. Therefore, unless you specify the same damping factor directly (see Directly specifying the damping factor below), an analysis with an unstable step may produce slightly different results from the same analysis with the original step split into two steps. Moreover, if the instabilities in the model have not subsided by the end of a step, viscous forces may be terminated abruptly or modified at the beginning of subsequent steps, potentially causing convergence difficulties if automatic stabilization is not used in the subsequent step. If such a situation arises, it is recommended that the problem be restarted with the damping factor set equal to the value chosen by Abaqus/Standard (or to the value you specified) in the previous step. This value is printed in the message (.msg) file for the previous step. If it is necessary to have an accurate static equilibrium solution after an instability has occurred (and the model's behavior has returned to a stable regime), the step with automatic stabilization can be followed by a step without such stabilization.

Calculating the damping factor based on the dissipated energy fraction

It is assumed that the problem is stable at the beginning of the step and that instabilities may develop in the course of the step. While the model is stable, viscous forces and, therefore, the viscous energy dissipated are very small. Thus, the additional artificial damping has no effect. If a local region goes unstable, the local velocities increase and, consequently, part of the strain energy then released is dissipated by the applied damping. Abaqus/Standard can, if necessary, reduce the time increment to permit the process to occur without the unstable response causing very large displacements. Abaqus/Standard calculates and prints to the message file the damping factor, c, based on the solution of the first increment of a step. In most applications the first increment of the step is stable without the need to apply damping. The damping factor is then determined in such a way that the dissipated energy for a given increment with characteristics similar to the first increment is a small fraction of the extrapolated strain energy. The fraction is called the dissipated energy fraction and has a default value of 2.0 × 10⁻⁴. If the default value for the dissipated energy fraction is used, the adaptive automatic stabilization scheme discussed in the next section will be activated automatically by default in the step.

Alternatively, you can specify the non-default dissipated energy fraction for automatic stabilization directly.

Input File Usage

Use any of the following options to specify a nondefault dissipated energy fraction:

COUPLED TEMPERATURE-DISPLACEMENT, STABILIZE=dissipated energy fraction
SOILS, STABILIZE=dissipated energy fraction
STATIC, STABILIZE=dissipated energy fraction
STEADY STATE TRANSPORT, STABILIZE=dissipated energy fraction
VISCO, STABILIZE=dissipated energy fraction

Abaqus/CAE Usage

Step module: Create Step: General: any valid step type: Basic: select Specify dissipated energy fraction from the Automatic stabilization field

Considerations when the first increment is unstable or singular

There are cases where the first increment is either unstable or singular (due to a rigid body mode). In such cases it is not possible to obtain a solution to the first increment without applying some damping. Therefore, some damping is already applied during the first increment. The damping factor used for the initial increment is chosen such that the average element damping matrix component, divided by the step time, is equal to the average element stiffness matrix component multiplied by the dissipated energy fraction. If the calculated strain energy change in this increment indicates that the solution without damping is stable, the damping factor is recalculated based upon the energy method described previously. However, if the strain energy change indicates that the solution is unstable or singular, the initially calculated damping factor is maintained, and a warning message is issued indicating that the amount of damping applied may not be appropriate. In many cases the amount of damping may actually be rather large, which can affect the solution in ways that are not desirable. Therefore, if the above mentioned warning message is issued, check the viscous forces (VF) and compare them with the expected nodal forces to make sure that the viscous forces do not dominate the solution. If necessary, follow the stabilized step with another step in which stabilization is not used or with a step in which a much smaller damping factor is used.

Directly specifying the damping factor

You can also specify the damping factor directly. Unfortunately, it is generally quite difficult to make a reasonable estimate for the damping factor unless a value is known from the output of previous runs; the damping factor depends not only on the amount of damping but also on mesh size and material behavior.

Input File Usage

Use any of the following options to specify the damping factor directly:

COUPLED TEMPERATURE-DISPLACEMENT, STABILIZE, FACTOR=damping factor
SOILS, STABILIZE, FACTOR=damping factor
STATIC, STABILIZE, FACTOR=damping factor
STEADY STATE TRANSPORT, STABILIZE, FACTOR=damping factor
VISCO, STABILIZE, FACTOR=damping factor

Abaqus/CAE Usage

Step module: Create Step: General: Coupled temp-displacement, Soils, Static, General, or Visco: Basic: select Specify damping factor from the Automatic stabilization field

Adaptive automatic stabilization scheme

As discussed above, the automatic stabilization scheme with a constant damping factor typically works well to subside instabilities and to eliminate rigid body modes without having a major effect on the solution. However, there is no guarantee that the value of the damping factor is optimal or even suitable in some cases. This is particularly true for thin shell models, in which the damping factor may be too high when a poor estimation of the extrapolated strain energy is made during the first increment. For such models you may have to increase the damping factor if the convergence behavior is problematic or to decrease the damping factor if it distorts the solution. The former case would require you to rerun the analysis with a larger damping factor, while the latter case would require you to perform postanalysis comparison of the energy dissipated by viscous damping (ALLSD) to the total strain energy (ALLIE). Therefore, obtaining an optimal value for the damping factor is a manual process requiring trial and error until a converged solution is obtained and the dissipated stabilization energy is sufficiently small.

The adaptive automatic stabilization scheme, in which the damping factor can vary spatially and with time, provides an effective alternative approach. In this case the damping factor is controlled by the convergence history and the ratio of the energy dissipated by viscous damping to the total strain energy. If the convergence behavior is problematic because of instabilities or rigid body modes, Abaqus/Standard automatically increases the damping factor. For example, the damping factor may increase if an analysis takes extra severe discontinuity or equilibrium iterations per increment or requires time increment cutbacks. On the other hand, Abaqus/Standard may reduce the damping factor automatically if instabilities and rigid body modes subside.

The ratio of the energy dissipated by viscous damping to the total strain energy is limited by an accuracy tolerance that you specify. Such an accuracy tolerance is imposed on the global level for the whole model. If the ratio of the energy dissipated by viscous damping to the total strain energy for the whole model exceeds the accuracy tolerance, the damping factor at each individual element is adjusted to ensure that the ratio of the stabilization energy to the strain energy is less than the accuracy tolerance on both the global and local element level. The stabilization energy always increases, while the strain energy may decrease. Therefore, Abaqus/Standard restricts the ratio of the incremental value of the stabilization energy to the incremental value of the strain energy for each increment to ensure that this value has not exceeded the accuracy tolerance if the ratio of the total stabilization energy to the total strain energy exceeds the accuracy tolerance. The accuracy tolerance is a targeted value and can be exceeded in some situations, such as when there is rigid body motion or when significant non-local instability occurs.

The default accuracy tolerance used by the adaptive automatic stabilization scheme is 0.05. The default tolerance is suitable for most applications, but you have the option of specifying a nondefault accuracy tolerance if necessary. If the accuracy tolerance is set equal to zero, the adaptive automatic stabilization scheme is not activated and the automatic stabilization scheme with a constant damping factor will be used in the step.

If the accuracy tolerance is not specified but the dissipated energy fraction with the default value of 2.0 × 10⁻⁴ is used, the adaptive automatic damping algorithm will be activated automatically with an accuracy tolerance of 0.05.

Input File Usage

Use any of the following options to activate adaptive automatic stabilization with the default stabilization energy tolerance:

COUPLED TEMPERATURE-DISPLACEMENT, STABILIZE
SOILS, STABILIZE
STATIC, STABILIZE
STEADY STATE TRANSPORT, STABILIZE
VISCO, STABILIZE

Use any of the following options to activate adaptive automatic stabilization with a nondefault stabilization energy tolerance:

COUPLED TEMPERATURE-DISPLACEMENT, STABILIZE,
 ALLSDTOL=accuracy tolerance
SOILS, STABILIZE, ALLSDTOL=accuracy tolerance
STATIC, STABILIZE, ALLSDTOL=accuracy tolerance
STEADY STATE TRANSPORT, STABILIZE, 
   ALLSDTOL=accuracy tolerance
VISCO, STABILIZE, ALLSDTOL=accuracy tolerance

Abaqus/CAE Usage

Step module: Create Step: General: Coupled temp-displacement, Soils, Static, General, or Visco: Basic: select an Automatic stabilization method: toggle on Use adaptive stabilization with max. ratio of stabilization to strain energy: accuracy tolerance

Default value of the initial damping factor

By default, the initial value of the damping factor is typically equal to the value that would be used for automatic stabilization with a constant damping factor (see Calculating the damping factor based on the dissipated energy fraction above). In some cases additional factors that are considered with adaptive automatic stabilization cause some differences in the initial damping factor.

Specifying the initial damping factor directly

Alternatively, you can specify the initial damping factor directly. The damping factor is adjusted based on the convergence history and the accuracy tolerance through the step.

Input File Usage

Use any of the following options to specify the initial damping factor directly with the default stabilization energy tolerance:

COUPLED TEMPERATURE-DISPLACEMENT, STABILIZE, FACTOR=damping factor, ALLSDTOL
SOILS, STABILIZE, FACTOR=damping factor, ALLSDTOL
STATIC, STABILIZE, FACTOR=damping factor, ALLSDTOL
STEADY STATE TRANSPORT, STABILIZE, FACTOR=damping factor, 
ALLSDTOL
VISCO, STABILIZE, FACTOR=damping factor, ALLSDTOL

Abaqus/CAE Usage

Step module: Create Step: General: Coupled temp-displacement, Soils, Static, General, or Visco: Basic: from the Automatic stabilization field, select Specify damping factor: damping factor: toggle on Use adaptive stabilization with max. ratio of stabilization to strain energy: maximum ratio

Propagating the damping factors from the immediately preceding general step into the current step

Adaptive automatic stabilization provides an option to propagate the damping factors from the immediately preceding general step to the subsequent steps. The default is to not propagate the damping factors from the results of the preceding general step. In this case Abaqus recalculates the initial damping factors based on the declared dissipated energy faction and on the solution of the first increment of the step, or you can specify the initial damping factors directly.

Input File Usage

Use any of the following options to indicate that the damping factors in the current step are propagated from the immediately preceding general step:

COUPLED TEMPERATURE-DISPLACEMENT, STABILIZE, ALLSDTOL, CONTINUE=YES
SOILS, STABILIZE, ALLSDTOL, CONTINUE=YES
STATIC, STABILIZE, ALLSDTOL, CONTINUE=YES
STEADY STATE TRANSPORT, STABILIZE, ALLSDTOL, 
CONTINUE=YES
VISCO, STABILIZE, ALLSDTOL, CONTINUE=YES

Abaqus/CAE Usage

Step module: Create Step: General: Coupled temp-displacement, Soils, Static, General, or Visco: Basic: select Use damping factors from previous general step from the Automatic stabilization field: Use adaptive stabilization with max. ratio of stabilization to strain energy: accuracy tolerance

Ensuring that an accurate solution is obtained with automatic stabilization

Whenever automatic stabilization is applied to a problem, check the following to ensure that accurate solutions are obtained:

For a damping factor calculated using the dissipated energy fraction, check the factor printed to the message (.msg) file at the end of the first increment to ensure that a reasonable amount of damping is applied. Unfortunately, the damping factor is problem dependent; therefore, you must rely on experience from previous runs.
Compare the viscous forces (VF) with the overall forces in the analysis, and ensure that the viscous forces are relatively small compared with the overall forces in the model.
Compare the viscous damping energy (ALLSD) with the total strain energy (ALLIE), and ensure that the ratio does not exceed the dissipated energy fraction or any reasonable amount. The viscous damping energy may be large if the structure undergoes a large amount of motion.

The automated procedure of computing damping factors works well for many applications. However, there are cases where the computed damping factor is either too small, thus not controlling the instability, or too high, thus leading to inaccurate results. These problems are more likely to occur when using a constant damping factor—the damping factor is computed in the first increment, which may not be representative of behavior in the rest of the step. For example, consider a sequentially coupled thermal-stress analysis in which a mechanical analysis reads temperatures from a previous transient thermal analysis. Typically the thermal analysis exhibits a diffusive process, where rapid changes in temperature occurs early in the analysis and minor changes in temperature occur once steady state is reached. In such a case Abaqus will compute the extrapolated strain energy based on the temperatures corresponding to the time of the first increment (in this case there may be a significant change in temperature for the first increment), thus yielding a larger then expected extrapolated strain energy. This in turn leads to a damping factor that is too large, resulting in inaccurate results.

If one of the automatic stabilization methods is not working appropriately, you can try using the other automatic stabilization method; the adaptive stabilization scheme is generally preferred. Alternatively, you can try directly specifying the damping factor.

Input file template

The following template shows an example of specifying a gap distance to control potential constraints exposed to the LCP solver.

HEADING
…
STEP,PERTURBATION
STATIC
Data line to define time incrementation parameters
SOLUTION TECHNIQUE,TYPE=LCP CONTACT
Optional data line to define a gap distance and a gap scaling factor
LOAD CASE,NAME=Case1
CLOAD
Data line(s) to define concentrated loads for the first load case
END LOAD CASE 
**
LOAD CASE,NAME=Case2
BOUNDARY
Data line(s) to define boundary displacements for the second load case
END LOAD CASE 
…
END STEP