Preprocessing—creating the model with Abaqus/CAE | ||
| ||
-
A Python script for this example is provided in Forming a channel. Instructions on how to fetch the script and run it within Abaqus/CAE are given in Example Files.
-
A plug-in script for this example is available in the Abaqus/CAE Plug-in toolset. To run the script from Abaqus/CAE, select ; highlight Forming a channel; and click . For more information about the Getting Started plug-ins, see Running the Getting Started with Abaqus examples.
- Part definition
-
Start Abaqus/CAE (if you are not already running it). You will have to create four parts: a deformable part representing the blank and three rigid parts representing the tools.
- Deformable blank
-
Create a two-dimensional, deformable solid part with a planar shell base feature to represent the deformable blank. Use an approximate part size of 0.25, and name the part Blank. To define the geometry, sketch a rectangle of arbitrary dimensions. Then, dimension the horizontal and vertical lengths of the rectangle, and edit the dimensions to define the part geometry precisely. The final sketch is shown in Figure 1.
Figure 1. Sketch of the deformable blank (with grid spacing doubled).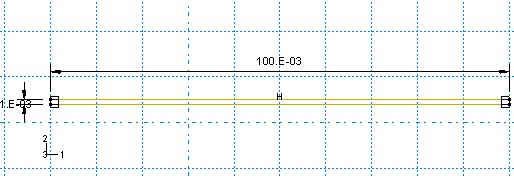
- Rigid tools
-
You must create a separate part for each rigid tool. Each of these parts will be created using very similar techniques so it is sufficient to consider the creation of only one of them (for example, the punch) in detail. Create a two-dimensional planar, analytical rigid part with a wire base feature to represent the rigid punch. Use an approximate part size of 0.25, and name the part Punch. Using the Create Lines and Create Fillet tools, sketch the geometry of the part. Create and edit the dimensions as necessary to define the geometry precisely. The final sketch is shown in Figure 2.
Figure 2. Sketch of the rigid punch (with grid spacing doubled).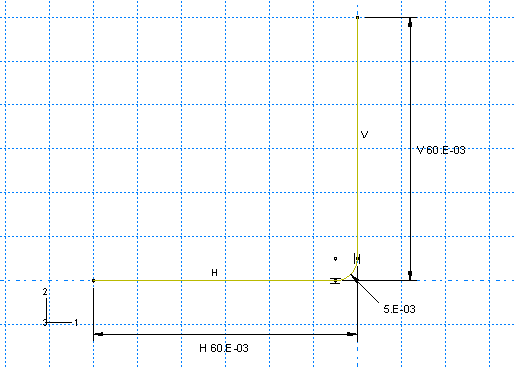
A rigid body reference point must be created. Exit the Sketcher when you are finished defining the part geometry to return to the Part module. From the main menu bar, select . In the viewport, select the point at the center of the arc as the rigid body reference point.
Next, create two additional analytical rigid parts named Holder and Die, representing the blank holder and rigid die, respectively. Since the parts are mirror images of each other, the easiest way to define the geometry of the new parts is to rotate the sketch created for the punch. (The Copy Part tool cannot be used to mirror analytical rigid parts.) For example, edit the punch feature section sketch, and save this sketch with the name Punch. Then, create a part named Holder, and add the Punch sketch to the part definition. Mirror the sketch about the vertical edge. Finally, create a part named Die, and add the Punch sketch to the part definition. In this case mirror the sketch twice: first about the vertical edge and then about the horizontal edge. Be sure to create a reference point at the center of the arc on each part.
- Material and section properties
-
The blank is made from a high-strength steel (elastic modulus of 210.0 × 109 Pa, = 0.3). Its inelastic stress-strain behavior is tabulated in Table 1 and shown in Figure 3. The material undergoes considerable work hardening as it deforms plastically. It is likely that plastic strains will be large in this analysis; therefore, hardening data are provided up to 50% plastic strain.
Table 1. Yield stress–plastic strain data. Yield stress (Pa) Plastic strain 400.0E6 0.0 420.0E6 2.0E−2 500.0E6 20.0E−2 600.0E6 50.0E−2 Figure 3. Yield stress vs. plastic strain.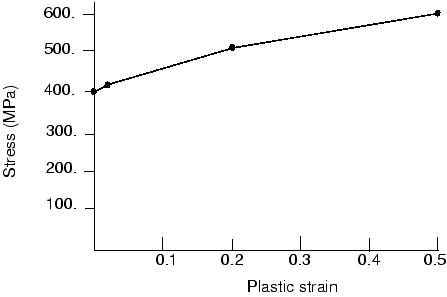
Create a material named Steel with these properties. Create a homogeneous solid section named BlankSection that refers to the material Steel. Assign the section to the blank.
The blank is going to undergo significant rotation as it deforms. Reporting the values of stress and strain in a coordinate system that rotates with the blank's motion will make it much easier to interpret the results. Therefore, a local material coordinate system that is aligned initially with the global coordinate system but moves with the elements as they deform should be created. To do this, create a rectangular datum coordinate system using the Create Datum CSYS: 3 Points
 tool. From the main menu bar of the
Property module,
select . Select the blank as the region to which
the local material orientation will be assigned, and pick the datum coordinate
system in the viewport as the CSYS (select Axis
3 and accept None for the additional rotation
options).
tool. From the main menu bar of the
Property module,
select . Select the blank as the region to which
the local material orientation will be assigned, and pick the datum coordinate
system in the viewport as the CSYS (select Axis
3 and accept None for the additional rotation
options).
- Assembling the parts
-
You will now create an assembly of part instances to define the analysis model. Begin by instancing the blank. Then, instance and position the rigid tools using the techniques described below.
To instance and position the punch:
-
In the Model Tree, double-click Instances underneath the Assembly container and select Punch as the part to instance.
Two-dimensional plane strain models must be defined in the global 1–2 plane. Therefore, do not rotate the parts after they have been instanced. You may, however, place the origin of the model at any convenient location. The 1-direction will be normal to the symmetry plane.
-
The bottom of the punch initially rests on top of the blank, as indicated in Figure 2. From the main menu bar, select to position the punch vertically with respect to the blank.
-
Choose the horizontal edge of the punch as the straight edge of the movable instance and the edge on the top of the blank as the straight edge of the fixed instance.
Arrows appear on both instances. The punch will be moved so that its arrow points in the same direction as the arrow on the blank.
-
If necessary, click in the prompt area to reverse the direction of the arrow on the punch so that both arrows point in the same direction; otherwise, the punch will be flipped. When both arrows point in the same direction, click .
-
Enter a distance of 0.0 m to specify the separation between the instances.
The punch is moved in the viewport to the specified location. Click the Auto-fit tool
 so that the entire assembly is rescaled to fit in the viewport.
so that the entire assembly is rescaled to fit in the viewport.
-
The vertical edge of the punch is 0.05 m from the left edge of the blank, as shown in Figure 2. Define another constraint to position the punch horizontally with respect to the blank.
Select the vertical edge of the punch as the straight edge of the movable instance and the left edge of the blank as the straight edge of the fixed instance. Flip the arrow on the punch if necessary so that both arrows point in the same direction. Enter a distance of −0.05 m to specify the separation between the edges. (A negative distance is used since the offset is applied in the direction of the edge normal. The edge normal points away from the edge of the blank.)
Now that you have positioned the punch relative to the blank, check to make sure that the left end of the punch extends beyond the left edge of the blank. This is necessary to prevent any nodes associated with the blank from “falling off” the rigid surface associated with the punch during the contact calculations. If necessary, return to the Part module and edit the part definition to satisfy this requirement.
- To instance and position the blank holder:
-
The procedure for instancing and positioning the holder is very similar to that used to instance and position the punch. Referring to Figure 2, we see that the holder is initially positioned so that its horizontal edge is offset a distance of 0.0 m from the top edge of the blank and its vertical edge is offset a distance of 0.001 m from the vertical edge of the punch. Define the necessary constraints to position the blank holder. Remember to flip the directions of the arrows as necessary, and make sure the right end of the holder extends beyond the right edge of the blank. If necessary, return to the Part module and edit the part definition.
- To instance and position the die:
-
The procedure for instancing and positioning the die is very similar to that used to instance and position the other tools. Referring to Figure 2, we see that the die is initially positioned so that its horizontal edge is offset a distance of 0.0 m from the bottom edge of the blank and its vertical edge is offset a distance of 0.0 m from the vertical edge of the holder. Define the necessary constraints to position the die. Remember to flip the directions of the arrows as necessary, and make sure the right end of the die extends beyond the right edge of the blank. If necessary, return to the Part module and edit the part definition.
The final assembly is shown in Figure 4.
Figure 4. Model assembly.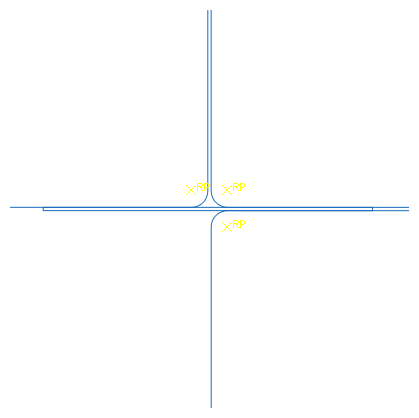
-
- Geometry sets
-
At this point it is convenient to create the geometry sets that will be used to specify loads and boundary conditions and to restrict data output. Four sets should be created: one at each rigid body reference point, and one at the symmetry plane of the blank.
To create geometry sets:
-
Double-click the Sets item underneath the Assembly container to create the following geometry sets:
-
RefPunch at the punch rigid body reference point.
-
RefHolder at the holder rigid body reference point.
-
RefDie at the die rigid body reference point.
-
Center at the left vertical edge (symmetry plane) of the blank.
-
-
- Defining steps and output requests
-
There are two major sources of difficulty in Abaqus/Standard contact analyses: rigid body motion of the components before contact conditions constrain them and sudden changes in contact conditions, which lead to severe discontinuity iterations as Abaqus/Standard tries to establish the correct condition of all contact surfaces. Therefore, wherever possible, take precautions to avoid these situations.
Removing rigid body motion is not particularly difficult. Simply ensure that there are enough constraints to prevent all rigid body motions of all the components in the model. This may mean using boundary conditions initially to get the components into contact, instead of applying loads directly. Using this approach may require more steps than originally anticipated, but the solution of the problem should proceed more smoothly.
Alternatively, contact controls can be used to stabilize rigid body motion automatically. With this approach Abaqus/Standard applies viscous damping to the slave nodes of the contact pair. Care must be taken, however, to ensure that the viscous damping does not significantly alter the physics of the problem, as will be the case if the dissipated stabilization energy and contact damping stresses are sufficiently small.
The channel-forming simulation will consist of two steps. Since the simulation involves material, geometric, and boundary nonlinearities, general steps must be used. In addition, the forming process is quasi-static; thus, we can ignore inertia effects throughout the simulation. Rather than use additional steps to establish firm contact, contact stabilization as described above will be used. A brief summary of each step (including the details of its purpose, definition, and associated output requests) is given below. However, the details concerning how the loads and boundary conditions are applied are discussed later.
- Step 1
-
The magnitude of the blank holder force is a controlling factor in many forming processes; therefore, it needs to be introduced as a variable load in the analysis. In this step the blank holder force will be applied.
Given the quasi-static nature of the problem and the fact that nonlinear response will be considered, create a static, general step named Holder force after the Initial step. Enter the following description for the step, Apply holder force; and include the effects of geometric nonlinearity. Set the initial time increment to 0.05 and the total time period to 1.0. Specify that the preselected field output be written every 20 increments for this step. In addition, request that the vertical reaction force and displacement (RF2 and U2) at the punch reference point (geometry set RefPunch) be written every increment as history data. In addition, write contact diagnostics to the message file ().
- Step 2
-
In the second and final step the punch will be moved down to complete the forming operation.
Create a static, general step named Move punch, and insert it after the Holder force step. Enter the following description for the step: Apply punch stroke. Because of the frictional sliding, the changing contact conditions, and the inelastic material behavior, there is significant nonlinearity in this step; therefore, set the maximum number of increments to a large value (for example, 1000). Set the initial time increment to 0.05 and the total time period to 1.0. Your output requests from the previous step will be propagated to this step. In addition, request that the restart file be written every 200 increments for this step.
- Monitoring the value of a degree of freedom
-
You can request that Abaqus monitor the value of a degree of freedom at one selected point. The value of the degree of freedom is shown in the Job Monitor and is written at every increment to the status (.sta) file and at specific increments during the course of an analysis to the message (.msg) file. In addition, a plot of the degree of freedom value over time appears in a new viewport that is generated automatically when you submit the analysis. You can use this information to monitor the progress of the solution.
In this model you will monitor the vertical displacement (degree of freedom 2) of the punch's reference node throughout each step. Before proceeding, make the first analysis step (Holder force) active by selecting it from the Step list located in the context bar. The monitor definition applied for this step will be propagated automatically to the subsequent step.
To select a degree of freedom to monitor:
-
From the main menu bar of the Step module, select .
The DOF Monitor dialog box appears.
-
Toggle on Monitor a degree of freedom throughout the analysis.
-
Click
 to select the region. In the prompt area, click
Points. In the Region Selection
dialog box that appears, select RefPunch; and click
Continue.
to select the region. In the prompt area, click
Points. In the Region Selection
dialog box that appears, select RefPunch; and click
Continue.
-
In the Degree of freedom text field, enter 2.
-
Accept the default frequency (every increment) at which this information will be written to the message file.
-
Click to exit the DOF Monitor dialog box.
-
- Defining contact interactions
-
Contact must be defined between the top of the blank and the punch, the top of the blank and the blank holder, and the bottom of the blank and the die. The rigid surface must be the master surface in each of these contact interactions. Each contact interaction must refer to a contact interaction property that governs the interaction behavior.
In this example we assume that the friction coefficient is zero between the blank and the punch. The friction coefficient between the blank and the other two tools is assumed to be 0.1. Therefore, two contact interaction properties must be defined: one with friction and one without.
Define the following surfaces: BlankTop on the top edge of the blank; BlankBot on the bottom edge of the blank; DieSurf on the side of the die that faces the blank; HolderSurf on the side of the holder that faces the blank; and PunchSurf on the side of the punch that faces the blank.
Tip: To facilitate your selections, you can selectively hide part instances using the Model Tree: expand the Instances container, highlight the part instances that you want to hide, and click mouse button 3. From the menu that appears, select Hide. To restore the visibility of the part instances, repeat the procedure, and select Show from the menu. Now define two contact interaction properties. (In the Model Tree, double-click the Interaction Properties container to create a contact property.) Name the first one NoFric; since frictionless contact is the default in Abaqus, accept the default property settings for the tangential behavior (select in the Edit Contact Property dialog box). The second property should be named Fric. For this property use the Penalty friction formulation with a friction coefficient of 0.1.
To alleviate convergence difficulties that may arise due to the changing contact states (in particular for contact between the punch and the blank), create contact controls to invoke automatic contact stabilization. Scale down the default damping factor by a factor of 1,000 to minimize the effects of stabilization on the solution. The procedure is described next.
To define contact controls:
-
In the Model Tree, double-click the Contact Controls container to define the contact controls.
The Create Contact Controls dialog box appears.
-
Name the control stabilize. Select Abaqus/Standard contact controls, and click Continue.
-
In the Stabilization tabbed page of the Edit Contact Controls dialog box, toggle on Automatic stabilization and set the Factor to 0.001.
-
Click to exit the Edit Contact Controls dialog box.
Finally, define the interactions between the surfaces and refer to the appropriate contact interaction property for each definition. (In the Model Tree, double-click the Interactions container to define a contact interaction.) In all cases define the interactions in the Initial step and use the Surface-to-surface contact (Standard) type. When defining the interactions, use the default finite-sliding formulation. The following interactions should be defined:
-
Die-Blank between surfaces DieSurf (master) and BlankBot (slave) referring to the Fric contact interaction property. Accept the default contact controls.
-
Holder-Blank between surfaces HolderSurf (master) and BlankTop (slave) referring to the Fric contact interaction property. Accept the default contact controls.
-
Punch-Blank between surfaces PunchSurf (master) and BlankTop (slave) referring to the NoFric contact interaction property. Using the Interaction Manager, edit this interaction to assign the nondefault contact controls defined earlier (stabilize) in the second analysis step (Move punch).
-
- Boundary conditions and loading for Step 1
-
In this step contact will be established between the blank holder and the blank while the punch and die are held fixed.
Constrain the blank holder in degrees of freedom 1 and 6, where degree of freedom 6 is the rotation in the plane of the model; constrain the punch and die completely. All of the boundary conditions for the rigid surfaces are applied to their respective rigid body reference nodes. Apply symmetric boundary constraints on the region of the blank lying on the symmetry plane (geometry set Center).
Table 2 summarizes the boundary conditions applied in this step.
Table 2. Summary of boundary conditions applied in Step 1. BC Name Geometry Set BCs CenterBC Center XSYMM RefDieBC RefDie U1 = U2 = UR3 = 0.0 RefHolderBC RefHolder U1 = UR3 = 0.0 RefPunchBC RefPunch U1 = U2 = UR3 = 0.0 To apply the blank holder force, create a mechanical concentrated force named RefHolderForce. Recall that in this simulation the required blank holder force is 440 kN. Thus, apply the load to set RefHolder, and specify a magnitude of −440.E3 for CF2.
- Boundary conditions for Step 2
-
In this step move the punch down to complete the forming operation. Using the Boundary Condition Manager, edit the RefPunchBC boundary condition to specify a value of −0.030 for U2, which represents the total displacement of the punch.
Before continuing, change the name of your model to Standard.
- Mesh creation and job definition
-
You should consider the type of element you will use before you design your mesh. When choosing an element type, you must consider several aspects of your model such as the model's geometry, the type of deformation that will be seen, the loads being applied, etc. The following points are important to consider in this simulation:
-
The contact between surfaces. Whenever possible, first-order elements (with the exception of tetrahedral elements) should be used for contact simulations. When using tetrahedral elements, second-order tetrahedral elements should be used for contact simulations (use either the regular or modified form for the surface-to-surface discretization, and use the modified form for the node-to-surface discretization).
-
Significant bending of the blank is expected under the applied loading. Fully integrated first-order elements exhibit shear locking when subjected to bending deformation. Therefore, either reduced-integration or incompatible mode elements should be used.
Either incompatible mode or reduced-integration elements are suitable for this analysis. In this analysis you will use reduced-integration elements with enhanced hourglass control. Reduced-integration elements help decrease the analysis time, and enhanced hourglass control reduces the possibility of hourglassing in the model. Mesh the blank with CPE4R elements using enhanced hourglass control (see Figure 5).
Figure 5. Mesh for the channel forming analysis.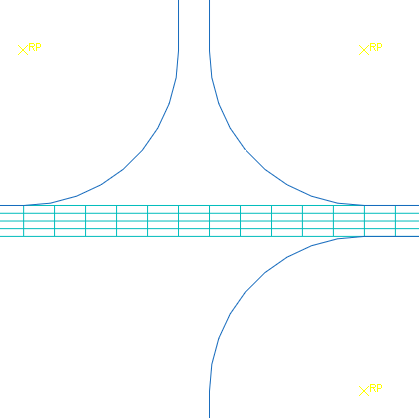
Seed the edges of the blank by specifying the number of elements along each edge. Specify 100 elements along the horizontal edges of the blank and 4 elements along each vertical edge of the blank. The tools have been modeled with analytical rigid surfaces so they need not be meshed. However, if the tools had been modeled with discrete rigid elements, the mesh would have to be sufficiently refined to avoid contact convergence difficulties. For example, if the die were modeled with R2D2 elements, the curved corner should be modeled with at least 20 elements. This would create a sufficiently smooth surface that would capture the corner geometry accurately. Always use a sufficient number of elements to model such curves when using discrete rigid elements.
Create a job named Channel. Give the job the following description: Analysis of the forming of a channel. Save your model to a model database file, and submit the job for analysis. Monitor the solution progress, correct any modeling errors that are detected, and investigate the cause of any warning messages.
Once the analysis is underway, an X–Y plot of the values of the degree of freedom that you selected to monitor (the punch's vertical displacement) appears in a separate viewport. From the main menu bar, select to follow the progression of the punch's displacement in the 2-direction over time as the analysis runs.
-