Axisymmetric solid element library

This section provides a reference to the axisymmetric solid elements available in Abaqus/Standard and Abaqus/Explicit.

Related Topics
Solid (continuum) elements
In Other Guides
*SOLID SECTION

ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE

Conventions

Coordinate 1 is r, coordinate 2 is z. At θ=0 the r-direction corresponds to the global x-direction and the z-direction corresponds to the global y-direction. This is important when data must be given in global directions. Coordinate 1 must be greater than or equal to zero.

Degree of freedom 1 is ur, degree of freedom 2 is uz. Generalized axisymmetric elements with twist have an additional degree of freedom, 5, corresponding to the twist angle ϕ (in radians).

Abaqus does not automatically apply any boundary conditions to nodes located along the symmetry axis. You must apply radial or symmetry boundary conditions on these nodes if desired.

In certain situations in Abaqus/Standard it may become necessary to apply radial boundary conditions on nodes that are located on the symmetry axis to obtain convergence in nonlinear problems. Therefore, the application of radial boundary conditions on nodes on the symmetry axis is recommended for nonlinear problems.

Point loads and moments, concentrated (nodal) fluxes, electrical currents, and seepage should be given as the value integrated around the circumference (that is, the total value on the ring).

Element types

Stress/displacement elements without twist

CAX3

3-node linear

CAX3H(S)

3-node linear, hybrid with constant pressure

CAX4(S)

4-node bilinear

CAX4H(S)

4-node bilinear, hybrid with constant pressure

CAX4I(S)

4-node bilinear, incompatible modes

CAX4IH(S)

4-node bilinear, incompatible modes, hybrid with linear pressure

CAX4R

4-node bilinear, reduced integration with hourglass control

CAX4RH(S)

4-node bilinear, reduced integration with hourglass control, hybrid with constant pressure

CAX6(S)

6-node quadratic

CAX6H(S)

6-node quadratic, hybrid with linear pressure

CAX6M

6-node modified, with hourglass control

CAX6MH(S)

6-node modified, with hourglass control, hybrid with linear pressure

CAX8(S)

8-node biquadratic

CAX8H(S)

8-node biquadratic, hybrid with linear pressure

CAX8R(S)

8-node biquadratic, reduced integration

CAX8RH(S)

8-node biquadratic, reduced integration, hybrid with linear pressure

Active degrees of freedom

1, 2

Additional solution variables

The constant pressure hybrid elements have one additional variable and the linear pressure elements have three additional variables relating to pressure.

Element types CAX4I and CAX4IH have five additional variables relating to the incompatible modes.

Element types CAX6M and CAX6MH have two additional displacement variables.

Stress/displacement elements with twist

CGAX3(S)

3-node linear

CGAX3H(S)

3-node linear, hybrid with constant pressure

CGAX4(S)

4-node bilinear

CGAX4H(S)

4-node bilinear, hybrid with constant pressure

CGAX4R(S)

4-node bilinear, reduced integration with hourglass control

CGAX4RH(S)

4-node bilinear, reduced integration with hourglass control, hybrid with constant pressure

CGAX6(S)

6-node quadratic

CGAX6H(S)

6-node quadratic, hybrid with linear pressure

CGAX6M(S)

6-node modified, with hourglass control

CGAX6MH(S)

6-node modified, with hourglass control, hybrid with linear pressure

CGAX8(S)

8-node biquadratic

CGAX8H(S)

8-node biquadratic, hybrid with linear pressure

CGAX8R(S)

8-node biquadratic, reduced integration

CGAX8RH(S)

8-node biquadratic, reduced integration, hybrid with linear pressure

Active degrees of freedom

1, 2, 5

Additional solution variables

The constant pressure hybrid elements have one additional variable and the linear pressure elements have three additional variables relating to pressure.

Element types CGAX6M and CGAX6MH have three additional displacement variables.

Diffusive heat transfer or mass diffusion elements

DCAX3(S)

3-node linear

DCAX4(S)

4-node linear

DCAX6(S)

6-node quadratic

DCAX8(S)

8-node quadratic

Active degrees of freedom

11

Additional solution variables

None.

Forced convection/diffusion elements

DCCAX2(S)

2-node

DCCAX2D(S)

2-node with dispersion control

DCCAX4(S)

4-node

DCCAX4D(S)

4-node with dispersion control

Active degrees of freedom

11

Additional solution variables

None.

Coupled thermal-electrical elements

DCAX3E(S)

3-node linear

DCAX4E(S)

4-node linear

DCAX6E(S)

6-node quadratic

DCAX8E(S)

8-node quadratic

Active degrees of freedom

9, 11

Additional solution variables

None.

Coupled temperature-displacement elements without twist

CAX3T

3-node linear displacement and temperature

CAX4T(S)

4-node bilinear displacement and temperature

CAX4HT(S)

4-node bilinear displacement and temperature, hybrid with constant pressure

CAX4RT

4-node bilinear displacement and temperature, reduced integration with hourglass control

CAX4RHT(S)

4-node bilinear displacement and temperature, reduced integration with hourglass control, hybrid with constant pressure

CAX6MT

6-node modified displacement and temperature, with hourglass control

CAX6MHT(S)

6-node modified displacement and temperature, with hourglass control, hybrid with linear pressure

CAX8T(S)

8-node biquadratic displacement, bilinear temperature

CAX8HT(S)

8-node biquadratic displacement, bilinear temperature, hybrid with linear pressure

CAX8RT(S)

8-node biquadratic displacement, bilinear temperature, reduced integration

CAX8RHT(S)

8-node biquadratic displacement, bilinear temperature, reduced integration, hybrid with linear pressure

Active degrees of freedom

1, 2, 11 at corner nodes

1, 2 at midside nodes of second-order elements in Abaqus/Standard

1, 2, 11 at midside nodes of the modified displacement and temperature elements in Abaqus/Standard

Additional solution variables

The constant pressure hybrid elements have one additional variable and the linear pressure elements have three additional variables relating to pressure.

Element types CAX6MT and CAX6MHT have two additional displacement variables and one additional temperature variable.

Coupled temperature-displacement elements with twist

CGAX3T(S)

3-node linear displacement and temperature

CGAX3HT(S)

3-node linear displacement and temperature, hybrid with constant pressure

CGAX4T(S)

4-node bilinear displacement and temperature

CGAX4HT(S)

4-node bilinear displacement and temperature, hybrid with constant pressure

CGAX4RT(S)

4-node bilinear displacement and temperature, reduced integration with hourglass control

CGAX4RHT(S)

4-node bilinear displacement and temperature, reduced integration with hourglass control, hybrid with constant pressure

CGAX6MT(S)

6-node modified displacement and temperature, with hourglass control

CGAX6MHT(S)

6-node modified displacement and temperature, with hourglass control, hybrid with constant pressure

CGAX8T(S)

8-node biquadratic displacement, bilinear temperature

CGAX8HT(S)

8-node biquadratic displacement, bilinear temperature, hybrid with linear pressure

CGAX8RT(S)

8-node biquadratic displacement, bilinear temperature, reduced integration

CGAX8RHT(S)

8-node biquadratic displacement, bilinear temperature, reduced integration, hybrid with linear pressure

Active degrees of freedom

1, 2, 5, 11 at corner nodes

1, 2, 5 at midside nodes of second-order elements

1, 2, 5, 11 at midside nodes of the modified displacement and temperature elements

Additional solution variables

The constant pressure hybrid elements have one additional variable and the linear pressure elements have three additional variables relating to pressure.

Element types CGAX6MT and CGAX6MHT have two additional displacement variables and one additional temperature variable.

Pore pressure elements

CAX4P(S)

4-node bilinear displacement and pore pressure

CAX4PH(S)

4-node bilinear displacement and pore pressure, hybrid with constant pressure

CAX4RP(S)

4-node bilinear displacement and pore pressure, reduced integration with hourglass control

CAX4RPH(S)

4-node bilinear displacement and pore pressure, reduced integration with hourglass control, hybrid with constant pressure

CAX6MP(S)

6-node modified displacement and pore pressure, with hourglass control

CAX6MPH(S)

6-node modified displacement and pore pressure, with hourglass control, hybrid with linear pressure

CAX8P(S)

8-node biquadratic displacement, bilinear pore pressure

CAX8PH(S)

8-node biquadratic displacement, bilinear pore pressure, hybrid with linear pressure

CAX8RP(S)

8-node biquadratic displacement, bilinear pore pressure, reduced integration

CAX8RPH(S)

8-node biquadratic displacement, bilinear pore pressure, reduced integration, hybrid with linear pressure

Active degrees of freedom

1, 2, 8 at corner nodes

1, 2 at midside nodes

Additional solution variables

The constant pressure hybrid elements have one additional variable relating to the effective pressure stress, and the linear pressure hybrid elements have three additional variables relating to the effective pressure stress to permit fully incompressible material modeling.

Element types CAX6MP and CAX6MPH have two additional displacement variables and one additional pore pressure variable.

Coupled temperature–pore pressure elements

CAX4PT(S)

4-node bilinear displacement, pore pressure, and temperature

CAX4RPT(S)

4-node bilinear displacement, pore pressure, and temperature; reduced integration with hourglass control

CAX4RPHT(S)

4-node bilinear displacement, pore pressure, and temperature; reduced integration with hourglass control, hybrid with constant pressure

Active degrees of freedom

1, 2, 8, 11

Additional solution variables

The constant pressure hybrid elements have one additional variable relating to the effective pressure stress to permit fully incompressible material modeling.

Acoustic elements

ACAX3

3-node linear

ACAX4R(E)

4-node linear, reduced integration with hourglass control

ACAX4(S)

4-node linear

ACAX6(S)

6-node quadratic

ACAX8(S)

8-node quadratic

Active degrees of freedom

8

Additional solution variables

None.

Piezoelectric elements

CAX3E(S)

3-node linear

CAX4E(S)

4-node bilinear

CAX6E(S)

6-node quadratic

CAX8E(S)

8-node biquadratic

CAX8RE(S)

8-node biquadratic, reduced integration

Active degrees of freedom

1, 2, 9

Additional solution variables

None.

Nodal coordinates required

r, z at θ=0

Element property definition

For element types DCCAX2 and DCCAX2D, you must specify the channel thickness of the element in the (r–z) plane. The default is unit thickness if no thickness is given.

For all other elements, you do not need to specify the thickness.

Input File Usage

SOLID SECTION

Abaqus/CAE Usage

Property module: Create Section: select Solid as the section Category and Homogeneous as the section Type

Element-based loading

Distributed loads

Distributed loads are available for all elements with displacement degrees of freedom. They are specified as described in Distributed loads. Distributed load magnitudes are per unit area or per unit volume. They do not need to be multiplied by 2⁢π.

*dload
  1. Load ID (*DLOAD): BR
  2. Body force
  3. FL−3

  4. Body force in radial direction.

  1. Load ID (*DLOAD): BZ
  2. Body force
  3. FL−3

  4. Body force in axial direction.

  1. Load ID (*DLOAD): BRNU
  2. Body force
  3. FL−3

  4. Nonuniform body force in radial direction with magnitude supplied via user subroutine DLOAD in Abaqus/Standard and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DLOAD): BZNU
  2. Body force
  3. FL−3

  4. Nonuniform body force in axial direction with magnitude supplied via user subroutine DLOAD in Abaqus/Standard and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DLOAD): CENT(S)
  2. Not supported
  3. FL−4M−3T−2

  4. Centrifugal load (magnitude input as ρ⁢ω2, where ρ is the mass density per unit volume, ω is the angular velocity). Not available for pore pressure elements.

  1. Load ID (*DLOAD): CENTRIF(S)
  2. Rotational body force
  3. T−2

  4. Centrifugal load (magnitude is input as ω2, where ω is the angular velocity).

  1. Load ID (*DLOAD): GRAV
  2. Gravity
  3. LT−2

  4. Gravity loading in a specified direction (magnitude is input as acceleration).

  1. Load ID (*DLOAD): HPn(S)
  2. Not supported
  3. FL−2

  4. Hydrostatic pressure on face n, linear in global Y.

  1. Load ID (*DLOAD): Pn
  2. Pressure
  3. FL−2

  4. Pressure on face n.

  1. Load ID (*DLOAD): PnNU
  2. Not supported
  3. FL−2

  4. Nonuniform pressure on face n with magnitude supplied via user subroutine DLOAD in Abaqus/Standard and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DLOAD): SBF(E)
  2. Not supported
  3. FL−5T2

  4. Stagnation body force in radial and axial directions.

  1. Load ID (*DLOAD): SPn(E)
  2. Not supported
  3. FL−4T2

  4. Stagnation pressure on face n.

  1. Load ID (*DLOAD): TRSHRn
  2. Surface traction
  3. FL−2

  4. Shear traction on face n.

  1. Load ID (*DLOAD): TRSHRnNU(S)
  2. Not supported
  3. FL−2

  4. Nonuniform shear traction on face n with magnitude and direction supplied via user subroutine UTRACLOAD.

  1. Load ID (*DLOAD): TRVECn
  2. Surface traction
  3. FL−2

  4. General traction on face n.

  1. Load ID (*DLOAD): TRVECnNU(S)
  2. Not supported
  3. FL−2

  4. Nonuniform general traction on face n with magnitude and direction supplied via user subroutine UTRACLOAD.

  1. Load ID (*DLOAD): VBF(E)
  2. Not supported
  3. FL−4T

  4. Viscous body force in radial and axial directions.

  1. Load ID (*DLOAD): VPn(E)
  2. Not supported
  3. FL−3T

  4. Viscous pressure on face n, applying a pressure proportional to the velocity normal to the face and opposing the motion.

Foundations

Foundations are available for Abaqus/Standard elements with displacement degrees of freedom. They are specified as described in Element foundations.

*foundation
  1. Load ID (*FOUNDATION): Fn(S)
  2. Elastic foundation
  3. FL−3

  4. Elastic foundation on face n. For CGAX elements the elastic foundations are applied to degrees of freedom ur and uz only.

Distributed heat fluxes

Distributed heat fluxes are available for all elements with temperature degrees of freedom. They are specified as described in Thermal loads. Distributed heat flux magnitudes are per unit area or per unit volume. They do not need to be multiplied by 2⁢π.

*dflux
  1. Load ID (*DFLUX): BF
  2. Body heat flux
  3. JL−3T−1

  4. Heat body flux per unit volume.

  1. Load ID (*DFLUX): BFNU
  2. Body heat flux
  3. JL−3T−1

  4. Nonuniform heat body flux per unit volume with magnitude supplied via user subroutine DFLUX in Abaqus/Standard and VDFLUX in Abaqus/Explicit.

  1. Load ID (*DFLUX): Sn
  2. Surface heat flux
  3. JL−2T−1

  4. Heat surface flux per unit area into face n.

  1. Load ID (*DFLUX): SnNU
  2. Not supported
  3. JL−2T−1

  4. Nonuniform heat surface flux per unit area into face n with magnitude supplied via user subroutine DFLUX in Abaqus/Standard and VDFLUX in Abaqus/Explicit.

Film conditions

Film conditions are available for all elements with temperature degrees of freedom. They are specified as described in Thermal loads.

*film
  1. Load ID (*FILM): Fn
  2. Surface film condition
  3. JL−2T−1θ−1

  4. Film coefficient and sink temperature (units of θ) provided on face n.

  1. Load ID (*FILM): FnNU(S)
  2. Not supported
  3. JL−2T−1θ−1

  4. Nonuniform film coefficient and sink temperature (units of θ) provided on face n with magnitude supplied via user subroutine FILM.

Radiation types

Radiation conditions are available for all elements with temperature degrees of freedom. They are specified as described in Thermal loads.

*radiate
  1. Load ID (*RADIATE): Rn
  2. Surface radiation
  3. Dimensionless

  4. Emissivity and sink temperature provided for face n.

Distributed flows

Distributed flows are available for all elements with pore pressure degrees of freedom. They are specified as described in Pore fluid flow. Distributed flow magnitudes are per unit area or per unit volume. They do not need to be multiplied by 2⁢π.

*flow
  1. Load ID (*FLOW): Qn(S)
  2. Not supported
  3. F−1L3T−1

  4. Seepage coefficient and reference sink pore pressure (units of FL−2) provided on face n.

  1. Load ID (*FLOW): QnD(S)
  2. Not supported
  3. F−1L3T−1

  4. Drainage-only seepage coefficient provided on face n.

  1. Load ID (*FLOW): QnNU(S)
  2. Not supported
  3. F−1L3T−1

  4. Nonuniform seepage coefficient and reference sink pore pressure (units of FL−2) provided on face n with magnitude supplied via user subroutine FLOW.

*dflow
  1. Load ID (*DFLOW): Sn(S)
  2. Surface pore fluid
  3. LT−1

  4. Prescribed pore fluid effective velocity (outward from the face) on face n.

  1. Load ID (*DFLOW): SnNU(S)
  2. Not supported
  3. LT−1

  4. Nonuniform prescribed pore fluid effective velocity (outward from the face) on face n with magnitude supplied via user subroutine DFLOW.

Distributed impedances

Distributed impedances are available for all elements with acoustic pressure degrees of freedom. They are specified as described in Acoustic and shock loads.

*impedance
  1. Load ID (*IMPEDANCE): In
  2. Not supported
  3. None

  4. Name of the impedance property that defines the impedance on face n.

Electric fluxes

Electric fluxes are available for piezoelectric elements. They are specified as described in Piezoelectric analysis.

*decharge
  1. Load ID (*DECHARGE): EBF(S)
  2. Body charge
  3. CL−3

  4. Body flux per unit volume.

  1. Load ID (*DECHARGE): ESn(S)
  2. Surface charge
  3. CL−2

  4. Prescribed surface charge on face n.

Distributed electric current densities

Distributed electric current densities are available for coupled thermal-electrical elements. They are specified as described in Coupled thermal-electrical analysis.

*decurrent
  1. Load ID (*DECURRENT): CBF(S)
  2. Body current
  3. CL−3T−1

  4. Volumetric current source density.

  1. Load ID (*DECURRENT): CSn(S)
  2. Surface current
  3. CL−2T−1

  4. Current density on face n.

Distributed concentration fluxes

Distributed concentration fluxes are available for mass diffusion elements. They are specified as described in Mass diffusion analysis.

*dflux
  1. Load ID (*DFLUX): BF(S)
  2. Body concentration flux
  3. PT−1

  4. Concentration body flux per unit volume.

  1. Load ID (*DFLUX): BFNU(S)
  2. Body concentration flux
  3. PT−1

  4. Nonuniform concentration body flux per unit volume with magnitude supplied via user subroutine DFLUX.

  1. Load ID (*DFLUX): Sn(S)
  2. Surface concentration flux
  3. PLT−1

  4. Concentration surface flux per unit area into face n.

  1. Load ID (*DFLUX): SnNU(S)
  2. Surface concentration flux
  3. PLT−1

  4. Nonuniform concentration surface flux per unit area into face n with magnitude supplied via user subroutine DFLUX.

Surface-based loading

Distributed loads

Surface-based distributed loads are available for all elements with displacement degrees of freedom. They are specified as described in Distributed loads. Distributed load magnitudes are per unit area or per unit volume. They do not need to be multiplied by 2⁢π.

*dsload
  1. Load ID (*DSLOAD): HP(S)
  2. Pressure
  3. FL−2

  4. Hydrostatic pressure on the element surface, linear in global Y.

  1. Load ID (*DSLOAD): P
  2. Pressure
  3. FL−2

  4. Pressure on the element surface.

  1. Load ID (*DSLOAD): PNU
  2. Pressure
  3. FL−2

  4. Nonuniform pressure on the element surface with magnitude supplied via user subroutine DLOAD in Abaqus/Standard and VDLOAD in Abaqus/Explicit.

  1. Load ID (*DSLOAD): SP(E)
  2. Pressure
  3. FL−4T2

  4. Stagnation pressure on the element surface.

  1. Load ID (*DSLOAD): TRSHR
  2. Surface traction
  3. FL−2

  4. Shear traction on the element surface.

  1. Load ID (*DSLOAD): TRSHRNU(S)
  2. Surface traction
  3. FL−2

  4. Nonuniform shear traction on the element surface with magnitude and direction supplied via user subroutine UTRACLOAD.

  1. Load ID (*DSLOAD): TRVEC
  2. Surface traction
  3. FL−2

  4. General traction on the element surface.

  1. Load ID (*DSLOAD): TRVECNU(S)
  2. Surface traction
  3. FL−2

  4. Nonuniform general traction on the element surface with magnitude and direction supplied via user subroutine UTRACLOAD.

  1. Load ID (*DSLOAD): VP(E)
  2. Pressure
  3. FL−3T

  4. Viscous pressure applied on the element surface. The viscous pressure is proportional to the velocity normal to the face and opposing the motion.

Distributed heat fluxes

Surface-based heat fluxes are available for all elements with temperature degrees of freedom. They are specified as described in Thermal loads. Distributed heat flux magnitudes are per unit area or per unit volume. They do not need to be multiplied by 2⁢π.

*dsflux
  1. Load ID (*DSFLUX): S
  2. Surface heat flux
  3. JL−2T−1

  4. Heat surface flux per unit area into the element surface.

  1. Load ID (*DSFLUX): SNU
  2. Surface heat flux
  3. JL−2T−1

  4. Nonuniform heat surface flux per unit area into the element surface with magnitude supplied via user subroutine DFLUX in Abaqus/Standard and VDFLUX in Abaqus/Explicit.

Film conditions

Surface-based film conditions are available for all elements with temperature degrees of freedom. They are specified as described in Thermal loads.

*sfilm
  1. Load ID (*SFILM): F
  2. Surface film condition
  3. JL−2T−1θ−1

  4. Film coefficient and sink temperature (units of θ) provided on the element surface.

  1. Load ID (*SFILM): FNU(S)
  2. Surface film condition
  3. JL−2T−1θ−1

  4. Nonuniform film coefficient and sink temperature (units of θ) provided on the element surface with magnitude supplied via user subroutine FILM.

Radiation types

Surface-based radiation conditions are available for all elements with temperature degrees of freedom. They are specified as described in Thermal loads.

*sradiate
  1. Load ID (*SRADIATE): R
  2. Surface radiation
  3. Dimensionless

  4. Emissivity and sink temperature provided for the element surface.

Distributed flows

Surface-based distributed flows are available for all elements with pore pressure degrees of freedom. They are specified as described in Pore fluid flow. Distributed flow magnitudes are per unit area or per unit volume. They do not need to be multiplied by 2⁢π.

*sflow
  1. Load ID (*SFLOW): Q(S)
  2. Not supported
  3. F−1L3T−1

  4. Seepage coefficient and reference sink pore pressure (units of FL−2) provided on the element surface.

  1. Load ID (*SFLOW): QD(S)
  2. Not supported
  3. F−1L3T−1

  4. Drainage-only seepage coefficient provided on the element surface.

  1. Load ID (*SFLOW): QNU(S)
  2. Not supported
  3. F−1L3T−1

  4. Nonuniform seepage coefficient and reference sink pore pressure (units of FL−2) provided on the element surface with magnitude supplied via user subroutine FLOW.

*dsflow
  1. Load ID (*DSFLOW): S(S)
  2. Surface pore fluid
  3. LT−1

  4. Prescribed pore fluid effective velocity outward from the element surface.

  1. Load ID (*DSFLOW): SNU(S)
  2. Surface pore fluid
  3. LT−1

  4. Nonuniform prescribed pore fluid effective velocity outward from the element surface with magnitude supplied via user subroutine DFLOW.

Distributed impedances

Surface-based impedances are available for all elements with acoustic pressure degrees of freedom. They are specified as described in Acoustic and shock loads.

Incident wave loading

Surface-based incident wave loads are available for all elements with displacement degrees of freedom or acoustic pressure degrees of freedom. They are specified as described in Acoustic and shock loads. If the incident wave field includes a reflection off a plane outside the boundaries of the mesh, this effect can be included.

Electric fluxes

Surface-based electric fluxes are available for piezoelectric elements. They are specified as described in Piezoelectric analysis.

*dsecharge
  1. Load ID (*DSECHARGE): ES(S)
  2. Surface charge
  3. CL−2

  4. Prescribed surface charge on the element surface.

Distributed electric current densities

Surface-based electric current densities are available for coupled thermal-electrical elements. They are specified as described in Coupled thermal-electrical analysis.

*dsecurrent
  1. Load ID (*DSECURRENT): CS(S)
  2. Surface current
  3. CL−2T−1

  4. Current density on the element surface.

Element output

Output is in global directions unless a local coordinate system is assigned to the element through the section definition (Orientations) in which case output is in the local coordinate system (which rotates with the motion in large-displacement analysis). See State storage for details. For regular axisymmetric elements, the local orientation must be in the r–z plane with θ being a principal direction. For generalized axisymmetric elements with twist, the local orientation can be arbitrary.

Stress, strain, and other tensor components

Stress and other tensors (including strain tensors) are available for elements with displacement degrees of freedom. All tensors have the same components. For example, the stress components are as follows:

For elements with displacement degrees of freedom without twist:

S11

Stress in the radial direction or in the local 1-direction.

S22

Stress in the axial direction or in the local 2-direction.

S33

Hoop direct stress.

S12

Shear stress.

For elements with displacement degrees of freedom with twist:

S11

Stress in the radial direction or in the local 1-direction.

S22

Stress in the axial direction or in the local 2-direction.

S33

Stress in the circumferential direction or in the local 3-direction.

S12

Shear stress.

S13

Shear stress.

S23

Shear stress.

Heat flux components

Available for elements with temperature degrees of freedom.

HFL1

Heat flux in the radial direction or in the local 1-direction.

HFL2

Heat flux in the axial direction or in the local 2-direction.

Pore fluid velocity components

Available for elements with pore pressure degrees of freedom, except for acoustic elements.

FLVEL1

Pore fluid effective velocity in the radial direction or in the local 1-direction.

FLVEL2

Pore fluid effective velocity in the axial direction or in the local 2-direction.

Mass concentration flux components

Available for elements with normalized concentration degrees of freedom.

MFL1

Concentration flux in the radial direction or in the local 1-direction.

MFL2

Concentration flux in the axial direction or in the local 2-direction.

Electrical potential gradient

Available for elements with electrical potential degrees of freedom.

EPG1

Electrical potential gradient in the 1-direction.

EPG2

Electrical potential gradient in the 2-direction.

Electrical flux components

Available for piezoelectric elements.

EFLX1

Electrical flux in the 1-direction.

EFLX2

Electrical flux in the 2-direction.

Electrical current density components

Available for coupled thermal-electrical elements.

ECD1

Electrical current density in the 1-direction.

ECD2

Electrical current density in the 2-direction.

Node ordering and face numbering on elements



Table 1. 2-node element faces
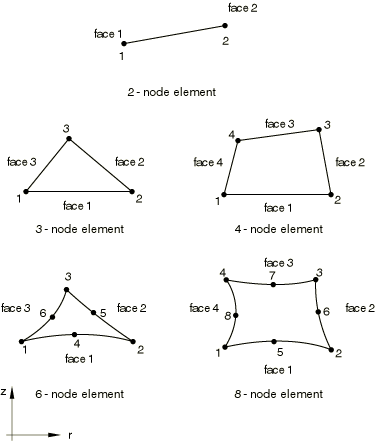
Face 1 Section at node 1
Face 2 Section at node 2
Table 2. Triangular element faces
Face 1 1 – 2 face
Face 2 2 – 3 face
Face 3 3 – 1 face
Table 3. Quadrilateral element faces
Face 1 1 – 2 face
Face 2 2 – 3 face
Face 3 3 – 4 face
Face 4 4 – 1 face

Numbering of integration points for output



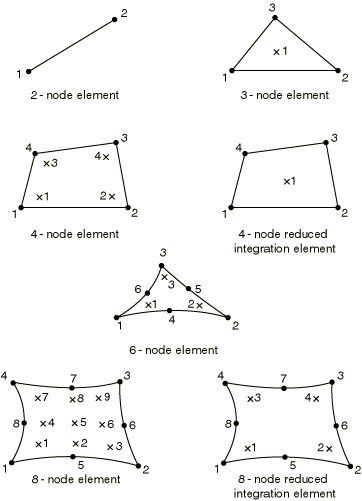
For heat transfer applications a different integration scheme is used for triangular elements, as described in Triangular, tetrahedral, and wedge elements.