Dashpots | ||||||||
|
| |||||||
ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE
Typical Applications
Dashpots are used to model relative velocity-dependent force or torsional resistance. They can also provide viscous energy dissipation mechanisms.
Dashpots are often useful in unstable, nonlinear, static analyses where the modified Riks algorithm is not appropriate (see Unstable collapse and postbuckling analysis for a discussion of the modified Riks algorithm) and where the automatic time stepping algorithm is used because sudden shifts in configuration can be controlled by the forces that arise in the dashpots. In such cases the magnitude of the damping must be chosen in conjunction with the time period so that enough damping is available to control such difficulties but the damping forces are negligible when a stable static response is obtained. See also the contact damping available with contact elements in Abaqus/Standard (see Contact damping).
![]()
Choosing an appropriate element
DASHPOT1 and DASHPOT2 elements are available only in Abaqus/Standard. DASHPOT1 is between a specified degree of freedom and ground. DASHPOT2 is between two specified degrees of freedom.
The DASHPOTA element is available in both Abaqus/Standard and Abaqus/Explicit. DASHPOTA is between two nodes with its line of action being the line joining the two nodes.
The dashpot behavior can be linear or nonlinear in any of these elements.
Input File Usage
Use the following option to specify a dashpot element between a specified degree of freedom and ground:
ELEMENT, TYPE=DASHPOT1
Use the following option to specify a dashpot element between two degrees of freedom:
ELEMENT, TYPE=DASHPOT2
Use the following option to specify a dashpot element between two nodes with its line of action being the line joining the two nodes:
ELEMENT, TYPE=DASHPOTA
Abaqus/CAE Usage
Property or Interaction module: , then select one of the following: Connect points to ground: select points: toggle on Dashpot coefficient (equivalent to DASHPOT1) Connect two points: select points: Axis: Specify fixed direction: toggle on Dashpot coefficient (equivalent to DASHPOT2) Connect two points: select points: Axis: Follow line of action: toggle on Dashpot coefficient (equivalent to DASHPOTA)
![]()
Stability considerations in Abaqus/Explicit
Abaqus/Explicit does not take dashpots into account when determining the stable time step; therefore, care should be taken when introducing dashpots into the mesh.
A DASHPOTA element introduces a damping force between two degrees of freedom without introducing any stiffness between these degrees of freedom and without introducing any mass at the nodes. This can cause a reduction in the stable time increment. For example, consider a simple system of a truss element and a dashpot element as shown in Figure 1.
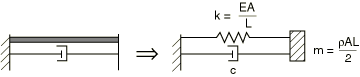
The dynamic equation for this system is
or
where
and
The stable time increment for the spring-dashpot system is
As the dashpot coefficient c is increased, the stable time increment, , will be reduced.
To avoid this reduction in the stable time increment, dashpots should be used in parallel with spring or truss elements, where the stiffness of the spring or truss elements is chosen so that the stable time increment of the dashpot and spring or truss is larger than the stable critical time increment that is calculated by Abaqus/Explicit. If this requires springs or trusses that have unacceptable forces, specify the time increment size directly for the step (see Explicit dynamic analysis).
![]()
Relative velocity definition
The relative velocity definition depends on the element type.
DASHPOT1 elements
The relative velocity across a DASHPOT1 element is the ith component of velocity of the dashpot's node:
where i is defined as described below and can be in a local direction (see Defining the direction of action for DASHPOT1 and DASHPOT2 elements).
DASHPOT2 elements
The relative velocity across a DASHPOT2 element is the difference between the ith component of velocity at the dashpot's first node and the jth component of velocity of the dashpot's second node:
where i and j are defined as described below and can be in local directions (see Defining the direction of action for DASHPOT1 and DASHPOT2 elements).
It is important to understand how the DASHPOT2 element will behave according to the above relative displacement
equation since the element can produce counterintuitive results. For example, a
DASHPOT2 element set up in the following way will be a “compressive”
dashpot:
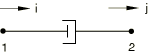
If the nodes have velocities such that
and ,
the dashpot is compressed while the force in the dashpot is positive. To obtain
a “tensile” dashpot, the DASHPOT2 element should be set up in the following way:
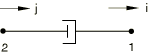
DASHPOTA elements
The relative velocity across a DASHPOTA element is the difference between the velocity of the dashpot's second node and the dashpot's first node, taken in the direction of the current axis of the dashpot.
For geometrically linear analysis,
where is the reference position of the dashpot's first node, is the reference position of the dashpot's second node, and is the reference length of the dashpot.
For geometrically nonlinear analysis,
where is the current position of the dashpot's first node, is the current position of the dashpot's second node, and l is the current length of the dashpot.
In either case the force in a DASHPOTA element is positive if the dashpot is extending.
![]()
Defining dashpot behavior
The dashpot behavior can be linear or nonlinear. In either case you must associate the dashpot behavior with a region of your model.
Abaqus/CAE Usage
Property or Interaction module: : select connectivity type: select pointsLinear dashpot behavior
You define linear dashpot behavior by specifying a constant dashpot coefficient (force per relative velocity).
The dashpot coefficient can depend on temperature and field variables. See Input Syntax Rules for further information about defining data as functions of temperature and independent field variables.
For direct-solution steady-state dynamic analysis the dashpot coefficient can depend on frequency, as well as on temperature and field variables. If a frequency-dependent dashpot coefficient is specified for any other analysis procedure in Abaqus/Standard, the data for the lowest frequency given will be used.
Input File Usage
DASHPOT, DEPENDENCIES=n first data line dashpot coefficient, frequency, temperature, field variable 1, etc. ...
Abaqus/CAE Usage
Property or Interaction module: : select connectivity type: select points: Property: Dashpot coefficient: dashpot coefficient
Defining the dashpot coefficient as a function of frequency, temperature, and field variables is not supported in Abaqus/CAE when you define dashpots as engineering features; instead, you can define connectors that have dashpot-like damping behavior (see Connector damping behavior).
Nonlinear dashpot behavior
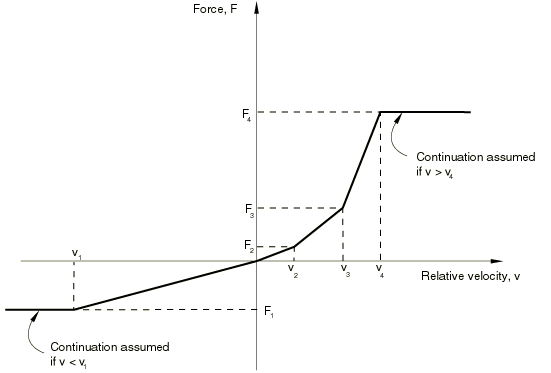
You define nonlinear dashpot behavior by giving pairs of force–relative velocity values. These values should be given in ascending order of relative velocity and should be provided over a sufficiently wide range of relative velocity values so that the behavior is defined correctly. Abaqus assumes that the force remains constant outside the range given (see Figure 2). In addition, the curve should pass through the origin. That is, the force should be zero at zero relative velocity.
The dashpot coefficient can depend on temperature and field variables. See Input Syntax Rules for further information about defining data as functions of temperature and independent field variables.
Abaqus/Explicit will regularize the data into tables that are defined in terms of even intervals of the independent variables. In some cases where the force is defined at uneven intervals of the independent variable (relative velocity) and the range of the independent variable is large compared to the smallest interval, Abaqus/Explicit may fail to obtain an accurate regularization of your data in a reasonable number of intervals. In this case the program will stop after all data are processed with an error message that you must redefine the material data. See Material data definition for a more detailed discussion of data regularization.
Input File Usage
DASHPOT, NONLINEAR, DEPENDENCIES=n first data line force, relative velocity, temperature, field variable 1, etc. ...
Abaqus/CAE Usage
Defining nonlinear dashpot behavior is not supported in Abaqus/CAE when you define dashpots as engineering features; instead, you can define connectors that have dashpot-like damping behavior (see Connector damping behavior).
![]()
Defining the direction of action for DASHPOT1 and DASHPOT2 elements
You define the direction of action for DASHPOT1 and DASHPOT2 elements by giving the degree of freedom at each node of the element. This degree of freedom may be in a local coordinate system (Orientations). This local system is assumed to be fixed: even in large-displacement analysis DASHPOT1 and DASHPOT2 elements act in a fixed direction throughout the analysis.
Input File Usage
DASHPOT, ORIENTATION=name dof at node 1, dof at node 2
Abaqus/CAE Usage
Property or Interaction module: , then select one of the following: Connect points to ground: select points: Orientation: : select orientation Connect two points: select points: Axis: Specify fixed direction: Orientation: : select orientation
![]()
Dashpots within substructures
Dashpots cannot be used within substructures. You can define Rayleigh damping within the substructure definition or on the usage level to create damping within a substructure; see Defining substructure damping for more information.