Linear analysis of a rod under dynamic loading | ||||||
|
| |||||
ProductsAbaqus/Standard
Problem description
The model consists of three truss elements of type T3D2 located along the x-axis, with the y- and z-displacement components restrained, so the problem is one-dimensional. The x-displacement at node 1 is also restrained, leaving three active degrees of freedom. The structure has a total length of 30, cross-sectional area of 2, density of 1/90, and Young's modulus of 5. (All values are given in consistent units.)
![]()
Eigenvalue calculations
The first step for all of the linear dynamics procedures is to calculate the eigenvalues and eigenvectors of the system. The mass matrix of element type T3D2 is lumped; therefore, the mass matrix of this three truss system is
The stiffness matrix of the system is
The three eigenvalues and the corresponding eigenvectors using the default normalization method are given in the following table:
| Mode | Eigenvalue | Frequency | Eigenvector magnitude at node | |||
|---|---|---|---|---|---|---|
| (Hz) | 1 | 2 | 3 | 4 | ||
| 1 | 1.2058 | 0.1748 | 0 | 0.5 | 0.866 | 1.0 |
| 2 | 9.0 | 0.4775 | 0 | 1.0 | 0 | −1.0 |
| 3 | 16.794 | 0.6522 | 0 | 0.5 | −0.866 | 1.0 |
Abaqus also calculates the modal participation factors, , the generalized mass, , and the effective mass for each eigenvector (see Variables associated with the natural modes of a model for definitions). The values in this case are:
| Mode | Participation | Generalized | Effective |
|---|---|---|---|
| factor | mass | mass | |
| 1 | 1.244 | 0.333 | 0.5158 |
| 2 | 0.333 | 0.333 | 0.0370 |
| 3 | 0.0893 | 0.333 | 0.00266 |
Alternate normalization
Abaqus allows the eigenvectors to be normalized in one of two ways: such that the largest displacement entry in each eigenvector is unity (default) or such that the generalized mass for each eigenvector is unity. Normalization of eigenvectors is discussed in Natural frequency extraction. In general, if the default normalization is requested the signs of the eigenvectors obtained using different eigenvalue extraction methods or different platforms are consistent because the largest displacement entry in each eigenvector is scaled to positive unity. For this type of normalization the signs of the eigenvector entries may differ for different methods and different platforms only in the case that the maximum and minimum displacement entries in an eigenvector are of equal magnitude but opposite sign. On the other hand, if mass normalization is requested, the signs of the eigenvectors obtained using different methods or different platforms may vary because, in this case, the eigenvectors are scaled by positive values. The values and signs of the modal participation factors depend on the normalization type and signs of corresponding eigenvectors.
Generalized coordinates for modal dynamic, response spectrum, steady-state, and random response analyses are different depending on the eigenvector normalization. Consequently, for mass normalization the signs of generalized coordinates will change depending on the signs of the eigenvectors. However, the physical values calculated using the summation of the modal values are independent of the eigenvector normalization.
For this example, the corresponding values using mass normalization are given in the following tables:
| Mode | Eigenvalue | Frequency | Eigenvector magnitude at node | |||
|---|---|---|---|---|---|---|
| (Hz) | 1 | 2 | 3 | 4 | ||
| 1 | 1.2058 | 0.1748 | 0 | 0.866 | 1.5 | 1.732 |
| 2 | 9.0 | 0.4775 | 0 | −1.732 | 0 | 1.732 |
| 3 | 16.794 | 0.6522 | 0 | −0.866 | 1.5 | −1.732 |
| Mode | Participation | Generalized | Effective |
|---|---|---|---|
| factor | mass | mass | |
| 1 | 0.718 | 1.0 | 0.5158 |
| 2 | −0.192 | 1.0 | 0.0370 |
| 3 | −0.0516 | 1.0 | 0.00266 |
![]()
Modal dynamic analysis
This analysis is performed for three types of systems, described below.
Tip load—damped system
The time history response is obtained for the system when a load of 10 is applied suddenly and held fixed at node 4. Damping of 10% of critical damping in each mode is used. With this excitation the solution for , the amplitude of the ith eigenmode, is
where is the frequency of vibration, is the fraction of critical damping, , t is time, and is the projection of the force onto the ith eigenmode. is given by
where is the force at degree of freedom N ( 0, 10 in this case), is the component of the ith eigenvector at degree of freedom N, and is the generalized mass for the ith mode.
Base acceleration—damped system
Next, the structure is excited by a constant acceleration of 1.0 at the fixed node (node 1), which is defined using base motion. It can be shown that the equations given above for force excitation can be used for this case when we define the force as
where is the modal participation factor (defined in Variables associated with the natural modes of a model).
Static preload—undamped system (one mode only)
The modal dynamic step is a linear perturbation procedure and will start from the undeformed configuration by default. However, it is also possible to start the analysis from a deformed configuration by using a static linear perturbation procedure to create the deformed configuration. This step is followed by a modal dynamic step that specifies that the starting position is the linear perturbation solution from the previous step (General and perturbation procedures). This solution is projected onto the eigenvalues to give the initial modal amplitude:
In general, this projection will preserve all the predeformation only if all of the modes of the system are included in the modal dynamic solution: if only a small number of the modes of the system are used in the modal dynamic analysis—as is the case in practical applications—this projection will only be approximate: that part of the predeformation that is orthogonal to the modes included in the analysis will be lost.
In this analysis an initial displacement of 1.0 is given to node 4 using a boundary condition at this node in a static linear perturbation procedure. The frequency step is then done with the restraint at node 4 removed so that this node is free to vibrate in the subsequent modal dynamic step. (It is essential that the boundary condition be removed before the eigenvalue problem is solved for the natural modes of the system. Otherwise, incorrect modes—with the boundary condition still in place—will be obtained.) Only one mode is used, so some part of the static response is lost in the projection onto this mode.
At the beginning of the modal dynamic step that carries over initial conditions, Abaqus calculates the initial values of the modal amplitude, using the equation given above, as 0.8293 for displacement normalization and 0.4779 for mass normalization. With no damping the response will, therefore, be
for displacement normalization and
for mass normalization.
![]()
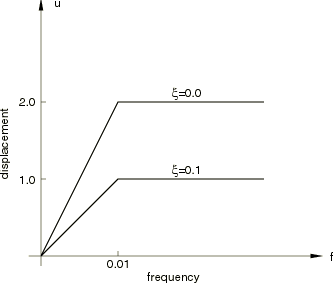
Response spectrum analysis
The displacement response spectra shown in Figure 1 are used in the next analysis. Spectra are defined in the figure for no damping and for 10% of critical damping in each mode. In this example 2% of critical damping is used so that the logarithmic interpolation gives a magnitude of 1.7411 for the maximum displacement for each mode. The analysis is done for two cases: absolute summation of the contributions from each mode and the square root of the sum of the squares (SRSS) summation. Since frequencies are well separated in this case, the use of the ten-percent summation method will give results that are identical to the SRSS method, the complete quadratic combination response will differ only by a small amount from SRSS (because of very small cross-correlation factors between the modes), and the Naval Research Laboratory summation method will calculate results that are very close to the absolute summation. For a comparison of all five summation rules, see Response spectra of a three-dimensional frame building. Absolute summation means that the peak displacement response is estimated as
where is the displacement at degree of freedom k, is the ith eigenmode in degree of freedom k, is the maximum value for the amplitude in the ith mode, and is found from the appropriate spectrum definition S given in the input. In this case S is represented by displacement spectrum , applied in the global x-direction. SRSS summation estimates the peak displacement response as
![]()
Steady-state analysis
The steady-state analysis procedure is verified by exciting the model over a range of frequencies. A load of the form
where is the forcing frequency and 5, is applied to node 4 in the x-direction.
Two kinds of damping are available for this type of analysis. One is modal damping, which defines the damping term for a mode as
where is the fraction of critical damping. The other is structural damping, for which the damping force is defined as
where and is the structural damping factor.
Abaqus provides output as the response amplitude, , and phase angle, , for the ith mode. For this example, with only the real loads applied, the exact solution—with both modal and structural damping present—is
and
where is the amplitude of the forcing function, , projected onto the ith mode.
The input file rodlindynamic_ssdynamics.inp requests a steady-state dynamic analysis for the forcing frequency range from 0.01 to 10 cycles/time. All three mode shapes are extracted with a frequency step and are used throughout the steady-state analysis, as indicated by the modal damping definition, where the damping value is defined to be 10% of critical damping in each mode.
![]()
Random response analysis
The same rod model with structural damping present is now exposed to nondeterministic loading. The case we consider is uncorrelated white noise applied to all nodes. The exact solution for the cross-spectral density matrix of the modal amplitudes (the generalized coordinates) as a function of frequency, , for continuously distributed white noise is
where
is the complex frequency response function for mode , with the generalized mass for the mode, the frequency of the mode, and the structural damping used with the mode; is the complex conjugate of ; and ) is the cross-spectral density matrix of the external loading. Abaqus assumes that the integrated projection of the cross-spectral density matrix onto the eigenmodes can be expressed as a matrix between the loaded nodal degrees of freedom projected onto the eigenmodes, so
is defined by applying nodal loads, (where N refers to a degree of freedom in the model and I refers to the load case number) and giving a matrix of scaling factors, , and corresponding frequency functions, , for each load case. Here J refers to the matrix of scaling factors by which to scale in load case I. is then defined as
In this case we need only one load case, 1, and one frequency function and associated matrix of scaling factors, 1. (See Random response to jet noise excitation for a problem in which several frequency functions and scaling factor matrices are needed to define the cross-spectral density matrix of the loading.) Since white noise is assumed to be uncorrelated, is defined as a diagonal matrix: 0 for Uncorrelated loadings are specified using a correlation definition, where is defined. We choose a unit magnitude for the scaling factors so that becomes a unit matrix. Since the diagonal terms of the cross-spectral density matrix are the power spectral density functions of the loading, the cross-spectral density matrix will be a real diagonal matrix. Therefore, imaginary frequency functions and scaling factors need not be considered here. As a result, the power spectral definition is a reference power spectral density function (rather than a general frequency function), , which is scaled by the product of load magnitudes, (and by , but is a unit matrix). We apply loads of 10 to each of nodes 2 and 3 and a load of 5 to node 4, corresponding to a unit load distributed continuously along the rod.
At a frequency of 0.1 cycles/time is, therefore,
The cross-spectral density matrices for the displacements, velocities, and accelerations of the nodes can be calculated directly from . For example, the cross-spectral density matrix of the displacements is
![]()
Results and discussion
The results of the various calculations for this example are given in tables in the text below. In all cases the Abaqus results agree with the exact solution.
Modal dynamic analysis: tip load–damped system
Results for the three generalized coordinates in this model at times of 0.1, 0.2, and 0.3 for displacement normalization are:
| Time | Mode | |||
|---|---|---|---|---|
| 0.1 | 1 | 0.149 | 2.96 | 29.2 |
| 2 | −0.146 | −2.87 | −27.0 | |
| 3 | 0.144 | 2.80 | 25.3 | |
| 0.2 | 1 | 0.589 | 5.82 | 28.0 |
| 2 | −0.560 | −5.32 | −21.8 | |
| 3 | 0.538 | 4.94 | 16.9 | |
| 0.3 | 1 | 1.31 | 8.55 | 26.5 |
| 2 | −1.19 | −7.17 | −15.0 | |
| 3 | 1.10 | 6.12 | 6.53 |
The results for mass normalization are:
| Time | Mode | |||
|---|---|---|---|---|
| 0.1 | 1 | 0.0859 | 1.71 | 16.8 |
| 2 | 0.0843 | 1.66 | 15.6 | |
| 3 | −0.0831 | −1.62 | −14.6 | |
| 0.2 | 1 | 0.340 | 3.36 | 16.2 |
| 2 | 0.323 | 3.07 | 12.6 | |
| 3 | −0.311 | −2.85 | −9.77 | |
| 0.3 | 1 | 0.756 | 4.94 | 15.3 |
| 2 | 0.687 | 4.14 | 8.65 | |
| 3 | −0.635 | −3.53 | −3.77 |
The signs of the generalized coordinates may change depending on the sign of the corresponding eigenvectors.
Physical values are obtained by summation of the modal values at each time:
where a is a physical quantity and is the value of this quantity computed for mode i.
For the stress and strain in the elements in this structure this gives the following results:
| Time | Element | Stress | Strain |
|---|---|---|---|
| 0.1 | 1 | 0.000206 | 0.000041 |
| 2 | 0.001870 | 0.000374 | |
| 3 | 0.2173 | 0.043452 | |
| 0.2 | 1 | 0.001797 | 0.000359 |
| 2 | 0.020377 | 0.004076 | |
| 3 | 0.8210 | 0.1642 | |
| 0.3 | 1 | 0.007051 | 0.001410 |
| 2 | 0.083857 | 0.016771 | |
| 3 | 1.708 | 0.3416 |
The values for nodal variables are calculated using the same summation method, so the displacements, velocities, accelerations, and reaction forces are:
| Time | Node | Displacement | Velocity | Acceleration | Reaction force |
|---|---|---|---|---|---|
| 0.1 | 1 | 0.0 | 0.0 | 0.0 | −0.000412 |
| 2 | 0.00041 | 0.0126 | 0.2632 | ||
| 3 | 0.00415 | 0.1394 | 3.363 | ||
| 4 | 0.4387 | 8.630 | 81.42 | ||
| 0.2 | 1 | 0.0 | 0.0 | 0.0 | −0.003595 |
| 2 | 0.00359 | 0.0583 | 0.6979 | ||
| 3 | 0.0444 | 0.7689 | 9.602 | ||
| 4 | 1.686 | 16.08 | 66.71 | ||
| 0.3 | 1 | 0.0 | 0.0 | 0.0 | −0.014102 |
| 2 | 0.01410 | 0.1660 | 1.547 | ||
| 3 | 0.1818 | 2.110 | 17.33 | ||
| 4 | 3.598 | 21.84 | 48.06 |
Modal dynamic analysis: tip load–undamped system
Time history response is also obtained for an undamped system. The results for the generalized coordinates for displacement normalization are:
| Time | Mode | |||
|---|---|---|---|---|
| 0.1 | 1 | 0.150 | 2.99 | 29.8 |
| 2 | −0.149 | −2.96 | −28.7 | |
| 3 | 0.148 | 2.92 | 27.5 | |
| 0.2 | 1 | 0.598 | 5.95 | 29.3 |
| 2 | −0.582 | −5.65 | −24.8 | |
| 3 | 0.567 | 5.35 | 20.5 | |
| 0.3 | 1 | 1.34 | 8.84 | 28.4 |
| 2 | −1.26 | −7.83 | −18.6 | |
| 3 | 1.19 | 6.90 | 10.0 |
The results for mass normalization are:
| Time | Mode | |||
|---|---|---|---|---|
| 0.1 | 1 | 0.0865 | 1.73 | 17.2 |
| 2 | 0.0860 | 1.71 | 16.6 | |
| 3 | −0.0854 | −1.68 | −15.9 | |
| 0.2 | 1 | 0.345 | 3.44 | 16.9 |
| 2 | 0.336 | 3.26 | 14.3 | |
| 3 | −0.327 | −3.09 | −11.8 | |
| 0.3 | 1 | 0.772 | 5.10 | 16.4 |
| 2 | 0.728 | 4.52 | 10.8 | |
| 3 | −0.686 | −3.98 | −5.80 |
Modal dynamic analysis: base acceleration–damped system
With the modal damping set to 10% of critical damping for all three modes, the responses of the three generalized coordinates to this base acceleration for displacement normalization are:
| Time | Mode | |||
|---|---|---|---|---|
| 0.1 | 1 | −0.00617 | −0.123 | −1.21 |
| 2 | −0.00162 | −0.0319 | −0.30 | |
| 3 | −0.00043 | −0.00834 | −0.0753 | |
| 0.2 | 1 | −0.02442 | −0.241 | −1.16 |
| 2 | −0.00622 | −0.05912 | −0.242 | |
| 3 | −0.00160 | −0.01469 | −0.0504 | |
| 0.3 | 1 | −0.05428 | −0.355 | −1.10 |
| 2 | −0.01322 | −0.07966 | −0.167 | |
| 3 | −0.003272 | −0.01821 | −0.01944 |
The results for mass normalization are:
| Time | Mode | |||
|---|---|---|---|---|
| 0.1 | 1 | −0.00356 | −0.0709 | −0.698 |
| 2 | 0.000936 | 0.0184 | 0.173 | |
| 3 | 0.000247 | 0.00481 | 0.0435 | |
| 0.2 | 1 | −0.0140 | −0.139 | −0.671 |
| 2 | 0.00359 | 0.0341 | 0.140 | |
| 3 | 0.000924 | 0.00848 | 0.0291 | |
| 0.3 | 1 | −0.0313 | −0.205 | −0.636 |
| 2 | 0.00763 | 0.0460 | 0.0962 | |
| 3 | 0.00189 | 0.0105 | 0.0112 |
These responses give the following results for the nodal variables. (In this table, as in the Abaqus output, the displacement, velocity, and acceleration values are normally given relative to the base motion: total displacement values are also given.)
| Time | Node | Displacement | Velocity | Acceleration | Total displacement |
|---|---|---|---|---|---|
| 0.1 | 1 | 0.0 | 0.0 | 0.0 | 0.0050000 |
| 2 | −0.00492 | −0.0974 | −0.9421 | 0.0000797 | |
| 3 | −0.00497 | −0.0991 | −0.9824 | 0.0000290 | |
| 4 | −0.00498 | −0.0993 | −0.9853 | 0.0000244 | |
| 0.2 | 1 | 0.0 | 0.0 | 0.0 | 0.0200000 |
| 2 | −0.01923 | −0.1872 | −0.8478 | 0.0007692 | |
| 3 | −0.01976 | −0.1964 | −0.9623 | 0.0002365 | |
| 4 | −0.01980 | −0.1970 | −0.9700 | 0.0001965 | |
| 0.3 | 1 | 0.0 | 0.0 | 0.0 | 0.0450000 |
| 2 | −0.04200 | −0.2661 | −0.7266 | 0.0030027 | |
| 3 | −0.04417 | −0.2914 | −0.9364 | 0.0008259 | |
| 4 | −0.04433 | −0.2932 | −0.9536 | 0.0006692 |
Modal dynamic analysis: static preload–undamped system (one mode only)
The results for the modal amplitude for displacement normalization are:
| Time | |
|---|---|
| 0.06 | 0.828 |
| 1.43 | 0.0004 |
| 2.86 | −0.829 |
| 5.32 | 0.750 |
| 5.72 | 0.829 |
The results for mass normalization are:
| Time | |
|---|---|
| 0.06 | 0.478 |
| 1.43 | 0.0003 |
| 2.86 | −0.479 |
| 5.32 | 0.433 |
| 5.72 | 0.479 |
Response spectrum analysis
The response spectrum analysis gives the following results for the nodal displacements:
| Node | Displacement | Displacement |
|---|---|---|
| (abs. summation) | (SSRS) | |
| 1 | 0.0 | 0.0 |
| 2 | 1.741 | 1.231 |
| 3 | 2.010 | 1.881 |
| 4 | 2.902 | 2.248 |
Steady-state analysis
The results for the amplitude and phase angle of the generalized displacements (the modal amplitudes, ) for displacement normalization are shown in the table below:
| Forcing | Mode | Amplitude, | Phase, |
|---|---|---|---|
| frequency | |||
| 0.01 | 1 | 12.48 | −0.66 |
| 2 | 1.667 | 179.8 | |
| 3 | 0.8934 | −0.1757 | |
| 0.175 | 1 | 62.2 | −90.0 |
| 2 | 1.918 | 175.2 | |
| 3 | 0.9607 | −3.304 | |
| 0.477 | 1 | 1.918 | −175.2 |
| 2 | 8.333 | 90.0 | |
| 3 | 1.835 | −17.51 |
The results for mass normalization are shown in the table below:
| Forcing | Mode | Amplitude, | Phase, |
|---|---|---|---|
| frequency | |||
| 0.01 | 1 | 7.705 | −0.66 |
| 2 | 0.9627 | 179.8 | |
| 3 | 0.5158 | −0.1757 | |
| 0.175 | 1 | 35.91 | −90.0 |
| 2 | 1.107 | 175.2 | |
| 3 | 0.5546 | −3.304 | |
| 0.477 | 1 | 1.107 | −175.2 |
| 2 | 4.811 | 90.0 | |
| 3 | 1.060 | −17.51 |
Stress and strain amplitudes for element 1 and the amplitude of the reaction force at node 1 are:
| Forcing | Stress | Strain | Reaction force, |
|---|---|---|---|
| frequency | node 1 | ||
| 0.01 | 2.51 | 0.5019 | 5.019 |
| 0.175 | 15.50 | 3.10 | 31.00 |
| 0.477 | 3.988 | 0.7977 | 7.977 |
Output of the phase angle can be requested for any variable. For example, the stress in element 1 at a forcing frequency of 0.477 cycles/time has an amplitude of 3.988 and a phase angle of 90.58° with respect to the forcing function.
A third step is included in which the steady-state solution is calculated with 10% structural damping. At low frequencies ( 0.01) the results for this step do not differ very much from the results using modal damping, but significant differences appear at forcing frequencies in the range of the eigenfrequencies of the structure.
Random response analysis
Abaqus provides the diagonal terms of the cross-spectral density matrix; i.e., the power spectral densities. The power spectral densities of displacement, velocity, and acceleration at 0.1 cycles/time are:
| Node | Displacement | Velocity | Acceleration |
|---|---|---|---|
| 2 | 469.1 | 185.2 | 73.12 |
| 3 | 1311. | 517.6 | 204.3 |
| 4 | 1628. | 642.7 | 253.7 |
Root mean square values are calculated as the square roots of the variances, which are the integrals of the power spectral densities up to the frequency of interest. The root mean square values of the nodal variables at 1 Hz are:
| Node | RMS value | RMS value | RMS value |
|---|---|---|---|
| of displacement | of velocity | of acceleration | |
| 2 | 81.51 | 134.0 | 353.7 |
| 3 | 129.3 | 158.0 | 334.2 |
| 4 | 152.9 | 207.4 | 485.6 |
The power spectral densities and the RMS values of stress and strain throughout the model are likewise calculated from and the modal vectors of the stress and strain.
![]()
Input files
- rodlindynamic_modal_subeigen.inp
MODAL DYNAMIC analysis with a damping value of 0.1 and the structure excited by a point load applied at node 4.
- rodlindynamic_respspec_subeigen.inp
RESPONSE SPECTRUM analysis.
- rodlindynamic_ssdyn_subeigen.inp
STEADY STATE DYNAMICS analysis with modal and structural damping for the given range of forcing frequencies.
- rodlindynamic_random_subeigen.inp
RANDOM RESPONSE analysis with structural damping.
- rodlindynamic_correlationdata.inp
Contains the correlation definition for use inrodlindynamic_random.inp.
- rodlindynamic_composite.inp
MODAL DYNAMIC analysis with composite modal damping.
- rodlindynamic_modal_nodamp.inp
MODAL DYNAMIC analysis with damping set to 0.
- rodlindynamic_modal_base.inp
MODAL DYNAMIC analysis with BASE MOTION.
- rodlindynamic_modal_preload.inp
MODAL DYNAMIC analysis in which the excitation is caused by a static preloading of the structure, with the load removed suddenly to cause the dynamic event.
- rodlindynamic_modal_base2.inp
MODAL DYNAMIC analysis with BASE MOTION using the secondary base motion and composite modal damping.
- rodlindynamic_modal.inp
Same as rodlindynamic_modal_subeigen.inp, except that it uses the Lanczos solver and the eigenvectors are normalized with respect to the generalized mass.
- rodlindynamic_respspect.inp
Same as rodlindynamic_respspec_subeigen.inp, except that it uses the Lanczos solver and the eigenvectors are normalized with respect to the generalized mass.
- rodlindynamic_ssdyn_massnorm.inp
Same as rodlindynamic_ssdyn_subeigen.inp, except that the eigenvectors are normalized with respect to the generalized mass. The subspace iteration solver is used.
- rodlindynamic_random_massnorm.inp
Same as rodlindynamic_random_subeigen.inp, except that the eigenvectors are normalized with respect to the generalized mass. The subspace iteration solver is used.
- rodlindynamic_ssdynamics.inp
Same as rodlindynamic_ssdyn_subeigen.inp, except that the Lanczos solver is used. The eigenvectors are normalized with respect to the maximum displacement.
- rodlindynamic_random.inp
Same as rodlindynamic_random_subeigen.inp, except that the Lanczos solver is used. The eigenvectors are normalized with respect to the maximum displacement.
![]()
Figures