About Typical Optimization Tasks for Modal Analysis

Often the design target is to increase the first eigenfrequencies in an eigenfrequency spectrum. It is important to consider more than the first natural eigenfrequency when increasing the natural frequencies using optimization. Otherwise, the first and secondary mode might switch during the optimization as shown in the figure below.

Optimizing all the lowest eigenfrequencies using the Kreisselmaier-Steinhauser formulation is demonstrated in figure (b) and the single lowest eigenfrequency using mode tracking is shown in figure (a):

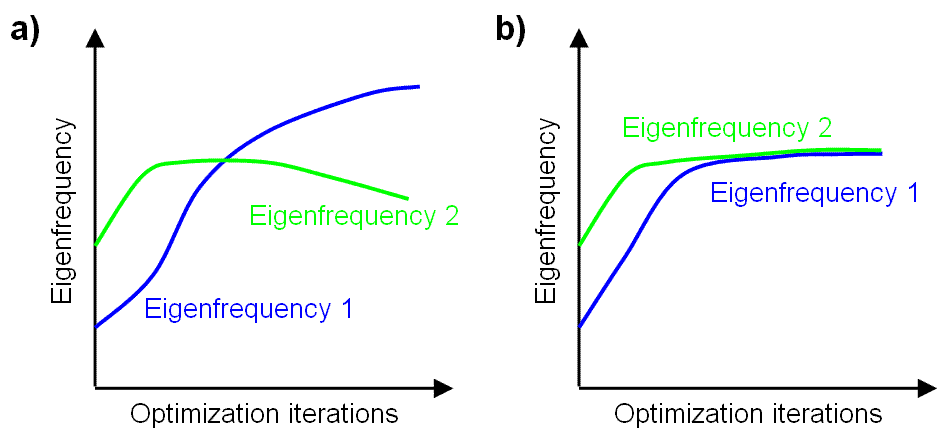For some optimization problems it can be desirable that a sudden eigenfrequency is increased whereas the other eigenfrequencies are allowed to decrease (see figure (a)).

• Maximizing the First Eigenfrequencies describes how several lowest eigenfrequencies are increased (see figure (b)).
• Maximizing the Eigenfrequency of a Certain Eigenmode addresses how a specific eigenfrequency in an eigenfrequency spectrum is optimized using mode tracking (see figure (a)).
• Maximizing the Band Gap describes how a band gap in the eigenfrequency spectrum can be designed. A band gap in the eigenfrequency spectrum contains no eigenfrequencies.
• Constraining an Eigenfrequencyshows how an eigenfrequency can be applied in a constraint, e.g. when maximizing the stiffness under the condition that the first eigenfrequency is above 100 Hz or when minimizing the mass under the condition that the eigenfrequencies are below or above certain specified values.