Models for metals subjected to cyclic loading | ||||||
|
| |||||
ProductsAbaqus/StandardAbaqus/Explicit
The kinematic hardening models in Abaqus are intended to simulate the behavior of metals that are subjected to cyclic loading. These models are typically applied to studies of low-cycle fatigue and ratchetting. The basic concept of these models is that the yield surface shifts in stress space so that straining in one direction reduces the yield stress in the opposite direction, thus simulating the Bauschinger effect and anisotropy induced by work hardening.
Three kinematic hardening models are available in Abaqus. The simplest model provides linear kinematic hardening and is, thus, mainly used for low-cycle fatigue evaluations. This model yields physically reasonable results if the uniaxial behavior is linearized in the plastic range (a constant work-hardening slope). This is usually best accomplished by guessing the strain levels that will be attained in the problem and linearizing the actual material behavior accordingly. It is important to recognize this restriction on the theory's ability to provide reasonable results and to provide material data accordingly. This model is available with the Mises or Hill yield surface.
The combined isotropic/kinematic hardening model is an extension of the linear model. It provides a more accurate approximation to the stress-strain relation than the linear model. It also models other phenomena—such as ratchetting, relaxation of the mean stress, and cyclic hardening—that are typical of materials subjected to cyclic loading. In addition, it is possible to superpose several kinematic hardening models, which in general will produce more accurate results when the range of changes in strain is significant and will allow more accurate modeling of the ratchetting effect. This model is available only with the Mises yield surface.
The multilinear kinematic model, available only in Abaqus/Standard, combines several piecewise linear hardening curves to predict the complex behavior of materials. This model is very easy to calibrate and is defined by giving the value of the uniaxial yield stress as a function of uniaxial plastic strain, temperature, or field variables. It can be used to model the Bauschinger effect but cannot predict ratchetting.
This section first describes those aspects of the formulation that are common to these models; the specific formulation of each model is presented subsequently.
Strain rate decomposition
The total strain rate is written in terms of the elastic and plastic strain rates as
![]()
Elastic behavior
The elastic behavior can be modeled only as linear elastic
where represents the fourth-order elasticity tensor and and are the second-order stress and strain tensors, respectively.
![]()
Plastic behavior
The models are pressure-independent plasticity models. For both the linear kinematic hardening model and the combined isotropic/kinematic hardening model, the yield surface is defined by the function
where is the equivalent Mises stress or Hill's potential with respect to the backstress or “kinematic shift” and is the size of the yield surface. For example, the equivalent Mises stress is defined as
where is the deviatoric part of the backstress and is the deviatoric stress tensor. Both of these models assume associated plastic flow:
where represents the rate of plastic flow and is the equivalent plastic strain rate,
In the multilinear kinematic hardening model, the response is assumed to be a weighted sum of various elastic-perfectly plastic elements. Each of these elements, also referred to as subvolumes, use the Mises yield surface with different yield strength. The flow rule for the multilinear kinematic hardening model is as follows:
where is the total number of subvolumes, , , and are the weights, Mises yield surface, equivalent plastic strain rate, and the stress of the kth subvolume, respectively. Every subvolume follows an associated flow rule.
![]()
Linear kinematic hardening model
This model is the simplest of all the kinematic hardening models available in Abaqus. The size of the yield surface, , can be a function of temperature only for this model. The evolution of is defined by Ziegler's hardening rule, generalized to the nonisothermal case as
where is the hardening parameter ( is the work-hardening slope of the isothermal uniaxial stress-strain response, , taken at different temperatures) and is the rate of change of C with respect to time. This form of evolution law for defines the rate of due to plastic straining to be in the direction of the current radius vector from the center of the yield surface, , and the rate due to temperature changes to be toward the origin of stress space. The inclusion of the term in the evolution of ensures that the material response is temperature history independent and, consequently, can be characterized with isothermal data. Rice (1975) writes this concept quite generally as
The particular identification of and in Equation 6 above is assumed, so the material behavior is defined by the isothermal, uniaxial work hardening data, only.
![]()
Nonlinear isotropic/kinematic hardening model
This model is based on the work of Lemaitre and Chaboche (1990). The size of the yield surface, , is defined as a function of equivalent plastic strain, ; temperature, ; and field variables, . This dependency can be provided directly, can be coded in user subroutine UHARD, or can be modeled with a simple exponential law for materials that either cyclically harden or soften as
where is the yield surface size at zero plastic strain, and and are additional material parameters that must be calibrated from cyclic test data.
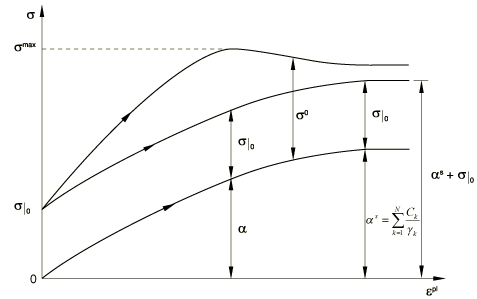
The overall backstress is composed of multiple backstress components, where the evolution of the backstress components of the model is defined as
and the overall backstress is computed from the relation
where N is the number of backstresses, and are material parameters, and is the rate of change of with respect to temperature and field variables. This equation is the basic Ziegler law, generalized to account for temperature and field-variable dependency of and to which a “recall” term, , has been added. The recall term introduces nonlinearity in the evolution law. The rate of change of with respect to temperature and field variables is not accounted for in the evolution law for . Consequently, if vary with temperature, the material response predicted by the model will be temperature history dependent. However, it can be shown that this dependency on temperature history is small and fades away with increasing plastic deformation. The condition for complete temperature history independent behavior is to use constant values for .
The evolution of the backstress and the isotropic hardening are illustrated in Figure 1 for unidirectional loading and in Figure 2 for multiaxial loading.
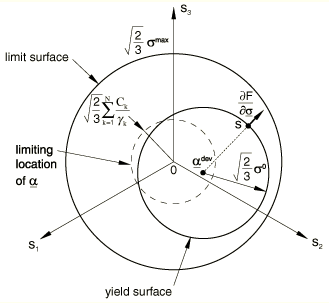
The center of the yield surface is contained within a cylinder of radius , which follows directly from Equation 10. Therefore, the yield surface is contained within the limiting surface of radius , as shown in the figures. This model can be degenerated into the linear kinematic model described above by setting and , for .
The physical behavior that can be captured by this model, as well as its limitations, is described in detail in Models for metals subjected to cyclic loading.
![]()
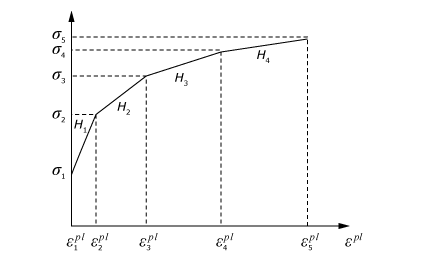
Multilinear kinematic hardening model
The multilinear kinematic hardening model is defined by giving the value of uniaxial yield stress as a function of uniaxial plastic strain (Figure 3). The number of stress-plastic strain pairs given on the input curve determines the number of subvolumes, , in the model. The yield strength of the kth subvolume () is calculated as
where () is the stress-plastic strain data provided by the user and is the shear modulus of the material. All the subvolumes are subjected to the same total strain, and the total stress is calculated as a weighted sum of stresses in the different subvolumes:
The weight of the kth subvolume is
where is the hardening modulus between the kth data point and the th data point on the stress versus plastic strain curve, defined by
The sum of weights over all subvolumes is one. It is assumed that the hardening modulus beyond the last data point is zero.