Models for metals subjected to cyclic loading

Yield surfaces

The kinematic hardening models used to model the behavior of metals subjected to cyclic loading are pressure-independent plasticity models; in other words, yielding of the metals is independent of the equivalent pressure stress. These models are suited for most metals subjected to cyclic loading conditions, except voided metals.

The linear kinematic hardening model can be used with the Mises or Hill yield surface. The nonlinear isotropic/kinematic model can be used only with the Mises yield surface in Abaqus/Standard and with the Mises or Hill yield surface in Abaqus/Explicit. The pressure-independent yield surface used in the linear kinematic hardening model and the nonlinear isotropic/kinematic hardening model is defined by the function

F = f (σ - α) - σ^{0} = 0,

where $σ^{0}$ is the yield stress and $f (σ - α)$ is the equivalent Mises stress or Hill's potential with respect to the backstress $α$ . For example, the equivalent Mises stress is defined as

f (σ - α) = \sqrt{\frac{3}{2} (S - α^{d e v}) : (S - α^{d e v})},

where $S$ is the deviatoric stress tensor (defined as $S = σ + p I$ , where $σ$ is the stress tensor, p is the equivalent pressure stress, and $I$ is the identity tensor) and $α^{d e v}$ is the deviatoric part of the backstress tensor.

The response in the multilinear kinematic hardening model is assumed to be a weighted sum of various elastic-perfectly plastic elements. Each of these elements, also referred to as subvolumes, uses the Mises yield surface with a different yield strength.

Flow rule

The kinematic hardening models assume associated plastic flow. The assumption of associated plastic flow is acceptable for metals subjected to cyclic loading as long as microscopic details, such as localization of plastic flow occurring as a metal component ruptures due to cyclic fatigue loads, are not of interest.

Linear kinematic hardening model and nonlinear isotropic/kinematic hardening model

In the case of the linear kinematic hardening model and the nonlinear isotropic/kinematic hardening model:

{\dot{ε}}^{p l} = {\dot{\bar{ε}}}^{p l} \frac{\partial F}{\partial σ},

where ${\dot{ε}}^{p l}$ is the rate of plastic flow and ${\dot{\bar{ε}}}^{p l}$ is the equivalent plastic strain rate.

The evolution of the equivalent plastic strain is obtained from the following equivalent plastic work expression:

σ^{0} {\dot{\bar{ε}}}^{p l} = σ : {\dot{ε}}^{p l},

which yields ${\dot{\bar{ε}}}^{p l} = \sqrt{\frac{2}{3} {\dot{ε}}^{p l} : {\dot{ε}}^{p l}}$ for isotropic Mises plasticity.

Multilinear kinematic hardening model

The flow rule for the multilinear kinematic hardening model is as follows:

{\dot{ε}}^{p l} = \sum_{k = 1}^{N} w_{k} {\dot{\bar{ε}}}_{k}^{p l} \frac{\partial F_{k}}{\partial σ_{k}},

where $N$ is the total number of subvolumes and $w_{k},$ $F_{k},$ ${\dot{\bar{ε}}}_{k}^{p l},$ and $σ_{k}$ are the weights, Mises yield surface, equivalent plastic strain rate, and the stress of the kth subvolume, respectively. Every subvolume follows an associated flow rule.

Hardening

The linear kinematic hardening model has a constant hardening modulus, and the nonlinear isotropic/kinematic hardening model has both nonlinear kinematic and nonlinear isotropic hardening components. The multilinear kinematic hardening model has a piecewise constant hardening modulus.

Linear kinematic hardening model

The evolution law of this model consists of a linear kinematic hardening component that describes the translation of the yield surface in stress space through the backstress, $α$ . When temperature dependence is omitted, this evolution law is the linear Ziegler hardening law

\dot{α} = C \frac{1}{σ^{0}} (σ - α) {\dot{\bar{ε}}}^{p l},

where ${\dot{\bar{ε}}}^{p l}$ is the equivalent plastic strain rate and C is the kinematic hardening modulus. In this model the equivalent stress defining the size of the yield surface, $σ^{0}$ , remains constant, $σ^{0} = {σ |}_{0}$ , where ${σ |}_{0}$ is the equivalent stress defining the size of the yield surface at zero plastic strain.

Nonlinear isotropic/kinematic hardening model

The evolution law of this model consists of two components: a nonlinear kinematic hardening component, which describes the translation of the yield surface in stress space through the backstress, $α$ ; and an isotropic hardening component, which describes the change of the equivalent stress defining the size of the yield surface, $σ^{0}$ , as a function of plastic deformation.

The kinematic hardening component is defined to be an additive combination of a purely kinematic term (linear Ziegler hardening law) and a relaxation term (the recall term), which introduces the nonlinearity. In addition, several kinematic hardening components (backstresses) can be superposed, which may considerably improve results in some cases. When temperature and field variable dependencies are omitted, the hardening laws for each backstress are

\dot{α_{k}} = C_{k} \frac{1}{σ^{0}} (σ - α) {\dot{\bar{ε}}}^{p l} - γ_{k} α_{k} {\dot{\bar{ε}}}^{p l},

and the overall backstress is computed from the relation

α = \overset{N}{\sum_{k = 1}} α_{k},

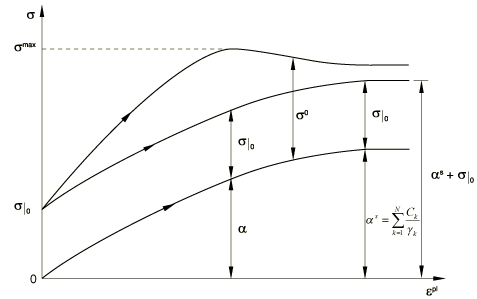
where $N$ is the number of backstresses, and $C_{k}$ and $γ_{k}$ are material parameters that must be calibrated from cyclic test data. $C_{k}$ are the initial kinematic hardening moduli, and $γ_{k}$ determine the rate at which the kinematic hardening moduli decrease with increasing plastic deformation. The kinematic hardening law can be separated into a deviatoric part and a hydrostatic part; only the deviatoric part has an effect on the material behavior. When $C_{k}$ and $γ_{k}$ are zero, the model reduces to an isotropic hardening model. When all $γ_{k}$ equal zero, the linear Ziegler hardening law is recovered. Calibration of the material parameters is discussed in Usage and calibration of the kinematic hardening models below. Figure 1 shows an example of nonlinear kinematic hardening with three backstresses.

Figure 1. Kinematic hardening model with three backstresses.

Each of the backstresses covers a different range of strains, and the linear hardening law is retained for large strains.

The isotropic hardening behavior of the model defines the evolution of the yield surface size, $σ^{0}$ , as a function of the equivalent plastic strain, ${\bar{ε}}^{p l}$ . This evolution can be introduced by specifying $σ^{0}$ directly as a function of ${\bar{ε}}^{p l}$ in tabular form, by specifying $σ^{0}$ in user subroutine UHARD (in Abaqus/Standard only), or by using the simple exponential law

σ^{0} = {σ |}_{0} + Q_{\infty} (1 - e^{- b {\bar{ε}}^{p l}}),

where ${σ |}_{0}$ is the yield stress at zero plastic strain and $Q_{\infty}$ and b are material parameters. $Q_{\infty}$ is the maximum change in the size of the yield surface, and b defines the rate at which the size of the yield surface changes as plastic straining develops. When the equivalent stress defining the size of the yield surface remains constant ( $σ^{0} = {σ |}_{0}$ ), the model reduces to a nonlinear kinematic hardening model.

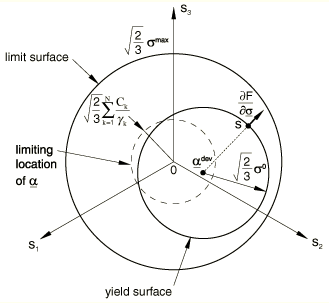
The evolution of the kinematic and the isotropic hardening components is illustrated in Figure 2 for unidirectional loading and in Figure 3 for multiaxial loading. The evolution law for the kinematic hardening component implies that the backstress is contained within a cylinder of radius $\sqrt{2 / 3} α^{s} = \sqrt{2 / 3} \sum_{k}^{N} C_{k} / γ_{k}$ , where $α^{s}$ is the magnitude of $α$ at saturation (large plastic strains). It also implies that any stress point must lie within a cylinder of radius $\sqrt{2 / 3} σ_{m a x}$ (using the notation of Figure 2) since the yield surface remains bounded. At large plastic strain any stress point is contained within a cylinder of radius $\sqrt{2 / 3} (α^{s} + σ^{s})$ , where $σ^{s}$ is the equivalent stress defining the size of the yield surface at large plastic strain. If tabular data are provided for the isotropic component, $σ^{s}$ is the last value given to define the size of the yield surface. If user subroutine UHARD is used, this value will depend on your implementation; otherwise, $σ^{s} = {σ |}_{0} + Q_{\infty}$ .

Figure 2. One-dimensional representation of the hardening in the nonlinear isotropic/kinematic model.

Figure 3. Three-dimensional representation of the hardening in the nonlinear isotropic/kinematic model.

Multilinear kinematic hardening model

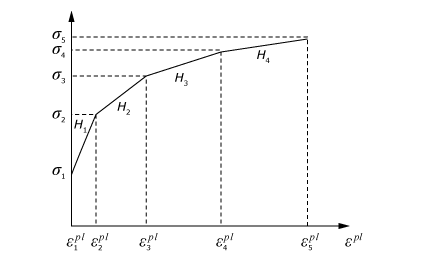
The multilinear kinematic hardening model is defined by giving the value of uniaxial yield stress as a function of uniaxial plastic strain (Figure 4). The number of stress-plastic strain pairs given on the input curve determines the number of subvolumes, $N$ , in the model. The yield strength of the kth subvolume ( $σ_{y, k}$ ) is calculated as

σ_{y, k} = σ_{k} + 3 μ ϵ_{k}^{p l},

where ( $σ_{k}, ϵ_{k}^{p l}$ ) is the user-specified stress-plastic strain data and $μ$ is the shear modulus of the material. All the subvolumes are subjected to the same total strain, and the total stress is calculated as a weighted sum of stresses in the different subvolumes:

σ = \sum_{k = 1}^{N} w_{k} σ_{k} .

The weight of the kth subvolume is

w_{k} = \frac{3 μ}{3 μ + H_{k}} - \sum_{i = 1}^{k - 1} w_{i},

where $H_{k}$ is the hardening modulus between the kth data point and the (k +1)th data point on the stress versus plastic strain curve. The sum of the weights over all the subvolumes is one. It is assumed that the hardening modulus beyond the last data point is zero.

Figure 4. Uniaxial stress versus plastic strain curve in the case of the multilinear kinematic hardening model.

Predicted material behavior

In the kinematic hardening models the center of the yield surface moves in stress space due to the kinematic hardening component. In addition, when the nonlinear isotropic/kinematic hardening model is used, the yield surface range may expand or contract due to the isotropic component. These features allow modeling of inelastic deformation in metals that are subjected to cycles of load or temperature, resulting in significant inelastic deformation and, possibly, low-cycle fatigue failure. These models account for the following phenomena:

Bauschinger effect

This effect is characterized by a reduced yield stress upon load reversal after plastic deformation has occurred during the initial loading. This phenomenon decreases with continued cycling. The linear kinematic hardening component takes this effect into consideration, but a nonlinear component improves the shape of the cycles. Further improvement of the shape of the cycle can be obtained by using a nonlinear model with multiple backstresses. The multilinear kinematic hardening model can also be used to model this effect.

Cyclic hardening with plastic shakedown

This phenomenon is characteristic of symmetric stress- or strain-controlled experiments. Soft or annealed metals tend to harden toward a stable limit, and initially hardened metals tend to soften. Figure 5 illustrates the behavior of a metal that hardens under prescribed symmetric strain cycles.

Figure 5. Plastic shakedown.

The kinematic hardening component of the models used alone predicts plastic shakedown after one stress cycle. The combination of the isotropic component together with the nonlinear kinematic component predicts shakedown after several cycles.

Ratchetting

Unsymmetric cycles of stress between prescribed limits will cause progressive “creep” or “ratchetting” in the direction of the mean stress (Figure 6).

Figure 6. Ratchetting.

Typically, transient ratchetting is followed by stabilization (zero ratchet strain) for low mean stresses, while a constant increase in the accumulated ratchet strain is observed at high mean stresses. The nonlinear kinematic hardening component, used without the isotropic hardening component, predicts constant ratchet strain. The prediction of ratchetting is improved by adding isotropic hardening, in which case the ratchet strain may decrease until it becomes constant. However, in general the nonlinear hardening model with a single backstress predicts a too significant ratchetting effect. A considerable improvement in modeling ratchetting can be achieved by superposing several kinematic hardening models (backstresses) and choosing one of the models to be linear or nearly linear ( $γ_{k} ≪ C_{k}$ ), which results in a less pronounced ratchetting effect. The multilinear kinematic hardening model cannot predict this effect.

Relaxation of the mean stress

This phenomenon is characteristic of an unsymmetric strain experiment, as shown in Figure 7.

Figure 7. Relaxation of the mean stress.

As the number of cycles increases, the mean stress tends to zero. The nonlinear kinematic hardening component of the nonlinear isotropic/kinematic hardening model accounts for this behavior.

Limitations

The linear kinematic model is a simple model that gives only a first approximation of the behavior of metals subjected to cyclic loading, as explained above. The nonlinear isotropic/kinematic hardening model can provide more accurate results in many cases involving cyclic loading, but it still has the following limitations:

The isotropic hardening is the same at all strain ranges. Physical observations, however, indicate that the amount of isotropic hardening depends on the magnitude of the strain range. Furthermore, if the specimen is cycled at two different strain ranges, one followed by the other, the deformation in the first cycle affects the isotropic hardening in the second cycle. Thus, the model is only a coarse approximation of actual cyclic behavior. It should be calibrated to the expected size of the strain cycles of importance in the application.
The same cyclic hardening behavior is predicted for proportional and nonproportional load cycles. Physical observations indicate that the cyclic hardening behavior of materials subjected to nonproportional loading may be very different from uniaxial behavior at a similar strain amplitude.

The example problems Simple proportional and nonproportional cyclic tests, Notched beam under cyclic loading, and Uniaxial ratchetting under tension and compression illustrate the phenomena of cyclic hardening with plastic shakedown, ratchetting, and relaxation of the mean stress for the nonlinear isotropic/kinematic hardening model, as well as its limitations.

Usage and calibration of the kinematic hardening models

The linear kinematic model approximates the hardening behavior with a constant rate of hardening. This hardening rate should be matched to the average hardening rate measured in stabilized cycles over a strain range corresponding to that expected in the application. A stabilized cycle is obtained by cycling over a fixed strain range until a steady-state condition is reached; that is, until the stress-strain curve no longer changes shape from one cycle to the next. The multilinear kinematic hardening model does not have the restriction of a constant hardening rate. The more general nonlinear model will give better predictions but requires more detailed calibration.

Linear kinematic hardening model

The test data obtained from a half cycle of a unidirectional tension or compression experiment must be linearized, since this simple model can predict only linear hardening. The data are usually based on measurements of the stabilized behavior in strain cycles covering a strain range corresponding to the strain range that is anticipated to occur in the application. Abaqus expects you to provide only two data pairs to define this linear behavior: the yield stress, ${σ |}_{0}$ , at zero plastic strain and a yield stress, $σ$ , at a finite plastic strain value, $ε^{p l}$ . The linear kinematic hardening modulus, C, is determined from the relation

C = \frac{σ - {σ |}_{0}}{ε^{p l}} .

You can provide several sets of two data pairs as a function of temperature to define the variation of the linear kinematic hardening modulus with respect to temperature. If the Hill yield surface is desired for this model, you must specify a set of yield ratios, $R_{i j}$ , independently (see Anisotropic yield/creep for information on how to specify the yield ratios).

This model gives physically reasonable results for only relatively small strains (less than 5%).

Input File Usage

PLASTIC, HARDENING=KINEMATIC

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: Hardening: Kinematic

Nonlinear isotropic/kinematic hardening model

The evolution of the equivalent stress defining the size of the yield surface, $σ^{0}$ , as a function of the equivalent plastic strain, ${\bar{ε}}^{p l}$ , defines the isotropic hardening component of the model. You can define this isotropic hardening component through an exponential law or directly in tabular form. It need not be defined if the yield surface remains fixed throughout the loading. In Abaqus/Explicit if the Hill yield surface is desired for this model, you must specify a set of yield ratios, $R_{i j}$ , independently (see Anisotropic yield/creep for information on how to specify the yield ratios). The Hill yield surface cannot be used with this model in Abaqus/Standard.

The material parameters $C_{k}$ and $γ_{k}$ determine the kinematic hardening component of the model. Abaqus offers three different ways of providing data for the kinematic hardening component of the model: the parameters $C_{k}$ and $γ_{k}$ can be specified directly, half-cycle test data can be given, or test data obtained from a stabilized cycle can be given. The experiments required to calibrate the model are described below.

Defining the isotropic hardening component by the exponential law

Specify the material parameters of the exponential law ${σ |}_{0}$ , $Q_{\infty}$ , and b directly if they are already calibrated from test data. These parameters can be specified as functions of temperature and/or field variables.

Input File Usage

CYCLIC HARDENING, PARAMETERS

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: SuboptionsCyclic Hardening: toggle on Use parameters.

Defining the isotropic hardening component by tabular data

Isotropic hardening can be introduced by specifying the equivalent stress defining the size of the yield surface, $σ^{0}$ , as a tabular function of the equivalent plastic strain, ${\bar{ε}}^{p l}$ . The simplest way to obtain these data is to conduct a symmetric strain-controlled cyclic experiment with strain range $Δ ε$ . Since the material's elastic modulus is large compared to its hardening modulus, this experiment can be interpreted approximately as repeated cycles over the same plastic strain range $Δ ε^{p l} \approx Δ ε - 2 σ_{1}^{t} / E$ (using the notation of Figure 8, where E is the Young's modulus of the material).

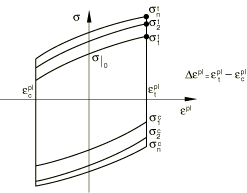
Figure 8. Symmetric strain cycle experiment.

The equivalent stress defining the size of the yield surface is ${σ |}_{0}$ at zero equivalent plastic strain; for the peak tensile stress points it is obtained by isolating the kinematic component from the yield stress (see Figure 2) as

σ_{i}^{0} = σ_{i}^{t} - α_{i}

for each cycle i, where $α_{i} = (σ_{i}^{t} + σ_{i}^{c}) / 2$ . Since the model predicts approximately the same backstress value in each cycle at a particular strain level, $α_{i} \approx (σ_{1}^{t} + σ_{1}^{c}) / 2$ . The equivalent plastic strain corresponding to $σ_{i}^{0}$ is

{\bar{ε}}_{i}^{p l} = \frac{1}{2} (4 i - 3) Δ ε^{p l} .

Data pairs ( $σ_{i}^{0}$ , ${\bar{ε}}_{i}^{p l}$ ), including the value ${σ |}_{0}$ at zero equivalent plastic strain, are specified in tabulated form. The tabulated values defining the size of the yield surface should be provided for the entire equivalent plastic strain range to which the material may be subjected. The data can be provided as functions of temperature and/or field variables.

To obtain accurate cyclic hardening data, such as would be needed for low-cycle fatigue calculations, the calibration experiment should be performed at a strain range, $Δ ε$ , that corresponds to the strain range anticipated in the analysis because the material model does not predict different isotropic hardening behavior at different strain ranges. This limitation also implies that, even though a component is made from the same material, it may have to be divided into several regions with different hardening properties corresponding to different anticipated strain ranges. Field variables and field variable dependence of these properties can also be used for this purpose.

Abaqus allows the specification of strain rate effects in the isotropic component of the nonlinear isotropic/kinematic hardening model. The rate-dependent isotropic hardening data can be defined by specifying the equivalent stress defining the size of the yield surface, $σ^{0}$ , as a tabular function of the equivalent plastic strain, ${\bar{ε}}^{p l}$ , at different values of the equivalent plastic strain rate, ${\dot{\bar{ε}}}^{p l}$ .

Input File Usage

Use the following option to define isotropic hardening with tabular data:

CYCLIC HARDENING

Use the following option to define rate-dependent isotropic hardening with tabular data:

CYCLIC HARDENING, RATE= ${\dot{\bar{ε}}}^{p l}$

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: Hardening: Combined: SuboptionsCyclic Hardening

Defining the isotropic hardening component in a user subroutine in Abaqus/Standard

Specify $σ^{0}$ directly in user subroutine UHARD. $σ^{0}$ may be dependent on equivalent plastic strain and temperature. This method cannot be used if the kinematic hardening component is specified by using half-cycle test data.

Input File Usage

CYCLIC HARDENING, USER

Abaqus/CAE Usage

You cannot define the isotropic hardening component in user subroutine UHARD in Abaqus/CAE.

Defining the kinematic hardening component by specifying the material parameters directly

The parameters $C_{k}$ and $γ_{k}$ can be specified directly as a function of temperature and/or field variables if they are already calibrated from test data. When $γ_{k}$ depend on temperature and/or field variables, the response of the model under thermomechanical loading will generally depend on the history of temperature and/or field variables experienced at a material point. This dependency on temperature-history is small and fades away with increasing plastic deformation. However, if this effect is not desired, constant values for $γ_{k}$ should be specified to make the material response completely independent of the history of temperature and field variables. The algorithm currently used to integrate the nonlinear isotropic/kinematic hardening model provides accurate solutions if the values of $γ_{k}$ change moderately in an increment due to temperature and/or field variable dependence; however, this algorithm may not yield a solution with sufficient accuracy if the values of $γ_{k}$ change abruptly in an increment.

Input File Usage

PLASTIC, HARDENING=COMBINED, DATA TYPE=PARAMETERS, NUMBER BACKSTRESSES=n

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: Hardening: Combined, Data type: Parameters, Number of backstresses: n

Defining the kinematic hardening component by specifying half-cycle test data

If limited test data are available, $C_{k}$ and $γ_{k}$ can be based on the stress-strain data obtained from the first half cycle of a unidirectional tension or compression experiment. An example of such test data is shown in Figure 9. This approach is usually adequate when the simulation will involve only a few cycles of loading.

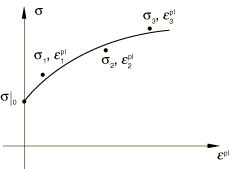
Figure 9. Half cycle of stress-strain data.

For each data point ( $σ_{i}, ε_{i}^{p l}$ ) a value of $α_{i}$ ( $α_{i}$ is the overall backstress obtained by summing all the backstresses at this data point) is obtained from the test data as

α_{i} = σ_{i} - σ_{i}^{0},

where $σ_{i}^{0}$ is the user-defined size of the yield surface at the corresponding plastic strain for the isotropic hardening component or the initial yield stress if the isotropic hardening component is not defined.

Integration of the backstress evolution laws over a half cycle yields the expressions

α_{k} = \frac{C_{k}}{γ_{k}} (1 - e^{- γ_{k} ε^{p l}}),

which are used for calibrating $C_{k}$ and $γ_{k}$ .

When test data are given as functions of temperature and/or field variables, Abaqus determines several sets of material parameters ( $C_{1}$ , $γ_{1}$ ,..., $C_{N}$ , $γ_{N}$ ), each corresponding to a given combination of temperature and/or field variables. Generally, this results in temperature-history (and/or field variable-history) dependent material behavior because the values of $γ_{k}$ vary with changes in temperature and/or field variables. This dependency on temperature-history is small and fades away with increasing plastic deformation. However, you can make the response of the material completely independent of the history of temperature and field variables by using constant values for the parameters $γ_{k}$ . This can be achieved by running a data check analysis first; an appropriate constant values of $γ_{k}$ can be determined from the information provided in the data file during the data check. The values for the parameters $C_{k}$ and the constant parameters $γ_{k}$ can then be entered directly as described above.

If the model with multiple backstresses is used, Abaqus obtains hardening parameters for different values of initial guesses and chooses the ones that give the best correlation with the experimental data provided. However, you should carefully examine the obtained parameters. In some cases it might be advantageous to obtain hardening parameters for different numbers of backstresses before choosing the set of parameters.

Input File Usage

PLASTIC, HARDENING=COMBINED, DATA TYPE=HALF CYCLE, NUMBER BACKSTRESSES=n

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: Hardening: Combined, Data type: Half Cycle, Number of backstresses: n

Defining the kinematic hardening component by specifying test data from a stabilized cycle

Stress-strain data can be obtained from the stabilized cycle of a specimen that is subjected to symmetric strain cycles. A stabilized cycle is obtained by cycling the specimen over a fixed strain range $Δ ε$ until a steady-state condition is reached; that is, until the stress-strain curve no longer changes shape from one cycle to the next. Such a stabilized cycle is shown in Figure 10. Each data pair ( $σ_{i}, ε_{i}^{p l}$ ) must be specified with the strain axis shifted to $ε_{p}^{0}$ , so that

ε_{i}^{p l} = ε_{i} - \frac{σ_{i}}{E} - ε_{p}^{0},

and, thus, $ε_{1}^{p l} = 0$ .

Figure 10. Stress-strain data for a stabilized cycle.

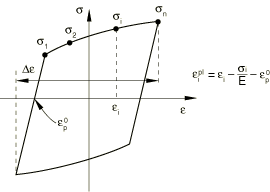
For each pair ( $σ_{i}, ε_{i}^{p l}$ ) values of $α_{i}$ ( $α_{i}$ is the overall backstress obtained by summing all the backstresses at this data point) are obtained from the test data as

α_{i} = σ_{i} - σ^{s},

where $σ^{s} = (σ_{1} + σ_{n}) / 2$ is the stabilized size of the yield surface.

Integration of the backstress evolution laws over this uniaxial strain cycle, with an exact match for the first data pair ( $σ_{1}, 0$ ), provides the expressions

α_{k} = \frac{C_{k}}{γ_{k}} (1 - e^{- γ_{k} ε^{p l}}) + α_{k, 1} e^{- γ_{k} ε^{p l}},

where $α_{k, 1}$ denotes the $k^{t h}$ backstress at the first data point (initial value of the $k^{t h}$ backstress). The above equations enable calibration of the parameters $C_{k}$ and $γ_{k}$ .

If the shapes of the stress-strain curves are significantly different for different strain ranges, you may want to obtain several calibrated values of $C_{k}$ and $γ_{k}$ . The tabular data of the stress-strain curves obtained at different strain ranges can be entered directly in Abaqus. Calibrated values corresponding to each strain range are reported in the data file, together with an averaged set of parameters, if model definition data are requested (see Controlling the amount of analysis input file processor information written to the data file). Abaqus will use the averaged set in the analysis. These parameters may have to be adjusted to improve the match to the test data at the strain range anticipated in the analysis.

The isotropic hardening component should be defined by specifying the equivalent stress defining the size of the yield surface at zero plastic strain, as well as the evolution of the equivalent stress as a function of equivalent plastic strain. If this component is not defined, Abaqus will assume that no cyclic hardening occurs so that the equivalent stress defining the size of the yield surface is constant and equal to $(σ_{1} + σ_{n}) / 2$ (or the average of these quantities over several strain ranges when more than one strain range is provided). Since this size corresponds to the size of a saturated cycle, this is unlikely to provide accurate predictions of actual behavior, particularly in the initial cycles.

Input File Usage

PLASTIC, HARDENING=COMBINED, DATA TYPE=STABILIZED, NUMBER BACKSTRESSES=n

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: Hardening: Combined, Data type: Stabilized, Number of backstresses: n

Multilinear kinematic hardening model

The multilinear kinematic hardening model can be calibrated using the test data obtained from a unidirectional tension or compression experiment. Abaqus expects you to provide the stress-plastic strain data pairs to define this multilinear behavior. The hardening modulus between the kth data point and the $(k + 1)$ th data point on the stress versus plastic strain curve, $H_{k},$ is determined from the relation

H_{k} = \frac{σ_{k + 1} - σ_{k}}{ε_{k + 1}^{p l} - ε_{k}^{p l}} .

The data should be such that the hardening modulus does not increase with plastic strain. The number of data points provided by the user determines the number of subvolumes, $N .$ The computational cost and memory requirements increase with $N .$ Therefore, the number of data points used to approximate the stress-plastic strain curve with a piecewise linear response should always be minimized.

You can provide several sets of data pairs as a function of temperature and/or field variable. However, you must ensure that the total number of data points or subvolumes corresponding to different temperatures and/or field variables is the same.

Input File Usage

PLASTIC, HARDENING=MULTILINEAR KINEMATIC

Abaqus/CAE Usage

Property module: material editor: MechanicalPlasticityPlastic: Hardening: Multilinear-Kinematic

Initial conditions

When we need to study the behavior of a material that has already been subjected to some hardening, Abaqus allows you to prescribe initial conditions for the equivalent plastic strain, ${\bar{ε}}^{p l}$ , and for the backstresses, $α_{k}$ , in the case of the linear kinematic hardening model and the nonlinear isotropic/kinematic hardening model. When the nonlinear isotropic/kinematic hardening model is used, the initial conditions for each backstress, $α_{k}$ , must satisfy the condition

\sqrt{\frac{3}{2} α_{k}^{d e v} : α_{k}^{d e v}} \leq C_{k} / γ_{k}

for the model to produce a kinematic hardening response. Abaqus allows the specification of initial backstresses that violate these conditions. However, in this case the response corresponding to the backstress for which the condition is violated produces kinematic softening response: the magnitude of the backstress decreases with plastic straining from its initial value to the saturation value. If the condition is violated for any of the backstresses, the overall response of the material is not guaranteed to produce kinematic hardening response. The initial condition for the backstress has no limitations when the linear kinematic hardening model is used.

You can specify the initial values of ${\bar{ε}}^{p l}$ and $α_{k}$ directly as initial conditions (see Initial conditions in Abaqus/Standard and Abaqus/Explicit).

Input File Usage

INITIAL CONDITIONS, TYPE=HARDENING, NUMBER BACKSTRESSES=n

Abaqus/CAE Usage

Load module: Create Predefined Field: Step: Initial, choose Mechanical for the Category and Hardening for the Types for Selected Step; Number of backstresses: n

User subroutine specification in Abaqus/Standard

For more complicated cases in Abaqus/Standard initial conditions can be defined through user subroutine HARDINI.

Input File Usage

INITIAL CONDITIONS, TYPE=HARDENING, USER, NUMBER BACKSTRESSES=n

Abaqus/CAE Usage

Load module: Create Predefined Field: Step: Initial, choose Mechanical for the Category and Hardening for the Types for Selected Step; Definition: User-defined, Number of backstresses: n

Elements

The linear kinematic hardening model and the nonlinear isotropic/kinematic hardening model can be used with elements in Abaqus/Standard that include mechanical behavior (elements that have displacement degrees of freedom), except some beam elements in space. Beam elements in space that include shear stress caused by torsion (i.e., not thin-walled, open sections) and do not include hoop stress (i.e., not PIPE elements) cannot be used with the nonlinear kinematic hardening model. In Abaqus/Explicit, the linear kinematic hardening model and the nonlinear isotropic/kinematic hardening model can be used with any elements that include mechanical behavior, with the exception of one-dimensional elements (beams, pipes, and trusses) when the models are used with the Hill yield surface. The multilinear kinematic hardening model can be used only in Abaqus/Standard with plane strain, generalized plane strain, axisymmetric, and three-dimensional solid (continuum) elements.

Output

In addition to the standard output identifiers available in Abaqus (Abaqus/Standard output variable identifiers and Abaqus/Explicit output variable identifiers), the following variables have special meaning for the kinematic hardening models:

ALPHA: Total kinematic hardening shift tensor components, $α_{i j} (i, j \leq 3)$ .
ALPHAk: $k^{t h}$ kinematic hardening shift tensor components ( $1 \leq k \leq 10$ ).
ALPHAN: All tensor components of all the kinematic hardening shift tensors, except the total shift tensor.
PEEQ: Equivalent plastic strain, ${\bar{ε}}^{p l} = {{\bar{ε}}^{p l} |}_{0} + \int_{0}^{t} \frac{σ : {\dot{ε}}^{p l} d t}{σ^{0}},$ where ${{\bar{ε}}^{p l} |}_{0}$ is the initial equivalent plastic strain (zero or user-specified; see Initial conditions).
PENER: Plastic work, defined as: $W^{p l} = \int_{0}^{t} σ : {\dot{ε}}^{p l} d t,$ . This quantity is not guaranteed to be monotonically increasing for kinematic hardening models. To get a quantity that is monotonically increasing, the plastic dissipation needs to be computed as: $W^{p l} = \int_{0}^{t} (σ - α) : {\dot{ε}}^{p l} d t$ . In Abaqus/Standard this quantity can be computed as a user-defined output variable in user subroutine UVARM.
YIELDS: Yield stress, $σ^{0}$ .