Slide line contact elements

Slide line elements:

can model the finite-sliding interaction between two deforming bodies when the sliding occurs along a line (“slide line”) that lies in a specific plane;
assume that tangential motions orthogonal to a slide line are zero or small (Abaqus/Standard treats such motions as being infinitesimal);
can be used with axisymmetric stress/displacement elements;
are recommended for specific applications, such as when a contact surface is the surface of a substructure or when CAXA or SAXA elements are involved in contact;
are available for first- and second-order elements; and
use the same “master-slave” concepts for enforcing contact constraints seen in surface-based contact.

For a general discussion of contact modeling, see Defining Contact Interactions.

The following topics are discussed:

Modeling contact between deformable bodies with slide lines
Local basis system for contact stresses and relative motions of the bodies
The master-slave concept for slide lines and slide line elements
Defining the slide line (master surface)
Defining slide line elements (slave surface)
Associating the slide line elements with a slide line
Defining the slide line element's section properties
Defining nondefault mechanical surface interactions with slide line elements
Obtaining the “maximum torque” that can be transmitted across axisymmetric slide lines

Modeling contact between deformable bodies with slide lines

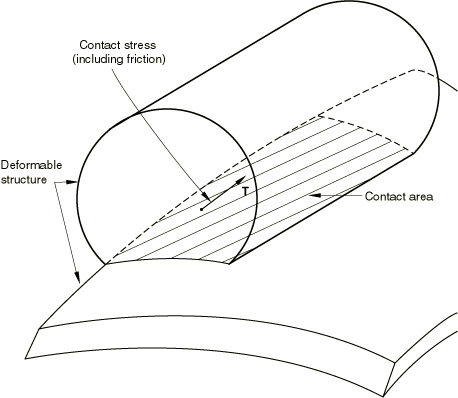
Determining the location of the areas of contact and the surface tractions between contacting structures are common goals of Abaqus simulations (see Figure 1). Slide lines and slide line contact elements can provide this information for simulations where both structures are deformable and the finite sliding of the structures occurs along well-defined lines.

Figure 1. Interaction between deformable structures.

Local basis system for contact stresses and relative motions of the bodies

Abaqus/Standard reports the contact stresses between the bodies and the relative motions of the bodies in a local basis system that is attached to the slide line surface. The local basis system is defined by the normal to the slide line, $n$ , and two orthogonal local tangent directions, $t_{1}$ and $t_{2}$ (see Figure 2).

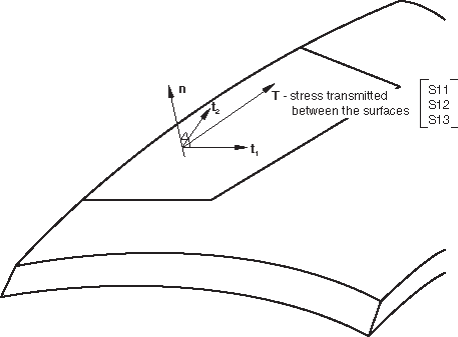
Figure 2. Local system for interface contact normal and shear traction.

Defining the local basis system

The sequence of the nodes forming the slide line defines the tangent, $t$ . The plane formed by the slide line normal, $n$ , and $t$ is called the contact plane. Abaqus/Standard defines the slide line normal as $n = s \times t$ (see Figure 3), where $s = (0, 0, 1)$ is the vector that is orthogonal to the contact plane.

As shown in Figure 3, a slide line is created using nodes i, j, k, …, p, which are specified in that order, thereby identifying the slide line tangent. Nodes I, J, K, …, N are the nodes of the slide line elements that are associated with this slide line. The slide line normal $n$ is defined by specifying $s$ , the normal to the contact plane.

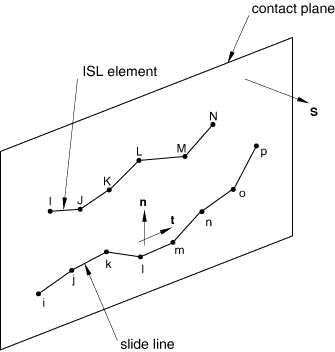
Figure 3. Defining the local basis for a slide line.

The tangent to the slide line coincides with the first local tangent direction, $t_{1}$ , of the local basis system. The second local tangent direction, $t_{2}$ , is in the opposite direction of $s$ .

The master-slave concept for slide lines and slide line elements

When creating a model that contains slide line elements, it is useful to remember that Abaqus/Standard uses a strict “master-slave” concept to enforce the contact constraints. The slide line contact elements form the “slave” surface. The nodes that you specify to define the slide line define the “master” surface. The nodes of the slide line contact elements are constrained not to penetrate the master surface.

The considerations for choosing the master and slave surfaces are the same regardless of whether surfaces or elements are used to define contact. The master surface should be chosen as the surface of the stiffer body if the materials are different or as the surface with the coarser mesh. If the materials and mesh density are the same on both surfaces, the choice is arbitrary.

Defining the slide line (master surface)

You can specify the nodes that make up the slide line, or they can be generated as described below. If you choose to specify the nodes directly, you must specify them in a sequence that defines a continuous slide line. The nodal sequence defines a tangent vector, $t$ , for the slide line. The slide line can be made up of linear or parabolic segments, depending on whether the model is made up of first-order or second-order elements. In either case convergence may be improved by smoothing the slide line.

Defining a linear slide line

When the surfaces of the bodies are meshed with first-order elements, define a slide line made up of linear element segments. As shown in Figure 4), nodes i, j, k, …, p are specified in that order, thereby identifying a slide line progressing from i through p. Nodes I, J, K, …, N are the nodes of the ISL-type elements that are associated with this slide line.

Input File Usage

SLIDE LINE, ELSET=element_set_name, TYPE=LINEAR
first node number, second node number, etc.

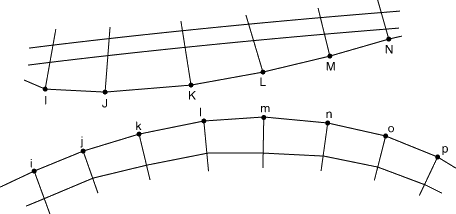
Figure 4. First-order (linear) slide line example.

Defining a parabolic slide line

When the surfaces of the bodies are meshed with second-order elements, define a slide line made up of second-order element segments. In this case the slide line should consist of an odd number of nodes. As shown in Figure 5, nodes i, j, k, …, u are specified in that order, thereby identifying a slide line progressing from i through u. Nodes I, J, K, …, O are the nodes of the ISL-type elements that are associated with this slide line.

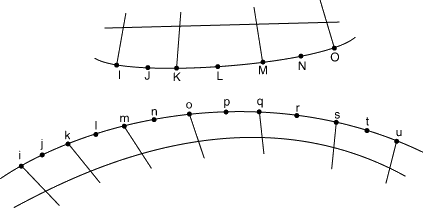
Figure 5. Second-order (parabolic) slide line example.

Input File Usage

SLIDE LINE, ELSET=element_set_name, TYPE=PARABOLIC
first node number, second node number, etc.

Generating the slide line nodes

Alternatively, you can indicate that the slide line nodes should be generated and specify only a first node number, a last node number, and an increment between node numbers.

Input File Usage

SLIDE LINE, ELSET=element_set_name, GENERATE
first node number, last node number, increment between node numbers

Smoothing the slide line

Convergence is often improved by smoothing the discontinuities in surface tangents between slide line segments, thereby providing a smoothly varying tangent along the slide line. For details about smoothing slide lines, see Contact formulations in Abaqus/Standard.

Defining slide line elements (slave surface)

Many finite-sliding contact simulations can use the surface-based contact approach, described in Defining Contact Interactions, to define the model. Axisymmetric stress/displacement and coupled temperature-displacement slide line elements are recommended only for specific applications, such as when a contact surface is the surface of a substructure or when CAXA or SAXA elements are involved in contact (see Contact modeling if asymmetric-axisymmetric elements are present).

The slide line contact elements define the slave surface. The contact area associated with each node on the slave surface is calculated using the current length of the slide line contact element and the constant “width” assigned to the element, which depends on the underlying finite elements.

Associating the slide line elements with a slide line

You must associate the slide line with a set of slide line contact elements. Details on defining slide lines are discussed below.

Input File Usage

SLIDE LINE, ELSET=element_set_name

Defining the slide line element's section properties

You must associate the section properties with a set of slide line elements.

There are no section data for axisymmetric slide line elements.

Input File Usage

INTERFACE, ELSET=element_set_name

Defining nondefault mechanical surface interactions with slide line elements

By default, Abaqus/Standard uses “hard,” frictionless contact with slide line elements. You can assign optional mechanical surface interaction models. The following mechanical surface interaction models are available:

Friction. See Frictional behavior for details.
Modified “hard” contact, softened contact, and viscous damping. See Contact pressure-overclosure relationships and Contact damping for details.

Obtaining the “maximum torque” that can be transmitted across axisymmetric slide lines

When modeling contact with slide lines with axisymmetric elements (type CAX and CGAX elements), Abaqus/Standard can calculate the maximum torque that can be transmitted across the axisymmetric slide lines. This capability is often of interest when modeling threaded connectors. The maximum torque, T, is defined as

T = \int \int r^{2} p d s d θ,

where p is the pressure transmitted across the interface, r is the radius to a point on the interface, and s is the current distance along the interface in the r–z plane. This definition of “torque” effectively assumes a friction coefficient of unity.

You can request that this torque output be written to the data (.dat) file. The data are provided for every slide line in the model. You can specify the output frequency to limit how often Abaqus/Standard writes this output to the data file. The default output frequency is 1.

For surface-based contact with axisymmetric elements, output variable CTRQ provides functionality similar to this torque output request (see About contact pairs in Abaqus/Standard).

Input File Usage

TORQUE PRINT, FREQUENCY=n