Electrical contact properties

Electrical conduction between two bodies:

is proportional to the difference in electric potentials across the interface;
is a function of the clearance between the surfaces;
can be a function of contact pressure;
can be a function of surface temperatures and/or predefined field variables on the surfaces; and
can generate heat at the interface.

See Coupled thermal-electrical analysis and Fully coupled thermal-electrical-structural analysis for details on coupled thermal-electrical and coupled thermal-electrical-structural analyses.

The following topics are discussed:

Including gap electrical conductance properties in a contact property definition
Modeling electrical conductance between surfaces
Modeling heat generated by electrical conduction between surfaces
Surface-based output variables for electrical contact property models

Including gap electrical conductance properties in a contact property definition

You can include electrical conductance properties in a contact property definition for surface-based contact.

Input File Usage

Use both of the following options:

SURFACE INTERACTION, NAME=name
GAP ELECTRICAL CONDUCTANCE

Abaqus/CAE Usage

Interaction module: contact property editor: ElectricalElectrical Conductance

Modeling electrical conductance between surfaces

Abaqus/Standard models the electrical current flowing between two surfaces as

J = σ_{g} (φ_{A} - φ_{B}),

where J is the electrical current density flowing across the interface from point A on one surface to point B on the other, $φ_{A}$ and $φ_{B}$ are the electrical potentials on opposite points on the surfaces, and $σ_{g}$ is the gap electrical conductance. Point A corresponds to a node on the slave surface of the contact pair. Point B is the point of the master surface in contact with point A.

You can provide the electrical conductance directly or in user subroutine GAPELECTR.

Defining σ_g directly

When the gap electrical conductance is defined directly, Abaqus/Standard assumes that

σ_{g} = σ_{g} (\bar{θ}, d, p, {\bar{f}}^{α}),

where

$\bar{θ} = \frac{1}{2} (θ_{A} + θ_{B})$: is the average of the surface temperatures at A and B,
d: is the clearance between A and B,
p: is the contact pressure transmitted across the interface between A and B, and
${\bar{f}}^{α} = \frac{1}{2} (f_{A}^{α} + f_{B}^{α})$: is the average of any predefined field variables at A and B.

Defining gap electrical conductance as a function of clearance

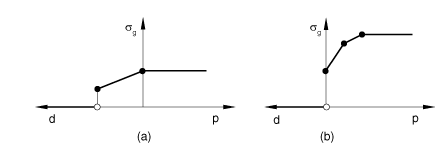
You can create a table of data defining the dependence of $σ_{g}$ on the variables listed above. The default in Abaqus is to make $σ_{g}$ a function of the clearance, d. When $σ_{g}$ is a function of gap clearance, d, the tabular data must start at zero clearance (closed gap) and define $σ_{g}$ as a function of the clearance. The value of $σ_{g}$ remains constant for clearances outside of the interval defined by the data points. If gap electrical conductance is not also defined as a function of contact pressure, $σ_{g}$ will remain constant at the zero clearance value for all pressures, as shown in Figure 1(a).

Figure 1. Examples of defining the gap electrical conductance as a function of clearance (a) or contact pressure (b).

Input File Usage

GAP ELECTRICAL CONDUCTANCE
 $σ_{g}$ ,  $d$ ,  $θ$

Abaqus/CAE Usage

Interaction module: contact property editor: ElectricalElectrical Conductance; Definition: Tabular; Use only clearance-dependency data

Defining gap electrical conductance as a function of contact pressure

You can define $σ_{g}$ as a function of the contact pressure, p. When $σ_{g}$ is a function of contact pressure at the interface, the tabular data must start at zero contact pressure (or, in the case of contact that can support a tensile force, the data point with the most negative pressure) and define $σ_{g}$ as p increases. The value of $σ_{g}$ remains constant for contact pressures outside of the interval defined by the data points. If gap electrical conductance is not also defined as a function of clearance, $σ_{g}$ is zero for all positive values of clearance and discontinuous at zero clearance, as shown in Figure 1(b).

Input File Usage

GAP ELECTRICAL CONDUCTANCE, PRESSURE
 $σ_{g}$ ,  $p$ ,  $θ$

Abaqus/CAE Usage

Interaction module: contact property editor: ElectricalElectrical Conductance; Definition: Tabular; Use only pressure-dependency data

Gap electrical conductance as a function of both clearance and contact pressure

You can define $σ_{g}$ to depend on both clearance and pressure. A discontinuity in $σ_{g}$ is allowed at $d = 0$ and $p = 0$ . Once contact occurs, the conductance is always evaluated based on the portion of the curve that defines the pressure dependence. The gap electrical conductance, $σ_{g}$ , remains constant for contact pressures outside of the interval defined by the data points. The pressure dependence of $σ_{g}$ is extended into the negative pressure region even if no data points with negative pressure are included.

Input File Usage

Use both of the following options:

GAP ELECTRICAL CONDUCTANCE
 $σ_{g}$ ,  $d$ ,  $θ$ 
GAP ELECTRICAL CONDUCTANCE, PRESSURE
 $σ_{g}$ ,  $p$ ,  $θ$

Abaqus/CAE Usage

Interaction module: contact property editor: ElectricalElectrical Conductance; Definition: Tabular; Use both clearance- and pressure-dependency data

Defining gap electrical conductance to be a function of predefined field variables

The gap electrical conductance can be dependent on any number of predefined field variables, ${\bar{f}}^{α}$ . By default, it is assumed that the electrical conductivity depends only on the surface separation and, possibly, on the average interface temperature.

Input File Usage

GAP ELECTRICAL CONDUCTANCE, DEPENDENCIES=n

Abaqus/CAE Usage

Interaction module: contact property editor: ElectricalElectrical Conductance; Definition: Tabular, Clearance Dependency and/or Pressure Dependency, Number of field variables: n

Defining σ_g using user subroutine GAPELECTR

When $σ_{g}$ is defined in user subroutine GAPELECTR, there is greater flexibility in specifying the dependencies of $σ_{g}$ than there is using direct tabular input. For example, it is no longer necessary to define $σ_{g}$ as a function of the average of the two surfaces' temperatures or field variables:

σ_{g} = σ_{g} (θ_{A}, θ_{B}, d, p, f_{A}^{α}, f_{B}^{α}) .

Input File Usage

GAP ELECTRICAL CONDUCTANCE, USER

Abaqus/CAE Usage

Interaction module: contact property editor: ElectricalElectrical Conductance; Definition: User-defined

Modeling heat generated by electrical conduction between surfaces

Abaqus/Standard can include the effect of heat generated by electrical conduction between surfaces in a coupled thermal-electrical and a fully coupled thermal-electrical-structural analysis. By default, all dissipated electrical energy is converted to heat and distributed equally between the two surfaces. You can modify the fraction of electrical energy that is released as heat and the distribution between the two surfaces; see Modeling heat generated by nonthermal surface interactions for details.

Surface-based output variables for electrical contact property models

Abaqus/Standard provides the following output variables related to the electrical interaction of surfaces:

ECD: Electric current per unit area leaving slave surface.
ECDA: ECD multiplied by the area associated with the slave node.
ECDT: Time integrated ECD.
ECDTA: Time integrated ECDA.

The values of these variables are always given at the nodes of the slave surface. They can be requested as surface output to the data, results, or output database files (see Surface output from Abaqus/Standard and Surface output in Abaqus/Standard and Abaqus/Explicit for details).

Contour plots of these variables can also be displayed in the Visualization module of Abaqus/CAE (Abaqus/Viewer).

Electrical contact properties

Including gap electrical conductance properties in a contact property definition

Modeling electrical conductance between surfaces

Defining σg directly

Defining gap electrical conductance as a function of clearance

Defining gap electrical conductance as a function of contact pressure

Gap electrical conductance as a function of both clearance and contact pressure

Defining gap electrical conductance to be a function of predefined field variables

Defining σg using user subroutine GAPELECTR

Modeling heat generated by electrical conduction between surfaces

Surface-based output variables for electrical contact property models

Defining σ_g directly

Defining σ_g using user subroutine GAPELECTR