Designing the mesh: partitioning and creating the mesh

You need to consider the type of element that will be used before you start building the mesh for a particular problem. For example, a suitable mesh design that uses quadratic elements may very well be unsuitable if you change to linear, reduced-integration elements.

This task shows you how to:

Partition the lug
Assign a global part seed and create the mesh

Context:

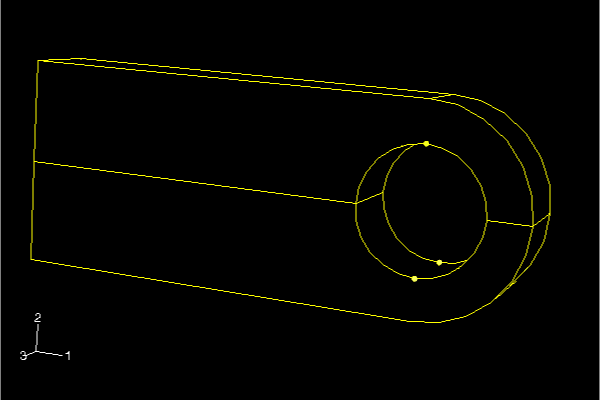
For this example use 20-node hexahedral elements with reduced integration (C3D20R). Once you have selected the element type, you can design the mesh for the connecting lug. The most important decision regarding the mesh design for this example is how many elements to use around the circumference of the lug's hole. A possible mesh for the connecting lug is shown in Figure 1.

Figure 1. Suggested mesh of C3D20R elements for the connecting lug model.

Another thing to consider when designing a mesh is the type of results you want from the simulation. The mesh in Figure 1 is rather coarse and, therefore, unlikely to yield accurate stresses. Four quadratic elements per 90° is the minimum number that should be considered for a problem such as this one; using twice that many is recommended to obtain reasonably accurate stress results. However, this mesh should be adequate to predict the overall level of deformation in the lug under the applied loads, which is what you were asked to determine. The influence of increasing the mesh density used in this simulation is discussed in Mesh convergence.

Abaqus/CAE offers a variety of meshing techniques to mesh models of different topologies. The different meshing techniques provide varying levels of automation and user control. The following three types of mesh generation techniques are available:

Structured meshing: Structured meshing applies preestablished mesh patterns to particular model topologies. Complex models must generally be partitioned into simpler regions to use this technique.
Swept meshing: Swept meshing extrudes an internally generated mesh along a sweep path or revolves it around an axis of revolution. Like structured meshing, swept meshing is limited to models with specific topologies and geometries.
Free meshing: The free meshing technique is the most flexible meshing technique. It uses no preestablished mesh patterns and can be applied to almost any model shape.
Bottom-up meshing: You use the bottom-up meshing technique to create a hexahedral or hex-dominated mesh on a solid region that is unmeshable or difficult to mesh using the automated top-down meshing techniques. Bottom-up meshing is a manual process that allows you to select the method and parameters that Abaqus/CAE uses to build up a solid mesh of hexahedral elements. Bottom-up meshing is not discussed in any of the examples in this guide.

When you enter the Mesh module, Abaqus/CAE color codes regions of the model according to the methods it will use to generate a mesh:

Green indicates that a region can be meshed using structured methods.
Yellow indicates that a region can be meshed using sweep methods.
Pink indicates that a region can be meshed using the free method.
Tan indicates that the region can be meshed using the bottom-up method.
Orange indicates that a region cannot be meshed using the default element shape assignment and must be partitioned further.

Dependent part instances are colored blue at the assembly level. You must switch to a part-level view to mesh a dependent part instance.

In this problem you will create a structured mesh. You will find that the model must first be partitioned further to use this mesh technique. After the partitions have been created, a global part seed will be assigned and the mesh will be created.

Partition the lug

In the Model Tree, expand the Lug item underneath the Parts container and double-click Mesh in the menu that appears.
The part is colored yellow initially, indicating that with the default set of mesh controls, a hexahedral mesh can be created only using a swept mesh technique. Additional cell partitions are required to permit structured meshing. Two partitions will be created. The first partition permits structured meshing to be used, and the second improves the overall quality of the mesh.

Note:
The Object field that appears in the context bar automatically displays the part so that you can partition the geometry directly within the Mesh module. The ability to switch between individual parts and the model assembly within the same module is available only in the Mesh module. This feature allows you to partition both dependent and independent part instances in the same module for the purpose of meshing. In all other modules, partitioning must be done strictly at the part level for dependent instances (as was done earlier when the pressure load was applied) or at the assembly level for independent part instances.
Partition both regions of the lug vertically by defining a cutting plane through the three points shown in Figure 2 (use ShiftClick to select both regions simultaneously).

Figure 2. First partition to permit structured meshing.
Select ToolsDatum from the main menu bar, and create a datum point 0.075 m from the left end of the lug (as shown in Figure 3) using the Offset from point method.

Figure 3. Second partition to improve the mesh quality.
Create the second vertical partition by using the Point & Normal method to define a cutting plane that is through the datum point you just created and normal to the centerline of the lug (as shown in Figure 3).

The partitioned lug appears as in Figure 4. After you have partitioned the lug, all part regions should be colored green, which (based on the current mesh controls) indicates structured hexahedral element meshing will be used everywhere.

Figure 4. Final partitioned lug.

Assign a global part seed and create the mesh

From the main menu bar, select SeedPart, and specify a target global element size of 0.007. Seeds appear on all the edges.
From the main menu bar, select MeshElement Type to choose the element type for the part. Because of the partitions you have created, the part is now composed of several regions.
1. Use the cursor to draw a box around the entire part and, thus, select all regions of the part. Click Done in the prompt area.
2. In the Element Type dialog box that appears, select the Standard element library, 3D Stress family, Quadratic geometric order, and Hex, Reduced integration element. Click OK to accept the choice of C3D20R as the element type.
Note:
If you are using the Abaqus Student Edition, using second-order elements with a global seed size of 0.007 results in a mesh that exceeds the model size limits of the product. Either use first-order elements (C3D8R) with a global seed size of 0.007 or second-order elements with a global seed size of 0.01.
From the main menu bar, select MeshPart. Click Yes in the prompt area to mesh the part instance.