Rivet forming | ||||||||||
|
| |||||||||
ProductsAbaqus/ExplicitAbaqus/CAE
Application description
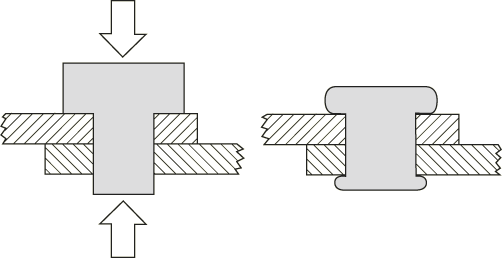
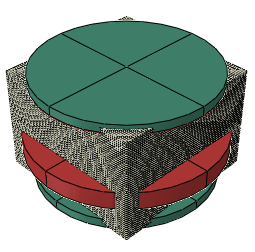
Rivets are a type of fastener designed to create permanent attachments between two or more sheets of material. A rivet design typically consists of a cylindrical body with two diameters: the smaller diameter is inserted through a hole in the overlapping sheets, then both ends of the rivet are compressed. The compression effectively expands the diameters of the rivet body, pinching the sheets of material between the two ends of the rivet (see Figure 1). Different rivet designs and applications will undergo different deformations, but the basic principle remains the same in all cases.
Three questions are of particular importance in this study:
Does the rivet deform appropriately during the forming process?
After the forming process, does the rivet retain enough strength to maintain a hold on the fastened materials?
Is the rivet installation tool capable of forming the rivet?
The displacements during the forming simulation indicate whether or not the rivet deforms appropriately. After the deformation, the strength of the rivet is based largely on its material properties; examining the equivalent plastic strain in the rivet gives some indication of potential damage or strength degradation in the material. To assess the effect of the rivet on the installation tool, reaction forces in the tool can be compared to known force capacities in standard installation tools.
Geometry
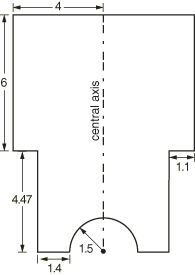
The rivet used in these analyses is a simple multidiameter cylinder, as described above. To aid the deformation of the smaller end of the rivet, a hemispherical portion is removed from the center of the cylinder. Figure 2 shows the dimensions of the rivet model.
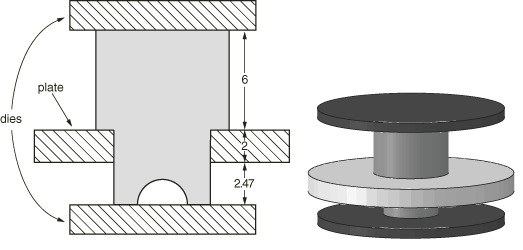
To simulate the forming, the rivet is placed in a hole at the center of a circular plate. Circular dies representing the installation tool are positioned at the top and bottom end of the rivet (see Figure 3).
Materials
The rivet in this model is composed of an elastic-plastic steel with a density of 7.85 × 10−9 t/mm3, Young's modulus of 2.1 × 105 N/mm2, Poisson's ratio of 0.266, and the onset of plastic yielding occuring at 3.0 × 105 N/mm2.
The plate and dies are assumed to be significantly harder than the rivet, and no deformation of these parts is expected.
Boundary conditions and loading
The forming process is simulated through the enforcement of displacement boundary conditions. The plate is constrained to a fixed location. The top die is displaced downward a distance of 3 mm, while at the same time the bottom die is displaced upward a distance of 2 mm.
Interactions
Contact interactions must be enforced between the rivet and all installation tool components; the deformation of the rivet depends on contact loads delivered through the displacement of the tool. The tool components never come into contact with each other, so interactions between the plate and dies can be neglected.
![]()
Abaqus modeling approaches and simulation techniques
The rivet forming simulation is conducted in Abaqus/Explicit using two fundamentally different element formulations. The traditional Lagrangian formulation generally offers accuracy and computational efficiency, but pure Lagrangian models tend to exhibit mesh distortion and an associated loss of accuracy when undergoing extreme deformations. The Eulerian formulation trades some accuracy of geometry and results for robustness in analyses involving very large deformations; in situations where the Lagragian formulation yields an unreliable solution or no solution at all, the Eulerian formulation can be used to obtain a reasonable solution.
Lagrangian and Eulerian elements can be combined in the same model using a technique known as coupled Eulerian-Lagrangian (CEL) analysis. In a CEL analysis bodies that undergo large deformations are meshed with Eulerian elements, while stiffer bodies in the model are meshed with more efficient Lagrangian elements.
The rivet forming analysis is performed using both a pure Lagrangian approach, in which the rivet, plate, and dies are all modeled with Lagrangian elements; and a coupled Eulerian-Lagrangian approach, in which the rivet is modeled with Eulerian elements while the plate and dies are modeled with Lagrangian elements.
Summary of analysis cases
| Case 1 | Pure Lagrangian rivet forming analysis. |
| Case 2 | Coupled Eulerian-Lagrangian (CEL) rivet forming analysis. |
The following sections detail some modeling techniques that are common to both analysis cases.
Analysis types
Both analysis cases are conducted using quasi-static explicit dynamic procedures. The forming takes place over the course of a single step lasting 1 ms.
Materials
The material for the rivet uses an isotropic hardening Mises plasticity model. The stress-strain data points used to define the plastic behavior are shown in Table 1.
Boundary conditions
In both analysis cases the plate and dies are modeled as Lagrangian bodies imposed with rigid body constraints. A boundary condition preventing displacements and rotations is imposed on the reference point for the plate body. Boundary conditions are also applied to each die reference point to prevent them from rotating or displacing, except in the vertical 3-direction: the boundary condition on the top reference point displaces it 3 mm in the negative 3-direction, and the boundary condition on the bottom reference point displaces it 2 mm in the positive 3-direction. The application of the boundary conditions is governed by an amplitude that ramps the displacement linearly from zero to full displacement over the course of 0.8 ms; the dies are then fixed in place for the final 0.2 ms of the analysis.
Constraints
As mentioned above, rigid body constraints are applied to the plate and two dies. These components are assumed to be significantly harder than the rivet, and they do not deform during the forming process. The rigid body constraints improve computational efficiency and allow the use of simple boundary conditions to initiate the forming.
Output requests
Field output is specifically requested for the equivalent plastic strains in the model (PEEQ). In addition, history output for the reaction force in the 3-direction (RF3) is requested at the reference point for each of the dies.
![]()
Pure Lagrangian analysis case
The first analysis case uses four Lagrangian bodies meshed from discrete geometric part instances. In the pure Lagrangian case the geometry of the model corresponds directly to the shapes of the parts being modeled, making the assembly process fairly intuitive.
Mesh design
The rivet is meshed with C3D8R elements using a global mesh seed of 0.25 mm (see Figure 4).
The plate and dies are also meshed with C3D8R elements, but the rigid body constraints applied to these parts makes the element selection somewhat arbitrary. Unmeshed analytical rigid surfaces could have been used to model the plate and dies, but rigid body constraints are used to maintain consistency with the CEL model.
Interactions
A general contact definition enforces contact interactions between all bodies in the model. A frictionless, hard contact model governs all interactions.
Solution controls
Although large deformations are expected in the analysis, no special solution controls or analysis techniques (such as adaptive meshing) are applied to the model, allowing a straightforward comparison between the pure Lagrangian model and the CEL model.
![]()
CEL analysis case
In the second analysis case the rivet is modeled using Eulerian elements. The plate and dies are still rigid bodies. The modeling approach in the CEL analysis has some distinct differences from the pure Lagrangian case.
Mesh design
In the Eulerian formulation the mesh does not generally correspond to the geometry of the part being modeled; rather, the placement of the material within the Eulerian mesh defines the geometry of the part. The Eulerian mesh does not deform or displace; only the materials within the mesh can move. Typically, the Eulerian mesh is an arbitrary collection of regular hexahedral elements that fully encompasses the region in which material may exist during the analysis.
In this example the Eulerian part is a rectangular prism measuring 17 × 17 × 11.5 mm meshed with EC3D8R elements. A global mesh seed of 0.25 mm dictates the element size.
This mesh does not define the geometry of the rivet; rather, the mesh defines the domain in which the rivet material can exist. The rivet geometry is defined by assigning steel material to a portion of this mesh corresponding to the shape of the rivet, as discussed in the Initial conditions section below. One strength of the Eulerian technique is the ability to define a regular, high-quality mesh independent of the geometry of the part being modeled.
It is important that the Eulerian mesh is large enough to contain the rivet material completely as it deforms; if material reaches the edge of the mesh, it flows out of the model and is lost to the simulation.
Initial conditions
The rivet geometry is defined using a material assignment initial condition on the Eulerian mesh. The material assignment specifies which elements in the mesh initially contain steel. Each element is designated a percentage (known as the volume fraction), which represents the portion of that element filled with steel. For partially filled elements Abaqus positions the material in the element such that it forms a continuous surface with the material in adjacent elements. The end result is a distribution of material in the mesh corresponding to the rivet geometry, as seen in Figure 5. You can use the view cut manager in the Visualization module of Abaqus/CAE to visualize the extent of a material within an Eulerian mesh, as discussed in Viewing output from Eulerian analyses.
The material assignment is created with the aid of the volume fraction tool in Abaqus/CAE. The volume fraction tool calculates the overlap between an Eulerian mesh and some reference geometric part. To use the volume fraction tool for this analysis case, the entire Lagrangian assembly (including the Lagrangian rivet) is copied from the previous analysis case and positioned inside the Eulerian mesh (see Figure 6). The Lagrangian rivet serves as the reference part, and the volume fraction tool creates a discrete field that associates each element in the Eulerian mesh with a volume fraction based on the amount of space occupied by the rivet within that element. This discrete field can then be used as the basis for a material assignment predefined field in Abaqus/CAE.
Interactions
A general contact definition enforces contact interactions between all rigid bodies and Eulerian materials in the model. General contact does not enforce contact between the rigid bodies and the Eulerian elements; the rigid bodies can pass unimpeded through the Eulerian mesh until they encounter a material within the mesh. As with the pure Lagrangian case, a frictionless, hard contact model governs all interactions.
It is generally not advisable to model Lagrangian-Eulerian contact near the boundary of the Eulerian mesh. The inflow or outflow of materials at the mesh boundary can lead to improper contact constraint enforcement. Therefore, the Eulerian mesh extends a few elements past the contact interfaces between the dies and the rivet.
General contact does not enforce interactions between analytical rigid surfaces and Eulerian materials, which is why the tool components must be modeled as Lagrangian parts with rigid body constraints.
Output requests
In addition to the field and history output requests used in the pure Lagrangian analysis case, the Eulerian volume fraction output variable (EVF) is requested as field output to visualize geometric results.
![]()
Discussion of results and comparison of cases
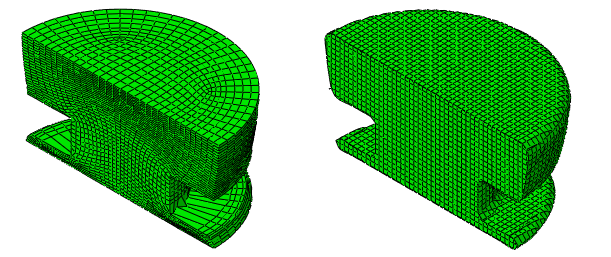
Figure 7 shows the deformed meshes for the pure Lagrangian and the CEL analysis cases. (To view the results of the CEL analysis, use the view cut manager as described in Viewing output from Eulerian analyses.) The pure Lagrangian analysis runs to completion, but the mesh becomes extremely distorted along the bottom of the rivet—results from such an irregular mesh may be unreliable. The Eulerian analysis exhibits a similar deformed shape but retains a high-quality, regular mesh.
Computational efficiency
In general, an Eulerian analysis is more expensive than a comparable Lagrangian analysis in terms of run times and file sizes. This performance tradeoff should be weighed against the benefits of Eulerian robustness for large deformations when choosing an analysis formulation.
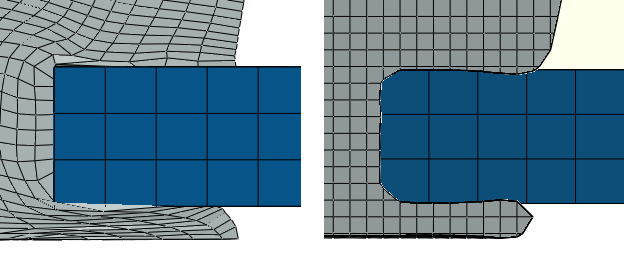
Difficulties with contact
Figure 8 shows the contact interface between the rivet and the plate for both the pure Lagrangian and the CEL cases. Both cases demonstrate some undesirable penetration of the rivet into the plate.
In the pure Lagrangian case the penetrations are a direct result of mesh distortion. As the rivet's facets spread out, there are fewer constraint points per given area, and portions of the facets are able to pass unconstrained into the plate surface. While the Lagrangian formulation is generally adept at simulating contact, a severely deformed mesh can cause noisy, inconsistent contact enforcement.
In the CEL case the penetrations result largely from approximations used to visualize Eulerian material. The boundary of an Eulerian material does not correspond to a discrete element face. As discussed previously, Abaqus determines the location of material in an Eulerian mesh based on a volume fraction within each element; the volume fractions are averaged and interpolated to calculate a smooth material surface during visualization. Therefore, the material boundary displayed in the Visualization module of Abaqus/CAE is an approximation based on numerical averaging, not geometric properties. The approximation causes the apparent penetrations at contact interfaces and explains why sharp corners in a Lagrangian model appear rounded in an Eulerian model. Despite the apparent penetrations, coupled Eulerian-Lagrangian contact does not suffer from the inconsistent constraint enforcement associated with pure Lagrangian mesh distortion, and contact between a solid Lagrangian body and an Eulerian material typically delivers reliable results.
In both analysis cases contact penetrations can be alleviated through the use of a finer mesh: smaller elements lead to reduced mesh distortion in the pure Lagrangian case, and additional elements provide additional sample points for more accurate volume fraction averaging in the Eulerian case.
Interpreting results
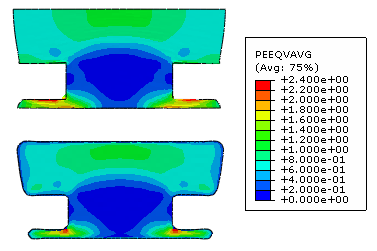
A contour plot of the equivalent plastic strains in a cross-section of the deformed rivet appears in Figure 9 for both analysis cases. The results are similar, but the regions of maximum plastic strain occur in slightly different areas. In the Eulerian rivet the peak strain occurs near the corner where the rivet meets the bottom of the plate; this region undergoes extreme bending and stretching during the forming. In the Lagrangian rivet the peak strain occurs in the elements with the most severe distortion. For small to moderate deformation, the Eulerian approach provides results that are comparable to the traditional Lagrangian approach (though at a higher computational cost); for large deformation the Eulerian results appear more reliable than the Lagrangian results.
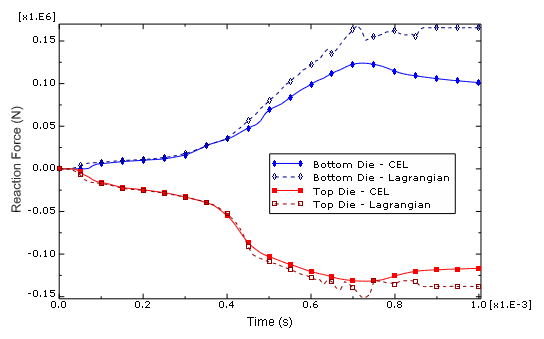
Figure 10 plots the reaction forces in both dies over the course of the forming process. The results for the two formulations are comparable during the first half of the analysis. However, the force plots for the pure Lagragian analysis case exhibit some noise during the latter half of the forming and subsequently diverge from the Eulerian force plots. The noise is likely the result of contact difficulties in the model (discussed above), which in turn lead to an uneven transfer of force between the tooling and the rivet. After 0.8 ms, when the dies have fully displaced, the forces in the Eulerian case exhibit some relaxation; the forces in the Lagrangian case remain steadily higher than the corresponding Eulerian forces due to the extreme deformation in the mesh.
![]()
Python scripts
- rivet_forming.py
-
Script to generate the pure Lagrangian and the CEL models in Abaqus/CAE.
![]()
Input files
- rivet_forming_lag.inp
-
Input file for the pure Lagrangian model.
- rivet_forming_cel.inp
-
Input file for the CEL model.
![]()
Tables
| Yield stress (N/mm2) | Plastic strain |
|---|---|
| 3.0 × 105 | 0 |
| 4.5 × 105 | 0.02 |
| 7.5 × 105 | 0.34 |
| 1.4 × 106 | 0.35 |
![]()
Figures