Connector functions for coupled behavior | ||
| ||
ProductsAbaqus/StandardAbaqus/ExplicitAbaqus/CAE
Defining derived components for connector elements
The definition of coupled behavior in connector elements beyond simple linear elasticity or damping often requires the definition of a resultant force involving several intrinsic (1 through 6) components or the definition of a “direction” not aligned with any of the intrinsic components. These user-defined resultants or directions are called derived components. The forces and motions associated with these derived components are functions of the forces and motions in the intrinsic relative components of motion in the connector element.
Consider the case of a SLOT connector for which frictional effects (see Connector friction behavior) are defined in the only available component of relative motion (the 1-direction). The two constraints enforced by this connection type will produce two reaction forces ( and ), as shown in Figure 1. Both forces generate friction in the 1-direction in a coupled fashion.
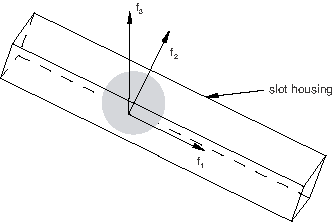
A reasonable estimate for the resulting contact force is
where is the collection of connector forces and moments in the intrinsic components. The function can be specified as a derived component.
Resultant forces that can be defined as derived components may take more complicated forms. Consider a BUSHING connection type for which a tensile (Mode I) damage mechanism with failure is to be specified in the 1-direction. You may wish to include the effects of the axial force and of the resultant of the “flexural” moments and in defining an overall resultant force in the axial direction upon which damage initiation (and failure) can be triggered, as shown in Figure 2.
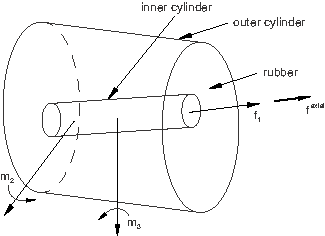
One choice would be to define the resultant axial force as
where is a geometric factor relating translations to rotations with units of one over length. The function can be specified as a derived component.
A derived component can also be interpreted as a user-specified direction that is not aligned with the connector component directions. For example, if the motion-based damage with failure criterion in a CARTESIAN connection with elastic behavior does not align with the intrinsic component directions, the damage criterion can be defined in terms of a derived component representing a different direction, as shown in Figure 3.
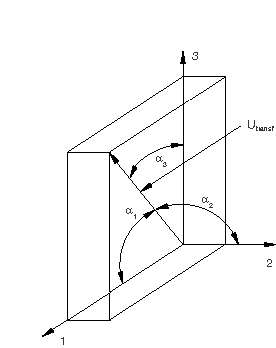
One possible choice for the direction could be
where is the collection of connector relative motions in the components and , , and can be interpreted as direction cosines (, , ). The function can be specified as a derived component.
Functional form of the derived component
The functional form of a derived component in Abaqus is quite general; you specify its exact form. The derived component is specified as a sum of terms
where is a generic name for the connector intrinsic component values (such as forces, , or motions, ), is the term in the sum, and is the number of terms. The appropriate component values for are selected depending on the context in which the derived component is used. is also a summation of several contributions and can take one of the following three forms:
a norm (-type)
a direct sum (-type)
a Macauley sum (-type)
where is the term's sign (plus or minus), are scaling factors, is the component of , and is the Macauley bracket (). In general, the units of the scaling factors depend on the context. In most cases they are either dimensionless, have units of length, or have units of one over length. The scaling factors should be chosen such that all the terms in the resulting derived component have the same units, and these units must be consistent with the use of the derived component later on in a connector potential or connector contact force.
Defining a derived component with only one term (NT = 1)
Connector derived components are identified by the names given to them. If one term () is sufficient to define the derived component g, specify only one connector derived component definition.
Input File Usage
CONNECTOR DERIVED COMPONENT, NAME=derived_component_name
Abaqus/CAE Usage
Connector derived component names are not supported in Abaqus/CAE; you define the individual derived component terms.
Use the following input to define a connector derived component term for a friction-generating user-defined contact force:
Interaction module: connector section editor: : Friction model: User-defined, Contact Force, Specify component: Derived component, click to display the derived component editor: click Add and select components
Use the following input to define a connector derived component term as an intermediate result in a connector potential function:
Interaction module: connector section editor: , , or : potential contribution editors: Specify derived component, click to display the derived component editor: click Add and select components
Defining a derived component containing multiple terms (NT > 1)
If several terms (, , etc.) are needed in the overall definition of the derived component g, you must define the individual terms.
Input File Usage
You must specify connector derived component definitions with the same name to define the individual terms. All definitions with the same name will be summed together to produce the desired derived component g. See the spot weld example below for an illustration.
CONNECTOR DERIVED COMPONENT, NAME=derived_component_name CONNECTOR DERIVED COMPONENT, NAME=derived_component_name ...
Abaqus/CAE Usage
Connector derived component names are not supported in Abaqus/CAE; you define the individual derived component terms.
Interaction module: derived component editor: click Add and select components. Repeat, adding terms as necessary.Specifying a term in the derived component as a norm
By default, a derived component term is computed as the square root of the sum of the squares of each intrinsic component contribution. If the term has only one contribution (), the norm has the same meaning as the absolute value.
Input File Usage
CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, OPERATOR=NORM (default)
For example, the following input can be used to define the component discussed above:
CONNECTOR DERIVED COMPONENT, NAME=axial 1 1.0, ** CONNECTOR DERIVED COMPONENT, NAME=axial 5, 6 , **
The axial derived component is .
Abaqus/CAE Usage
Interaction module: derived component editor: Add: Term operator: Square root of sum of squares
Specifying a term in the derived component as a direct sum
Alternatively, you can choose to compute a derived component term as the direct sum of the intrinsic component contributions.
Input File Usage
CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, OPERATOR=SUM
For example, the following input can be used to define the component discussed above:
CONNECTOR DERIVED COMPONENT, NAME=transf, OPERATOR=SUM 1, 2, 3 , , **
The transf derived component is .
Abaqus/CAE Usage
Interaction module: derived component editor: Add: Term operator: Direct sum
Specifying a term in the derived component as a Macauley sum
Alternatively, you can choose to compute a derived component term as the Macauley sum of the intrinsic component contributions.
Input File Usage
CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, OPERATOR=MACAULEY SUM
For example, the following input can be used to define the first term of the normal component of the force () in the spotweld example discussed below:
CONNECTOR DERIVED COMPONENT, NAME=normal, OPERATOR=MACAULEY SUM 3 1.0 **
Abaqus/CAE Usage
Interaction module: derived component editor: Add: Term operator: Macauley sum
Specifying the sign of a term
You can specify whether the sign of a derived component term should be positive or negative.
Input File Usage
Use one of the following options:
CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, SIGN=POSITIVE (default) CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, SIGN=NEGATIVE
Abaqus/CAE Usage
Interaction module: derived component editor: Add: Overall term sign: Positive or Negative
Defining the derived component contributions to depend on local directions
The scaling factors used in the definition of the derived component can depend on the relative positions or constitutive displacements/rotations in several component directions, as described in Defining nonlinear connector behavior properties to depend on relative positions or constitutive displacements/rotations. See the first example in Connector friction behavior for an illustration.
Input File Usage
Use the following option to define a connector derived component that depends on components of relative position:
CONNECTOR DERIVED COMPONENT, INDEPENDENT COMPONENTS=POSITION
Use the following option to define a connector derived component that depends on components of constitutive displacements or rotations:
CONNECTOR DERIVED COMPONENT, INDEPENDENT COMPONENTS=CONSTITUTIVE MOTION
Abaqus/CAE Usage
Interaction module: derived component editor: Add: Use local directions: Independent position components or Independent constitutive motion components
Requirements for constructing a derived component used in plasticity or friction definitions
When a derived component is used to construct the yield function for a plasticity or friction definition, the following simple requirements must be satisfied:
All terms of a derived component must be of a compatible type (see Functional form of the derived component); norm-type terms (-type) cannot be mixed with direct sum-type terms (-type) in the same derived component definition but can be mixed with Macauley sum-type terms (-type).
If all terms are norm-type terms, the sign of each term must be positive (the default).
If is greater than 1, the associated functions (potentials) in which the derived component is used may become non-smooth. More precisely, the normal to the hyper-surface defined by the potential may experience sudden changes in direction at certain locations. In these cases, Abaqus will automatically smooth-out the defined functions by slightly changing the derived component functional definition. These changes should be transparent to the user as the results of the analysis will change only by a small margin.
Example: spot weld
The spot weld shown in Figure 4 is subjected to loading in the F-direction.
The connector chosen to model the spot weld has six available components of relative motion: three translations (components 1–3) and three rotations (components 4–6). You have chosen this connection type because you are modeling a general deformation state. However, you would like to define inelastic behavior in the connection in terms of a normal and a shear force, as shown in Figure 5, since experimental data are available in this format.
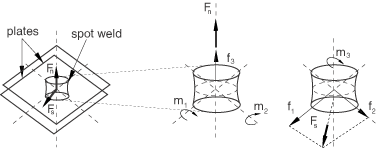
Therefore, you want to derive the normal and shear components of the force, for example, as follows:
In these equations and have units of length; their interpretation is relatively straightforward if you consider the spot weld as a short beam with the axis along the spot weld axis (3-direction). If the average cross-section area of the spot weld is A and the beam's second moment of inertia about one of the in-plane axes is (or ), can be interpreted as the square root of the ratio (or ). Furthermore, if the cross-section is considered to be circular, becomes equal to a fraction of the spot weld radius. In all cases can be taken to be .
The reasoning above for the interpretation of the calibration constants in the equations is only a suggestion. In general, any combination of constants that would lead to good comparisons with other results (experimental, analytical, etc.) is equally valuable.
To define , you would specify the following two connector derived component definitions, each with the same name:
PARAMETER =30.68 A=19.63 =sqrt() = CONNECTOR DERIVED COMPONENT, NAME=normal, OPERATOR=MACAULEY SUM 3 1.0 CONNECTOR DERIVED COMPONENT, NAME=normal 4, 5 ,
The symbols denote that is specified using a parameter definition. The normal force derived component is defined as the sum of two terms, . The first connector derived component defines the first term , while the second defines the second term .
Similarly, to define , you would specify the following two connector derived component definitions for the component shear:
CONNECTOR DERIVED COMPONENT, NAME=shear 6 CONNECTOR DERIVED COMPONENT, NAME=shear 1, 2 1.0, 1.0
![]()
Defining connector potentials
Connector potentials are user-defined mathematical functions that represent yield surfaces, limiting surfaces, or magnitude measures in the space spanned by the components of relative motion in the connector. The functions can be quadratic, general elliptical, or maximum norms. The connector potential does not define a connector behavior by itself; instead, it is used to define the following coupled connector behaviors:
friction,
plasticity, or
damage.
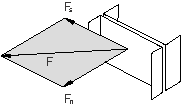
Consider the case of a SLIDE-PLANE connection in which frictional sliding occurs in the connection plane, as shown in Figure 6.
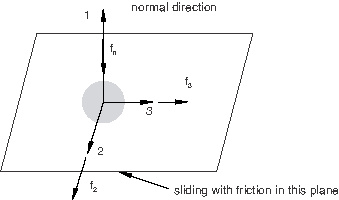
The function governing the stick-slip frictional behavior (see Connector friction behavior) can be written as
where is the connector potential defining the pseudo-yield function (the magnitude of the frictional tangential tractions in the connector in a direction tangent to the connection plane on which contact occurs), is the friction-producing normal (contact) force, and is the friction coefficient. Frictional stick occurs if , and sliding occurs if . In this case the potential can be defined as the magnitude of the frictional tangential tractions,
Connector potentials can also be useful in defining connector damage with a force-based coupled damage initiation criterion. For example, in a connection type with six available components of relative motion you could define a potential
Damage (with failure) can be initiated when the value of the potential is greater than a user-specified limiting value (usually 1.0). The units of the and coefficients must be consistent with the units of the final product. For example, if the intended units of are newtons, the coefficients are dimensionless while the coefficients have units of length.
Connector potentials can take more complicated forms. Assume that coupled plasticity is to be defined in a spot weld, in which case a plastic yield criterion can be defined as
where is the connector potential defining the yield function and is the yield force/moment. The potential could be defined as
where and could be the named derived components normal and shear defined in the example in Defining derived components for connector elements above. If has units of force and and also have units of force, and are dimensionless.
Input File Usage
Abaqus/CAE Usage
Use the following input to define connector potentials for friction behavior:
Interaction module: connector section editor: : Friction model: User-defined, Slip direction: Compute using force potential, Force Potential
Use the following input to define connector potentials for plasticity behavior:
Interaction module: connector section editor: : Coupling: Coupled, Force Potential
Use the following input to define connector potentials for damage behavior:
Interaction module: connector section editor: : Coupling: Coupled, Initiation Potential or Evolution Potential
Functional form of the potential
The functional form of the potential in Abaqus is quite general; you specify its exact form. The potential is specified as one of the following direct functions of several contributions:
- a quadratic form
- a general elliptical form
- a maximum form
where is a generic name for the connector intrinsic component values (such as forces, , or motions, ), is the contribution to the potential, is the number of contributions, and are positive numbers (defaults 2.0, ), and is the overall sign of the contribution (1.0 – default, or −1.0). The appropriate component values for are selected depending on the context in which the potential is used in. The positive exponents (, ) and the sign should be chosen such that the contribution yields a real number.
is a direct function of either an intrinsic connector component (1 through 6) or a derived connector component. Since derived components are ultimately a function of intrinsic components (see Defining derived components for connector elements), the contribution is ultimately a function of . is defined as
where
is the function used to generate the contribution:
absolute value (default, ),
Macauley bracket (), or
identity (X);
is the value of the identified component (intrinsic or derived);
is a shift factor (default 0.0); and
is a scaling factor (default 1.0).
The function can be the identity function only if . The units of the various coefficients in the equations above depend on the context in which the potential is used. In most cases the coefficients in the equations above are either dimensionless, have units of length, or have units of one over length. In all cases you must be careful in defining potentials for which the units are consistent.
Defining the potential as a quadratic or general elliptical form
To define a general elliptical form of the potential, you must specify the inverse of the overall exponent, . You can also define the exponents if they are different from the default value, which is the specified value of .
Input File Usage
To define a quadratic form of the potential, you can omit specifying since its default value is 2.0. Use the following option:
CONNECTOR POTENTIAL component name or number, , , , , ...
Use the following option to define a general elliptical form of the potential:
CONNECTOR POTENTIAL, OPERATOR=SUM, EXPONENT= component name or number, , , , , ...
Each data line defines one contribution to the potential, . The function can be ABS (absolute value and the default), MACAULEY (Macauley bracket), or NONE (identity).
Abaqus/CAE Usage
Interaction module: connector section editor: friction, plasticity, or damage behavior option: Force Potential, Initiation Potential, or Evolution Potential: Operator: Sum, Exponent: 2 (for quadratic form) or (for elliptical form), select Add and enter data for the potential contribution. Repeat, adding contributions as necessary.
Defining the potential as a maximum form
Alternatively, you can define the potential as a maximum form.
Input File Usage
CONNECTOR POTENTIAL, OPERATOR=MAX component name or number, , , , , ...
Each data line defines one contribution to the potential, . The function can be ABS (absolute value and the default), MACAULEY (Macauley bracket), or NONE (identity).
Abaqus/CAE Usage
Interaction module: connector section editor: friction, plasticity, or damage behavior option: Force Potential, Initiation Potential, or Evolution Potential: Operator: Maximum, select Add and enter data for the potential contribution. Repeat, adding contributions as necessary.
Requirements for constructing a potential used in plasticity or friction definitions
The connector potential, , can be defined using intrinsic components of relative motion, derived components, or both. A particular contribution to the potential may be one of the following two types:
A norm-type contribution () defined using the absolute value or the Macauley bracket functions or using a combination of norm-type and Macauley sum-type derived components (see Requirements for constructing a derived component used in plasticity or friction definitions) with any of the available functions.
A sum-type contribution () defined using an intrinsic component of relative motion or a derived component of type (see Requirements for constructing a derived component used in plasticity or friction definitions) together with the identity function.
When used in the context of connector plasticity or connector friction, the potential must be constructed such that the following requirements are satisfied:
All contributions to the potential must be of the same type. Mixed and contributions are not allowed in the same potential definition.
If all terms are -type terms, the sign of each term must be positive (the default).
The positive numbers and cannot be smaller than 1.0 and must be equal (the default).
Example: spot weld
Referring to the spot weld shown in Figure 5 and the yield function defined above, you would define this potential using the derived components normal and shear with the following input:
PARAMETER =0.02 =0.05 =1.5 CONNECTOR POTENTIAL, EXPONENT= normal, , , MACAULEY shear, , , ABS
![]()
Output
The Abaqus/Explicit output variables available for connectors are listed in Abaqus/Explicit output variable identifiers. The following variables (available only in Abaqus/Explicit ) are of particular interest when defining connector functions for coupled behavior:
- CDERF
Connector derived force/moment with the connector derived component name appended to the output variable. If the connector derived component is used with connector plasticity, connector friction, and connector damage initiation (type force), the derived components used to form the potential represent forces and this quantity is available for both field and history output. If connector friction is used with contact force, the derived components are not used to form a potential, and the derived force is in fact the connector normal forceCNF (which is available for connector history output.)
- CDERU
Connector derived displacement/rotation with the connector derived component name appended to the output variable. If the connector derived component is used with motion type for the connector damage initiation and connector damage evolution, the derived components to form the potential represent displacements and this quantity is available for both field and history output.