Spherical cavity in an infinite medium

This example of an internally pressurized spherical cavity in an infinite medium was analyzed by Marques and Owen (1983) and compares results obtained using infinite elements to results obtained with finite elements only, assuming fixed or free boundary conditions at the truncated end of the mesh. In addition, it investigates the performance of meshes with different degrees of refinement compared to the analytical solution provided by Hill (1950).

The following topics are discussed:

ProductsAbaqus/Standard

Problem description

In consistent units the radius of the cavity is 1.0, and an internal pressure of 750 is applied. The material is isotropic, linear elastic, with Young's modulus 107 and Poisson's ratio 0.33.

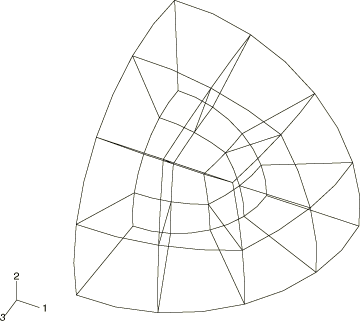
Using three orthogonal planes of symmetry, only one-eighth of the configuration needs to be analyzed. The finite element meshes are made up of layers of 12 C3D20R elements, as shown in Figure 1. Two basic meshes of three layers of elements are used: one where the layers are defined by the radial positions 1, 2, 3, 4 and the other where the layers are defined by the radial positions 1, 2, 4, 8. In each case the outermost nodes are considered to be either fixed or free. This results in four different finite element meshes that we label as follows:

  • F4FX – outer radius = 4, outer nodes fixed

  • F4FR – outer radius = 4, outer nodes free

  • F8FX – outer radius = 8, outer nodes fixed

  • F8FR – outer radius = 8, outer nodes free

Two coupled finite/infinite element meshes are used. First, we take an F8 mesh and replace the outer layer of finite elements by a layer of CIN3D12R elements. We label this mesh I4, the digit 4 indicating the radius at which the finite and infinite elements are coupled. Second, we use a mesh with a single layer of finite elements between radial values 1 and 2 and coupled to it a layer of CIN3D12R elements. This mesh is labeled I2. To test the use of substructures in problems involving coupled finite/infinite element meshes, the I2 mesh is also solved using substructuring with the entire model treated as a single substructure.

Results and discussion

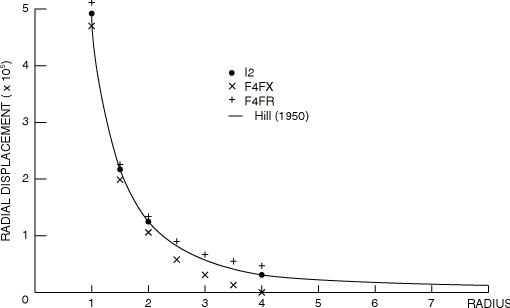
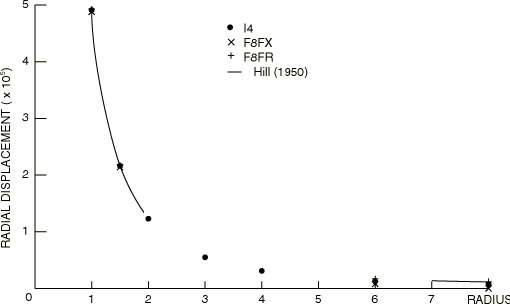
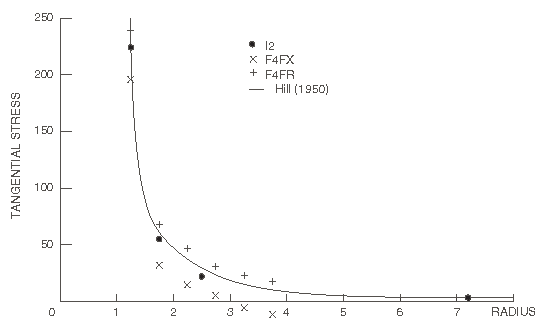
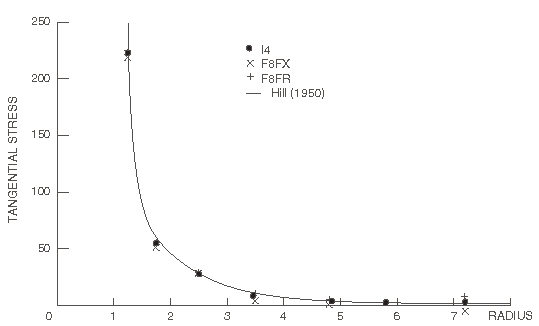
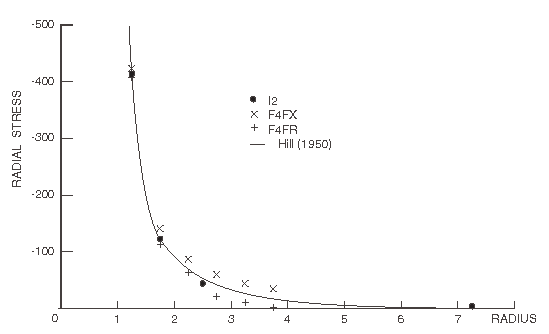
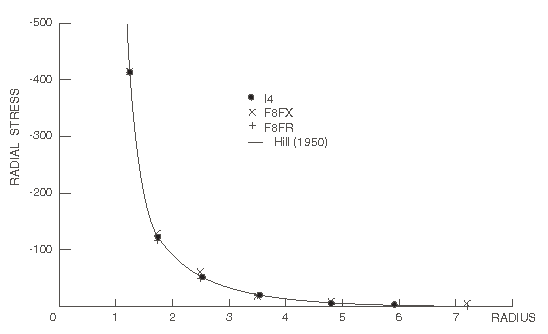
Hill's analytical solution for this problem is shown in Figure 2 and Figure 3 (radial displacements) and Figure 4, Figure 5, Figure 6, and Figure 7 (tangential and radial stresses). The results obtained with finite element meshes F4FX and F4FR and with the finite/infinite element mesh I2 are compared to the analytical solution in Figure 2, Figure 4, and Figure 6. We see that models F4FX and F4FR provide upper and lower bound solutions, while the infinite element result agrees almost exactly with the theory. Even this very crude finite/infinite element mesh (with only a single layer of finite elements) provides accurate results for this simple case. Figure 3, Figure 5, and Figure 7 show the results obtained with meshes F8FX, F8FR, and I4: again the infinite element results are in almost exact agreement with the analytical solution, while the better finite element representations also provide results that are close to the analytical solution. The results from the substructure analysis match the results that are obtained when substructures are not used.

Input files

sphericalcavinfmed_i2.inp

Model I2.

sphericalcavinfmed_i4.inp

Model I4.

sphericalcavinfmed_f4fx.inp

Model F4FX.

sphericalcavinfmed_f8fx.inp

Model F8FX.

sphericalcavinfmed_i2_sub.inp

Model I2 using substructuring.

sphericalcavinfmed_i2_sub_gen1.inp

Substructure generation referenced by the analysis sphericalcavinfmed_i2_sub.inp.

sphericalcavinfmed_i2_cin3d18r.inp

Model I2 using CIN3D18R elements.

sphericalcavinfmed_i4_cin3d18r.inp

Model I4 using CIN3D18R elements.

References

  1. Hill,  R., The Mathematical Theory of Plasticity, Oxford University Press, 1950.
  2. Marques,  J. M. M. C.,  and D. R. J. Owen, “Infinite Elements in Quasi–Static Materially Nonlinear Problems,” University of Wales Report, Swansea, 1983.

Figures

Figure 1. Typical element layer.

Figure 2. Radial displacement results—meshes F4FX, F4FR, and I2.

Figure 3. Radial displacement results—meshes F8FX, F8FR, and I4.

Figure 4. Tangential stress distribution—meshes F4FX, F4FR, and I2.

Figure 5. Tangential stress distribution—meshes F8FX, F8FR, and I4.

Figure 6. Radial stress distribution—meshes F4FX, F4FR, and I2.

Figure 7. Radial stress distribution—meshes F8FX, F8FR, and I4.