About Variance Reduction Techniques | ||||
|
| |||
The number of simulations necessary for Simple Random Sampling is usually more than desirable and often more than practical. Other sampling techniques have been developed to reduce the sample size (number of simulations) without sacrificing the quality of the statistical description of the behavior of the system. These techniques, called variance reduction techniques, reduce the variance of the statistical estimates derived from the Monte Carlo simulation data. As a result, the error in estimates is reduced (estimates from multiple simulations are more consistent). Alternatively, fewer points are needed with variance reduction techniques to obtain error or confidence levels similar to those obtained through simple random sampling. The descriptive sampling and Sobol sampling variance reduction techniques are available in Isight.
Descriptive Sampling
Descriptive sampling (Saliby, 1990) is available for the Monte Carlo component. In this technique the space defined by each random variable is divided into subsets of equal probability, and the analysis is performed with each subset of each random variable only once (each subset of one random variable is combined with only one subset of each other random variable).
Descriptive sampling technique is similar to the Latin Hypercube DOE technique (see Latin Hypercube Technique) and is best described through illustration as in the figure below for two random variables in standard space (U-space). Each row and column in the discretized two-variable space is sampled only once in random order. The cloud of points generated using Simple Random Sampling is shown below for comparison.
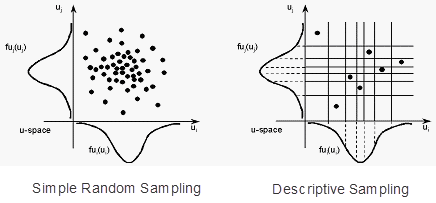
![]()
Sobol Sampling
Sobol sampling is a quasi-random sequence of numbers that are more uniformly distributed than both simple random sampling and descriptive sampling. In other words, samples obtained using Sobol's sequences exhibit a probability density function that is closer to the true density function (as shown in the image below, Press et al, 1992).
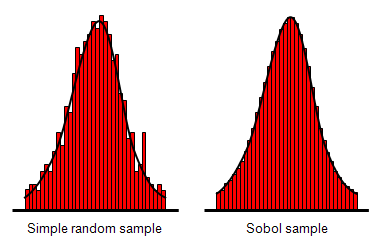
A Sobol sequence generates numbers as binary fractions of appropriate length from a set of special binary fractions. Refer to Press et al. (1992) and Antonov and Saleev (1979) for a detailed description of the number theoretic method for generating Sobol sequences.