Computing the stress components

Linearized stress components are computed using user-defined sections traversing a finite element model structure.

The following topics are discussed:

Three-dimensional structures
Axisymmetric structures

Three-dimensional structures

The membrane values of the stress components are computed using the following equation:

σ^{m} = \frac{1}{t} \underset{- t / 2}{\int^{t / 2}} σ d x,

where

$σ^{m}$ is the membrane value of stress,
t is the thickness of the section,
$σ$ is the stress along the path, and
x is the coordinate along the path.

The linear bending values of the stress components are computed using the following equations:

σ_{B}^{b} = - σ {}^{b}{_{A}} = \frac{6}{t^{2}} \underset{- t / 2}{\int^{t / 2}} σ \cdot x \cdot d x,

where $σ {}^{b}{_{A}}$ and $σ_{B}^{b}$ are the bending values of the stress at point A and point B (the endpoints of the section; see Figure 1).

Figure 1. Recommended stress paths.

The integration is performed numerically. Assuming the path between point A and point B is divided uniformly into n intervals, the integrals are evaluated as follows:

σ^{m} = \frac{1}{2 n} \overset{n}{\sum_{j = 1}} (σ_{j} + σ_{j + 1})

and

σ_{A}^{b} = - \frac{3}{n t} \overset{n}{\sum_{j = 1}} (σ_{j} x_{j} + σ_{j + 1} x_{j + 1}),

where $σ_{j}$ is the stress at point j along the path.

Axisymmetric structures

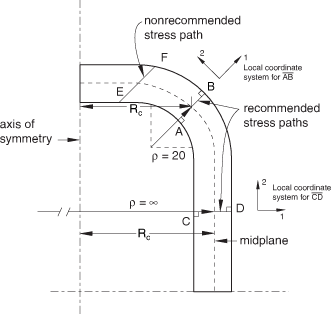
The derivation of the above equations is similar for the axisymmetric case, except for the fact that the neutral axis is shifted radially outward. Separate expressions are obtained for the stresses in the thickness, meridional, and hoop directions. In Abaqus/CAE these are represented as local directions 1, 2, and 3, respectively (see Figure 2).

Figure 2. Stress directions.

Meridional stress

The meridional stresses are computed using the following relations. The meridional force per unit circumferential length is

F_{y} = \underset{- t / 2}{\int^{t / 2}} σ_{y} \frac{R}{R_{c}} d x,

where

$σ_{y}$ is the stress in the meridional direction,
R is the radius of the point being integrated, and
$R_{c} = \frac{1}{2} (R_{A} + R_{B})$ is the mean circumferential radius.

The meridional membrane stress $σ_{y}^{m}$ is obtained by dividing $F_{y}$ through the thickness:

σ_{y}^{m} = \frac{F_{y}}{t} = \frac{1}{R_{c} t} \underset{- t / 2}{\int^{t / 2}} σ_{y} R d x .

The numerical scheme used to compute the meridional membrane stress is

σ_{y}^{m} = \frac{1}{2 n R_{c}} \underset{j = 1}{\sum^{n}} (σ_{y j} R_{j} + σ_{y (j + 1)} R_{j + 1}),

where

$σ_{y j}$ is the meridional stress component at point j along the path and
$R_{j}$ is the radius at point j along the path.

To compute the meridional bending stresses, we first need to compute the distance from the center surface to the neutral surface for meridional bending. That distance, $x_{f}$ , is equal to

x_{f} = \frac{t^{2} \cdot \cos ϕ}{12 \cdot R_{c}},

where $ϕ$ is the angle between the thickness direction and the radial direction.

The meridional bending moment per unit circumferential length is defined as

M_{y} = \underset{- t / 2}{\int^{t / 2}} (x - x_{f}) σ_{y} \frac{R}{R_{c}} d x,

and the moment of inertia for meridional bending is given by

I_{y} = \underset{- t / 2}{\int^{t / 2}} {(x - x_{f})}^{2} \frac{R}{R_{c}} d x = \frac{1}{12} t^{3} - x_{f}^{2} t .

Hence, the meridional bending stresses at the endpoints A and B are obtained with

σ_{y A}^{b} = \frac{M_{y} (x_{A} - x_{f})}{I_{y}}, σ_{y B}^{b} = \frac{M_{y} (x_{B} - x_{f})}{I_{y}} .

The numerical scheme used to compute the meridional bending moment is

M_{y} = \frac{t}{2 n R_{c}} \overset{n}{\sum_{j = 1}} [σ_{y j} R_{j} (x_{j} - x_{f}) + σ_{y (j + 1)} R_{j + 1} (x_{j + 1} - x_{f})] .

Hoop stress

The hoop membrane stress $σ_{h}^{m}$ is obtained with

σ_{h}^{m} = \frac{F_{h}}{t} = \frac{1}{t} \underset{- t / 2}{\int^{t / 2}} σ_{h} (1 + \frac{x}{ρ}) d x,

where

$σ_{h}$ is the hoop stress and
$ρ$ is the radius of curvature of the midsurface of the section in the meridional plane.

The hoop bending stresses at the endpoints are obtained using the relations

σ_{h A}^{b} = \frac{M_{h} (x_{A} - x_{h})}{I_{h}}, σ_{h B}^{b} = \frac{M_{h} (x_{B} - x_{h})}{I_{h}},

where

x_{h} = \frac{t^{2}}{12 ρ}

is the distance from the center surface to the neutral surface for hoop bending,

M_{h} = \underset{- t / 2}{\int^{t / 2}} (x - x_{h}) σ_{h} (1 + \frac{x}{ρ}) d x

is the hoop bending moment per unit meridional length, and

I_{h} = \int_{- t / 2}^{t / 2} {(x - x_{h})}^{2} (1 + \frac{x}{ρ}) d x = \frac{1}{12} t^{3} - x_{h}^{2} t

is the moment of inertia for circumferential bending.

The numerical scheme to compute the circumferential membrane stress is

σ_{h}^{m} = \frac{1}{2 n ρ} \overset{n}{\sum_{j = 1}} [σ_{h j} (ρ + x_{j}) + σ_{h (j + 1)} (ρ + x_{j + 1})],

and the bending moment is computed with the summation

M_{h} = \frac{t}{2 n ρ} \sum [σ_{h (j)} (ρ + x_{j}) (x_{j} - x_{h}) + σ_{h (j + 1)} (ρ + x_{j + 1}) (x_{j + 1} - x_{h})] .

Thickness stress

The thickness stress does not transfer any forces or moments. Typically, the stress arises due to applied external pressures and thermal expansion effects, and there is no obvious preferred method for determining membrane and bending stresses. Hence, we choose the thickness membrane stress as the average thickness stress:

σ_{x}^{m} = \frac{1}{t} \underset{- t / 2}{\int^{t / 2}} σ_{x} d x = \frac{1}{2 n} \overset{n}{\sum_{j = 1}} (σ_{x (j)} + σ_{x (j + 1)}) .

We choose the thickness bending stress such that the sum of the thickness membrane and bending stresses at the endpoints A and B is equal to the total stress at these points:

σ_{x A}^{b} = σ_{x A} - σ_{x}^{m}, σ_{x B}^{b} = σ_{x B} - σ_{x}^{m},

and interpolate the bending stress linearly between these values. This is a reasonable assumption, since the thickness surface stresses are determined by the applied pressure and should not have a strong peak stress contribution.

Shear stress

The membrane shear stress in the meridional plane is computed in the same way as the meridional membrane stress:

σ_{x y}^{m} = \frac{1}{t} \underset{- t / 2}{\int^{t / 2}} σ_{x y} \frac{R}{R_{c}} d x,

where $σ_{x y}$ is the shear stress along the path.

The shear stress distribution is assumed to be parabolic and equal to zero at the ends. Hence, the bending shear stresses are set to 0.0. The numerical scheme used to compute the membrane shear stress is:

σ_{x y}^{m} = \frac{1}{2 n R_{c}} \underset{j = 1}{\sum^{n}} (σ_{x y (j)} R_{j} + σ_{x y (j + 1)} R_{j + 1}) .