Stress intensity factor extraction

In general, the J-integral for a given problem can be written as

where $I,II,III$ correspond to $1,2,3$ when indicating the components of B. We define the J-integral for an auxiliary, pure Mode I, crack-tip field with stress intensity factor $k_I$ as

Superimposing the auxiliary field onto the actual field yields

Since the terms not involving $K_I$ or $k_I$ in $J_{tot}^I$ and J are equal, the interaction integral can be defined as

If the calculations are repeated for Mode $II$ and Mode $III$, a linear system of equations results:

If the $k_{\alpha }$ are assigned unit values, the solution of the above equations leads to

where ${\mathbf{J}}_{int}={\lfloor J_{int}^I,J_{int}^{II},J_{int}^{III}\rfloor }^T$ The calculation of this integral is discussed next.

Based on the definition of the J-integral, the interaction integrals $J_{int}^{\alpha }$ can be expressed as

with ${\mathbf{M}}^{\alpha }$ given as

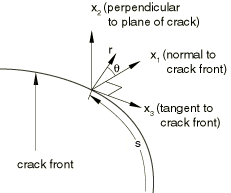
The subscript $aux$ represents three auxiliary pure Mode I, Mode II, and Mode III crack-tip fields for $\alpha =I,II,III$, respectively. $\mathrm{\Gamma }$ is a contour that lies in the normal plane at position s along the crack front, beginning on the bottom crack surface and ending on the top surface (see Figure 1). The limit $\mathrm{\Gamma }\to 0$ indicates that $\mathrm{\Gamma }$ shrinks onto the crack tip.

Following the domain integral procedure used in Abaqus/Standard for calculating the J-integral, we define an interaction integral for a virtual crack advance $\lambda \left(s\right)$:

where L denotes the crack front under consideration; $dA$ is a surface element on a vanishingly small tubular surface enclosing the crack tip (i.e., $dA=dsd\mathrm{\Gamma }$); $\mathbf{n}$ is the outward normal to $dA$; and $\mathbf{q}$ is the local direction of virtual crack propagation. The integral ${\overline{J}}_{int}^{\alpha }$ can be calculated by the same domain integral method as that used for calculating the J-integral.

To obtain $J_{int}^{\alpha }$ at each node set P along the crack front line, $\lambda$ is discretized with the same interpolation functions as those used in the finite elements along the crack front:

where ${\lambda }^Q=1$ at the node set P and all other ${\lambda }^Q$ are zero. The result is substituted into the expression for ${\overline{J}}_{int}^{\alpha }$. Finally, the interaction integral value at each node set P along the crack front can be calculated as