Small-strain shell elements in Abaqus/Explicit

The small-strain shell elements in Abaqus/Explicit use a Mindlin-Reissner type of flexural theory that includes transverse shear. The elements are based on a corotational velocity-strain formulation described by Belytschko et al. (1984, 1992). A corotational finite element formulation reduces the complexities of nonlinear mechanics by embedding a local coordinate system in each element at the sampling point of that element. By expressing the element kinematics in a local coordinate frame, the number of computations is reduced substantially. Therefore, the corotational velocity-strain formulation provides significant speed advantages in explicit time integration software, where element computations can dominate during the overall solution process.

The following topics are discussed:

Corotational coordinate system
Velocity strain formulation
Small-strain element S4RS
Small-strain element S4RSW
Small-strain element S3RS
Hourglass control

Corotational coordinate system

The geometry of the shell is defined by its reference surface, which is determined by the nodal coordinates of the element. The embedded element corotational coordinate system, $\hat{x}$ , is tangent to the reference surface and rotates with the element. This embedded corotational coordinate system serves as a local coordinate system and is constructed as follows:

For the quadrilateral element the local coordinate ${\hat{x}}_{1}$ is coincident with the line connecting the midpoints of sides, $r_{a c}$ , as shown in Figure 1.

Figure 1. Local coordinate system for small-strain quadrilateral and triangular shell elements.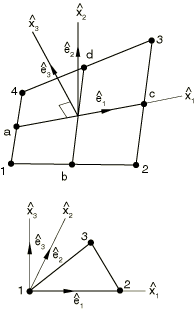

The ${\hat{x}}_{1}$ – ${\hat{x}}_{2}$ plane is defined to pass through this line normal to the cross product $r_{a c} \times r_{b d}$ .
For the triangular element the local coordinate ${\hat{x}}_{1}$ is coincident with the side connecting nodes 1 and 2 as shown in Figure 1. The ${\hat{x}}_{1}$ – ${\hat{x}}_{2}$ plane coincides with the plane of the element.

For notational purposes the corotational coordinate system is defined by a triad ${\hat{e}}_{i}$ , and any vector or tensor whose components are expressed in this system will bear a superposed “hat.”

Although the corotational coordinate system described here is used in the actual element computations, this system is transparent to the user. All reported stresses, strains, and other tensorial quantities for these shell elements are defined with respect to the coordinate system described in Finite-strain shell element formulation.

Velocity strain formulation

The velocity of any point in the shell reference surface is given in terms of the discrete nodal velocity with the bilinear isoparametric shape functions $N^{I} (ξ_{α})$ as

v^{m} = N^{I} (ξ_{α}) v^{I},

θ = N^{I} (ξ_{α}) θ^{I},

where $v^{I}$ and $θ^{I}$ are the nodal translation and rotation velocity, respectively. The functions $N^{I} (ξ_{α})$ are $C_{\circ}$ continuous, and $ξ_{α}$ are nonorthogonal, nondistance measuring parametric coordinates. Here Greek subscripts range from 1 to 2, and uppercase Roman superscripts denote the nodes of an element. A standard summation convention is used for repeated superscripts and subscripts except where noted otherwise.

In the Mindlin-Reissner theory of plates and shells, the velocity of any point in the shell is defined by the velocity of the reference surface, ${\hat{v}}^{m}$ , and the angular velocity vector, $\hat{θ}$ , as

\hat{v} = {\hat{v}}^{m} - {\hat{x}}_{3} {\hat{e}}_{3} \times \hat{θ},

where $\times$ denotes the vector cross product and ${\hat{x}}_{3}$ is the distance in the normal direction through the thickness of the shell element. The corotational components of the velocity strain (rate of deformation) are given by

{\hat{d}}_{i j} = \frac{1}{2} (\frac{\partial {\hat{v}}_{i}}{\partial {\hat{x}}_{1} j} + \frac{\partial {\hat{v}}_{j}}{\partial {\hat{x}}_{1} i}),

which allows us to write each velocity strain component in terms of the nodal translational and rotational velocities:

{\hat{d}}_{1} = \frac{\partial {\hat{v}}_{1}^{m}}{\partial {\hat{x}}_{1}} + {\hat{x}}_{3} \frac{\partial {\hat{θ}}_{1}}{\partial {\hat{x}}_{1}},

{\hat{d}}_{2} = \frac{\partial {\hat{v}}_{2}^{m}}{\partial {\hat{x}}_{2}} - {\hat{x}}_{3} \frac{\partial {\hat{θ}}_{2}}{\partial {\hat{x}}_{2}},

{\hat{d}}_{12} = \frac{\partial {\hat{v}}_{1}^{m}}{\partial {\hat{x}}_{2}} + \frac{\partial {\hat{v}}_{2}^{m}}{\partial {\hat{x}}_{1}} + {\hat{x}}_{3} (\frac{\partial {\hat{θ}}_{2}}{\partial {\hat{x}}_{2}} - \frac{\partial {\hat{θ}}_{1}}{\partial {\hat{x}}_{1}}),

{\hat{d}}_{23} = \frac{\partial {\hat{v}}_{3}^{m}}{\partial {\hat{x}}_{2}} - {\hat{θ}}_{1},

{\hat{d}}_{13} = \frac{\partial {\hat{v}}_{3}^{m}}{\partial {\hat{x}}_{1}} + {\hat{θ}}_{2} .

Small-strain element S4RS

The S4RS element is based on Belytschko et al. (1984). By using one-point quadrature at the center of the element—i.e., at $ξ_{α}$ =0—we obtain the gradient operator

{\begin{matrix} B_{1}^{I} \\ B_{2}^{I} \end{matrix}} = \frac{1}{2 A} [\begin{matrix} {\hat{y}}_{2} - {\hat{y}}_{4} & {\hat{y}}_{3} - {\hat{y}}_{1} & {\hat{y}}_{4} - {\hat{y}}_{2} & {\hat{y}}_{1} - {\hat{y}}_{3} \\ {\hat{x}}_{4} - {\hat{x}}_{2} & {\hat{x}}_{1} - {\hat{x}}_{3} & {\hat{x}}_{2} - {\hat{x}}_{4} & {\hat{x}}_{3} - {\hat{x}}_{1} \end{matrix}] .

The velocity strain can then be expressed as

{\hat{d}}_{1} = B_{1}^{I} {\hat{v}}_{1}^{I} + {\hat{x}}_{3} B_{1}^{I} {\hat{θ}}_{2}^{I},

{\hat{d}}_{2} = B_{2}^{I} {\hat{v}}_{2}^{I} - {\hat{x}}_{3} B_{2}^{I} {\hat{θ}}_{1}^{I},

2 {\hat{d}}_{12} = B_{2}^{I} {\hat{v}}_{1}^{I} + B_{1}^{I} {\hat{v}}_{2}^{I} + {\hat{x}}_{3} (B_{2}^{I} {\hat{θ}}_{2}^{I} - B_{1}^{I} {\hat{θ}}_{1}^{I}),

2 {\hat{d}}_{13} = B_{1}^{I} {\hat{v}}_{3}^{I} + \frac{1}{4} S^{I} {\hat{θ}}_{2}^{I},

2 {\hat{d}}_{23} = B_{2}^{I} {\hat{v}}_{3}^{I} - \frac{1}{4} S^{I} {\hat{θ}}_{1}^{I},

where

S^{I} = [1, 1, 1, 1] .

The local nodal forces and moments are computed in terms of the section force and moment resultants by

{\hat{f}}_{1}^{I} = A (B_{1}^{I} {\hat{f}}_{1} + B_{2}^{I} {\hat{f}}_{12}),

{\hat{f}}_{2}^{I} = A (B_{2}^{I} {\hat{f}}_{2} + B_{1}^{I} {\hat{f}}_{12}),

{\hat{f}}_{3}^{I} = κ A (B_{1}^{I} {\hat{f}}_{13} + B_{2}^{I} {\hat{f}}_{23}),

{\hat{m}}_{1}^{I} = A (B_{2}^{I} {\hat{m}}_{2} + B_{1}^{I} {\hat{m}}_{12} - \frac{κ}{4} S^{I} {\hat{f}}_{23}),

{\hat{m}}_{2}^{I} = - A (B_{1}^{I} {\hat{m}}_{1} + B_{2}^{I} {\hat{m}}_{12} - \frac{κ}{4} S^{I} {\hat{f}}_{13}),

{\hat{m}}_{3}^{I} = 0.

The section force and moment resultants are given by

{\hat{f}}_{α β} = \int_{h} {\hat{σ}}_{α β} d \hat{z},

{\hat{m}}_{α β} = - \int_{h} \hat{z} {\hat{σ}}_{α β} d \hat{z},

where A is the area of the element, h is the thickness, and ${\hat{σ}}_{α β}$ are the Cauchy stresses computed in the corotational system from the velocity strain and the applicable constitutive model. Although $κ$ is the shear factor in classical Mindlin-Reissner plate theory, it is used here as a penalty parameter to enforce the Kirchhoff normality condition as the shell becomes thin.

Small-strain element S4RSW

The major objective in the development of the S4RS element was to obtain a convergent, stable element with the minimum number of computations. Because of the emphasis on speed, a few simplifications were made in formulating the equations for the S4RS element. Although the S4RS element performs very well in most practical applications, it has two known shortcomings:

It can perform poorly when warped, and in particular, it does not solve the twisted beam problem correctly.
It does not pass the bending patch test in the thin plate limit.

In the S4RSW element additional terms are added to the strain-displacement equations to eliminate the first shortcoming, and a shear projection is used in the calculation of the transverse shear to address the second shortcoming. The components of velocity strain in the S4RSW element are given in Belytschko et al. (1992) as

{\hat{d}}_{1} = B_{1}^{I} {\hat{v}}_{1}^{I} + {\hat{x}}_{3} (B_{1}^{c I} {\hat{v}}_{1}^{I} + B_{1}^{I} {\dot{p}}_{1}^{I}),

{\hat{d}}_{2} = B_{2}^{I} {\hat{v}}_{2}^{I} + {\hat{x}}_{3} (B_{2}^{c I} {\hat{v}}_{2}^{I} + B_{2}^{I} {\dot{p}}_{2}^{I}),

2 {\hat{d}}_{12} = B_{2}^{I} {\hat{v}}_{1}^{I} + B_{1}^{I} {\hat{v}}_{2}^{I} + {\hat{x}}_{3} (B_{1}^{c I} {\hat{v}}_{2}^{I} + B_{2}^{c I} {\hat{v}}_{1}^{I} + B_{1}^{I} {\dot{p}}_{2}^{I} + B_{2}^{I} {\dot{p}}_{1}^{I}),

where $p_{α}^{I}$ is the pseudonormal at node I and $B_{α}^{c I}$ is given by

{\begin{matrix} B_{1}^{c I} \\ B_{2}^{c I} \end{matrix}} = \frac{2 z_{γ}}{A^{2}} [\begin{matrix} {\hat{x}}_{1} - {\hat{x}}_{3} & {\hat{x}}_{4} - {\hat{x}}_{2} & {\hat{x}}_{3} - {\hat{x}}_{1} & {\hat{x}}_{2} - {\hat{x}}_{4} \\ {\hat{y}}_{1} - {\hat{y}}_{3} & {\hat{y}}_{4} - {\hat{y}}_{2} & {\hat{y}}_{3} - {\hat{y}}_{1} & {\hat{y}}_{2} - {\hat{y}}_{4} \end{matrix}],

where

z_{γ} = γ^{I} {\hat{x}}_{3}^{I},

γ^{I} = \frac{1}{4} [h^{I} - B_{α}^{I} {\hat{x}}_{α}^{J} h^{J}],

h^{I} = [+ 1, - 1, + 1, - 1] .

The pseudonormal $p_{α}^{I}$ represents a nodal normal local to a particular element found by taking the vector cross product of the adjacent element sides.

The components of the transverse shear velocity strain are given by

{\hat{γ}}_{13} = N^{I} (ξ_{α}) {\bar{θ}}_{2}^{I},

{\hat{γ}}_{23} = - N^{I} (ξ_{α}) {\bar{θ}}_{1}^{I},

where nodal rotational components ${\bar{θ}}_{1}^{I}$ and ${\bar{θ}}_{2}^{I}$ are based on a projection and a transformation. Consider three adjacent local element nodes K, I, and J as shown in Figure 2. Outward facing vectors $e_{n}^{K}$ and $e_{n}^{I}$ are constructed perpendicular to element sides $K I$ and $I J$ , respectively. In addition, they are tangent to the reference surface at the midsides.

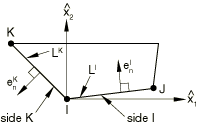
Figure 2. Vector and edge definition for shear projection in the element S4RSW.

The angular velocity $θ_{n}^{I}$ about outward facing vector $e_{n}^{I}$ is then given by a nodal projection

θ_{n}^{I} = \frac{1}{2} (θ_{n I}^{I} + θ_{n I}^{J}) + \frac{1}{L^{I}} ({\hat{v}}_{3}^{J} - {\hat{v}}_{3}^{I}), no sum on I,

where $θ_{n I}^{I}$ is the rotational velocity at node I about $e_{n}^{I}$ , $θ_{n I}^{J}$ is the rotational velocity at node J about $e_{n}^{I}$ , and $L^{I}$ is the length of side I. Finally, the nodal rotational components ${\bar{θ}}_{1}^{I}$ and ${\bar{θ}}_{2}^{I}$ required for the transverse shear velocity strain are given by the transformation

{\bar{θ}}_{1}^{I} = (e_{n}^{I} \cdot {\hat{e}}_{1}) θ_{n}^{I} + (e_{n}^{K} \cdot {\hat{e}}_{1}) θ_{n}^{K},

{\bar{θ}}_{2}^{I} = (e_{n}^{I} \cdot {\hat{e}}_{2}) θ_{n}^{I} + (e_{n}^{K} \cdot {\hat{e}}_{2}) θ_{n}^{K} .

Evaluating the resulting forms for the transverse shear at the centroidal quadrature point gives

2 {\hat{d}}_{13} = B_{11}^{s I} {\hat{v}}_{3}^{I} + B_{12}^{s I} {\hat{θ}}_{1}^{I} + B_{13}^{s I} {\hat{θ}}_{2}^{I},

2 {\hat{d}}_{13} = B_{21}^{s I} {\hat{v}}_{3}^{I} + B_{22}^{s I} {\hat{θ}}_{1}^{I} + B_{23}^{s I} {\hat{θ}}_{2}^{I},

where

{\begin{matrix} B_{1 i}^{s I} \\ B_{2 i}^{s I} \end{matrix}} = \frac{1}{4} [\begin{matrix} 2 ({\bar{x}}_{1}^{J I} - {\bar{x}}_{1}^{I K}) & {\hat{x}}_{1}^{J I} {\bar{x}}_{2}^{J I} + {\hat{x}}_{1}^{I K} {\bar{x}}_{2}^{I K} & - ({\hat{x}}_{1}^{J I} {\bar{x}}_{1}^{J I} + {\hat{x}}_{1}^{I K} {\bar{x}}_{1}^{I K}) \\ 2 ({\bar{x}}_{2}^{J I} - {\bar{x}}_{2}^{I K}) & {\hat{x}}_{2}^{J I} {\bar{x}}_{2}^{J I} + {\hat{x}}_{2}^{I K} {\bar{x}}_{2}^{I K} & - ({\hat{x}}_{1}^{J I} {\bar{x}}_{2}^{J I} + {\hat{x}}_{1}^{I K} {\bar{x}}_{2}^{I K}) \end{matrix}] no sum on I, J, and K,

{\hat{x}}_{α}^{J I} = {\hat{x}}_{α}^{J} - {\hat{x}}_{α}^{I}

and

{\bar{x}}_{α}^{J I} = \frac{{\hat{x}}_{α}^{J I}}{{(L^{I})}^{2}}, no sum on I .

The local nodal forces and moments are then given in terms of the section resultant forces and moments by

{\hat{f}}_{1}^{I} = A (B_{1}^{I} {\hat{f}}_{1} + B_{2}^{I} {\hat{f}}_{12} + B_{1}^{c I} {\hat{m}}_{1} + B_{2}^{c I} {\hat{m}}_{12}),

{\hat{f}}_{2}^{I} = A (B_{2}^{I} {\hat{f}}_{2} + B_{1}^{I} {\hat{f}}_{12} + B_{2}^{c I} {\hat{m}}_{2} + B_{1}^{c I} {\hat{m}}_{12}),

{\hat{f}}_{3}^{I} = κ A (B_{11}^{s I} {\hat{f}}_{13} + B_{21}^{s I} {\hat{f}}_{23}),

{\hat{m}}_{1}^{I} = A (B_{2}^{I} {\hat{m}}_{2} + B_{1}^{I} {\hat{m}}_{12} + κ (B_{12}^{s I} {\hat{f}}_{13} + B_{22}^{s I} {\hat{f}}_{23})),

{\hat{m}}_{2}^{I} = - A (B_{1}^{I} {\hat{m}}_{1} + B_{2}^{I} {\hat{m}}_{12} + κ (B_{13}^{s I} {\hat{f}}_{13} + B_{23}^{s I} {\hat{f}}_{23})),

{\hat{m}}_{3}^{I} = 0.

Small-strain element S3RS

The triangular shell element formulation is similar to that of the S4RS element and is based on Kennedy et al. (1986). This element is not subject to zero energy modes inherent in quadrilateral element formulations.

The velocity strain is computed as in the S4RS element except that the gradient operator is given by

{\begin{matrix} B_{1}^{I} \\ B_{2}^{I} \end{matrix}} = \frac{1}{2 A} [\begin{matrix} - {\hat{y}}_{3} & {\hat{y}}_{3} & 0 \\ {\hat{x}}_{3} - {\hat{x}}_{2} & - {\hat{x}}_{3} & {\hat{x}}_{2} \end{matrix}] .

The local nodal forces and moments for the triangular shell can be expressed in terms of section resultant forces and moments as

{\hat{f}}_{1}^{I} = A (B_{1}^{I} {\hat{f}}_{1} + B_{2}^{I} {\hat{f}}_{12}),

{\hat{f}}_{2}^{I} = A (B_{2}^{I} {\hat{f}}_{2} + B_{1}^{I} {\hat{f}}_{12}),

{\hat{m}}_{1}^{I} = A (B_{2}^{I} {\hat{m}}_{2} + B_{1}^{I} {\hat{m}}_{12} - \frac{κ}{3} {\hat{f}}_{23}),

{\hat{m}}_{2}^{I} = - A (B_{1}^{I} {\hat{m}}_{1} + B_{2}^{I} {\hat{m}}_{12} - \frac{κ}{3} {\hat{f}}_{13}),

{\hat{m}}_{3}^{I} = 0.

The ${\hat{x}}_{3}$ -components of the nodal forces are obtained by successively solving the following equations:

{\hat{m}}_{1}^{1} + {\hat{m}}_{1}^{2} + {\hat{m}}_{1}^{3} + {\hat{x}}_{3} {\hat{f}}_{3}^{3} = 0,

{\hat{m}}_{2}^{1} + {\hat{m}}_{2}^{2} + {\hat{m}}_{2}^{3} - {\hat{x}}_{3} {\hat{f}}_{3}^{3} - {\hat{x}}_{2} {\hat{f}}_{3}^{2} = 0,

{\hat{f}}_{3}^{1} + {\hat{f}}_{3}^{2} + {\hat{f}}_{3}^{3} = 0,

which represent the equations of moment equilibrium about the ${\hat{x}}_{1}$ -axis, moment equilibrium about the ${\hat{x}}_{2}$ -axis, and force equilibrium in the ${\hat{x}}_{3}$ -direction.

Hourglass control

Since the one-point quadrature is used, several spurious modes, often known as hourglass modes, are possible for the quadrilateral elements. To suppress the hourglass modes, a consistent spurious mode control as described by Belytschko et al. (1984) is used. The hourglass shape vector $γ^{I}$ is defined as

γ^{I} = h^{I} - B_{α}^{I} {\hat{x}}_{α}^{J} h^{J} .

The hourglass strain rates are obtained by

{\dot{q}}_{α}^{B} = γ^{I} {\hat{θ}}_{α}^{I},

{\dot{q}}_{3}^{B} = γ^{I} {\hat{v}}_{3}^{I},

{\dot{q}}_{α}^{M} = γ^{I} {\hat{v}}_{α}^{I},

where the superscripts B and M denote hourglass modes associated with bending and in-plane (membrane) response, respectively. The corresponding generalized hourglass stresses for the element S4RS are given by

{\dot{Q}}_{α}^{B} = γ_{r} s^{r} \frac{h^{3} E A}{192} B_{β}^{I} B_{β}^{I} {\dot{q}}_{α}^{B},

{\dot{Q}}_{3}^{B} = γ_{w} s^{w} \frac{κ h^{3} G A}{12} B_{β}^{I} B_{β}^{I} {\dot{q}}_{3}^{B},

{\dot{Q}}_{α}^{M} = γ_{s} s^{s} \frac{h E A}{8} B_{β}^{I} B_{β}^{I} {\dot{q}}_{α}^{M},

where h is the thickness of the shell and E and G are Young's modulus and shear modulus, respectively. The default hourglass control parameters are $γ_{s}$ = $γ_{r}$ =0.050 and $γ_{w}$ =0.005. The scaling factors $s^{r}$ , $s^{r}$ , and $s^{w}$ (by default $s^{r}$ = $s^{r}$ = $s^{w}$ =1) are used to change the corresponding default hourglass control parameters by the user. For the S4RSW element the generalized hourglass stresses ${\dot{Q}}_{3}^{B}$ and ${\dot{Q}}_{α}^{M}$ are the same as those in the element S4RS, but the generalized hourglass stress ${\dot{Q}}_{α}^{B}$ is modified to

{\dot{Q}}_{α}^{B} = γ_{r} s^{r} \frac{h^{3} E A}{192} (1 + \frac{2 κ A}{3 h^{2}}) B_{β}^{I} B_{β}^{I} {\dot{q}}_{α}^{M} .

The nodal hourglass forces and moments corresponding to the generalized hourglass stresses are

{\hat{m}}_{α}^{h I} = γ^{I} Q_{α}^{B},

{\hat{f}}_{3}^{h I} = γ^{I} Q_{3}^{B},

{\hat{f}}_{α}^{h I} = γ^{I} Q_{α}^{M} .

These hourglass forces and moments are added directly to the local nodal forces and moments described previously.