Rebar modeling in two dimensions | ||||||
|
| |||||
ProductsAbaqus/StandardAbaqus/Explicit
Let be the element's usual isoparametric coordinates. Let r be an isoparametric coordinate along the line where the face of the element intersects the plane of reinforcement, with in an element (see Figure 1).
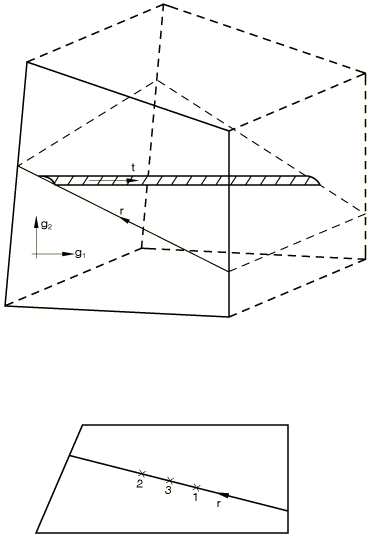
The plane of reinforcement is always perpendicular to the element face.
The rebar will be integrated at one or two points, depending on the order of interpolation in underlying elements. The volume of integration , position, rebar strain , and first and second variations of rebar strain and at each point are calculated as
where
is the original thickness for plane elements and for axisymmetric elements;
is the rebar cross-sectional area;
is the spacing of rebar (for axisymmetric elements , where is the radius where the spacing is given);
is the Gauss weight associated with the integration point along the line;
is position; and
Strain is
where and measure length along the rebar in the current and initial configurations, respectively.
For the deformations allowed in these elements,
where is the orientation of the rebar from the plane of the model,
is the squared stretch ratio in the r-direction, and is the stretch ratio in the thickness direction:
for plane stress or plane strain;
for generalized plane strain, where t is given in Generalized plane strain elements; and
for axisymmetric elements.
From these results the first variation of strain is
where
for plane stress and plane strain,
for generalized plane strain, and
for axisymmetric cases.
The second variation of strain is then