Continuity statement for the wetting liquid phase in a porous medium | |||||||
|
| ||||||
ProductsAbaqus/Standard
The wetting liquid can attach to and, thus, be trapped by certain solid particles in the medium: this volume of trapped liquid attached to solid particles forms a “gel.”
A porous medium is modeled approximately in Abaqus by attaching the finite element mesh to the solid phase. Liquid can flow through this mesh. A continuity equation is, therefore, required for the liquid, equating the rate of increase in liquid mass stored at a point to the rate of mass of liquid flowing into the point within the time increment. This continuity statement is written in a variational form as a basis for finite element approximation. The liquid flow is described by introducing Darcy's law or, alternatively, Forchheimer's law. The continuity equation is satisfied approximately in the finite element model by using excess wetting liquid pressure as the nodal variable (degree of freedom 8), interpolated over the elements. The equation is integrated in time by using the backward Euler approximation. The total derivative of this integrated variational statement of continuity with respect to the nodal variables is required for the Newton iterations used to solve the nonlinear, coupled, equilibrium and continuity equations. This expression is also derived in this section.
Consider a volume containing a fixed amount of solid matter. In the current configuration this volume occupies space V with surface S. In the reference configuration it occupied space . Wetting liquid can flow through this volume: at any time the volume of such “free” liquid (liquid that can flow if driven by pressure) is written . Wetting liquid can also become trapped in the volume, by absorption into the gel. The volume of such trapped liquid is written .
The total mass of wetting liquid in the control volume is
where is the mass density of the liquid.
The time rate of change of this mass of wetting liquid is
The mass of wetting liquid crossing the surface and entering the volume per unit time is
where is the average velocity of the wetting liquid relative to the solid phase (the seepage velocity) and is the outward normal to S.
Equating the addition of liquid mass across the surface S to the rate of change of liquid mass within the volume V gives the wetting liquid mass continuity equation
Using the divergence theorem and because the volume is arbitrary, this provides the pointwise equation
The equivalent weak form is
where is an arbitrary, continuous, variational field. This statement can also be written on the reference volume:
In Abaqus/Standard this continuity statement is integrated approximately in time by the backward Euler formula, giving
which, over the current volume, is
We now drop the subscript by adopting the convention that any quantity not explicitly associated with a point in time is taken at .
The divergence theorem allows the equation to be rewritten as
where—for convenience—we have normalized the equation by the density of the liquid in the reference configuration, .
Since , this is the same as
Constitutive behavior
The constitutive behavior for pore fluid flow is governed either by Darcy's law or by Forchheimer's law. Darcy's law is generally applicable to low fluid flow velocities, whereas Forchheimer's law is commonly used for situations involving higher flow velocities. Darcy's law can be thought of as a linearized version of Forchheimer's law. Darcy's law states that, under uniform conditions, the volumetric flow rate of the wetting liquid through a unit area of the medium, , is proportional to the negative of the gradient of the piezometric head (Bear, 1972):
where is the permeability of the medium and is the piezometric head, defined as
where z is the elevation above some datum and g is the magnitude of the gravitational acceleration, which acts in the direction opposite to z. On the other hand, Forchheimer's law states that the negative of the gradient of the piezometric head is related to a quadratic function of the volumetric flow rate of the wetting liquid through a unit area of the medium (Desai, 1975):
where is a “velocity coefficient” (Tariq, 1987). This nonlinear permeability can be defined to be dependent on the void ratio of the material. We see that, as the fluid velocity tends to zero, Forchheimer's law approaches Darcy's law. Also, if , the two flow laws are identical.
can be anisotropic and is a function of the saturation and void ratio of the material. has units of velocity (length/time). [Some authors refer to as the hydraulic conductivity (Bear, 1972) and define the permeability as
where is the kinematic viscosity of the fluid (the ratio of the fluid's dynamic viscosity to its density).]
We assume that g is constant in magnitude and direction, so
where is the gravitational acceleration (we assume that varies slowly with position).
The permeability of a particular fluid in a multiphase flow system depends on the saturation of the phase being considered and on the porosity of the medium. We assume these dependencies are separable, so
where provides the dependency on saturation, with and is the permeability of the fully saturated medium.
The function can be defined by the user. Nguyen and Durso (1983) observe that, in steady flow through a partially saturated medium, the permeability varies with . We, therefore, take by default.
Introducing the flow constitutive law allows the mass continuity equation (Equation 1) to be written
![]()
Volumetric strain in the liquid and grains
The bulk behavior of the grains was discussed in Constitutive behavior in a porous medium. From Equation 2,
Combining this with Equation 4 and neglecting all but first-order terms in small quantities, we obtain
Using Equation 1 and again neglecting second-order terms in small quantities, we obtain
Combining this result with Equation 4 and again approximating to first-order in small quantities,
![]()
Saturation
Because measures pressure in the wetting liquid and we neglect the pressure in the other fluid phase in the medium (see Effective stress principle for porous media), the medium is fully saturated for . Negative values of represent capillary effects in the medium. For it is known (see, for example, Nguyen and Durso, 1983) that, at a given value of capillary pressure, , the saturation lies within certain limits. Typical forms of these limits are shown in Figure 1.
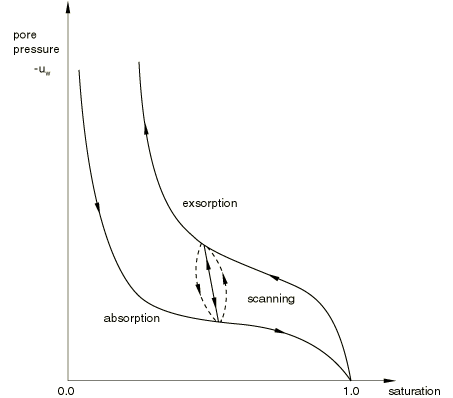
We write these limits as , where is the limit at which absorption will occur (so that ), and is the limit at which exsorption will occur, and thus . We assume that these relationships are uniquely invertible and can, thus, also be written as during absorption and during exsorption. We also assume that some wetting liquid will always be present in the medium: .
Bear (1972) suggests that the transition between absorption and exsorption and vice versa takes place along “scanning” curves. We approximate these with a straight line, as shown in Figure 1.
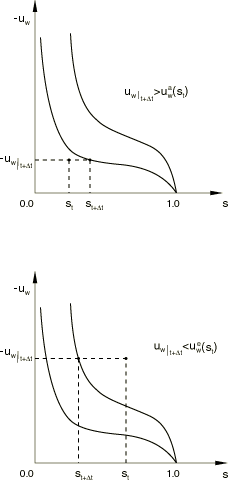
Saturation is treated as a state variable that may have to change if the wetting liquid pressure is outside the range for which its value is admissible according to that actual data corresponding to Figure 1. The evolution of saturation as a state variable is defined as follows. Assume that the saturation at time t, , is known. It must satisfy the constraints
We solve the continuity equation for , initially assuming . We then obtain by the following rules:
where is the slope of the scanning line. These choices are shown in Figure 2.
![]()
Jacobian contribution
The Jacobian contribution from the continuity equation is obtained from the variation of Equation 2 with respect to and at time .
Consider first the surface integral. The surface divides into that part across which the liquid mass flow rate, , is prescribed and that part where the wetting liquid pressure, , is prescribed. Thus, the only contribution of this term to the Jacobian is the variation in the integral caused by change in surface area in that part where the mass flow is prescribed. We neglect this contribution.
The remaining part of the variation of Equation 2 is
Using Equation 3 we have
and, thus, neglecting small terms compared to unity,
Equation 5 shows that , which is defined by the evolution equation given in Constitutive behavior in a porous medium and so makes no contribution to the Jacobian.
Finally, the Jacobian contribution from the permeability term is rather complex in the general case of the nonlinear Forchheimer flow law. Although we include it in the software, here we only write the linearized flow version reflecting Darcy's law ():
Using these results provides the Jacobian of the continuity equation as