Constitutive model for jointed materials | ||||||
|
| |||||
ProductsAbaqus/Standard
The model implemented in Abaqus/Standard provides for opening of the joints, or frictional sliding of the joints, in each of these systems (a “system” in this context is a joint orientation in a particular direction at a material calculation point). In addition to the joint systems, the model includes a bulk material failure mechanism. This is based on the Drucker-Prager failure criterion.
Joint system definitions
We consider a particular joint a oriented by the normal to the joint surface . We define as two unit, orthogonal vectors in the joint surface. The local stress components are the pressure stress across the joint
and the shear stresses across the joint
where is the stress tensor. We define the shear stress magnitude as
The local strain components are the normal strain across the joint
and the engineering shear strain in the -direction in the joint surface
where is the strain tensor.
![]()
Strain rate decomposition
A linear strain rate decomposition is assumed, so that
where is the total strain rate, is the elastic strain rate, and is the inelastic (plastic) strain rate. Supposing that several systems are active (we designate an active system by i, where indicates the bulk material system and is a joint system a), we write
![]()
Elasticity and joint opening/closing
When all joints at a point are closed, the elastic behavior of the material is assumed to be isotropic and linear. The material cannot be elastically incompressible (Poisson's ratio must be less than 0.5).
We use a stress-based joint opening criterion whereas joint closing is monitored based on strain. Joint system a opens when the estimated pressure stress across the joint (normal to the joint surface) is no longer positive:
In this case the material is assumed to have no elastic stiffness with respect to direct strain across the joint system. Open joints, thus, create anisotropic elastic response at a point. The joint system remains open as long as
where is the component of direct elastic strain across the joint and is the component of direct elastic strain across the joint calculated in plane stress as
where E is the Young's modulus of the material, is the Poisson's ratio, and
are the direct stresses in the plane of the joint.
The shear response of open joints is governed by the shear retention parameter, , which represents the fraction of the elastic shear modulus retained when the joints are open (=0 means no shear stiffness associated with open joints, while =1 corresponds to elastic shear stiffness in open joints; any value between these two extremes can be used).
![]()
Plastic behavior of joint systems
The failure surface for sliding on joint system a is defined by
where is the friction angle for system a, and is the cohesion for system a (see Figure 1).
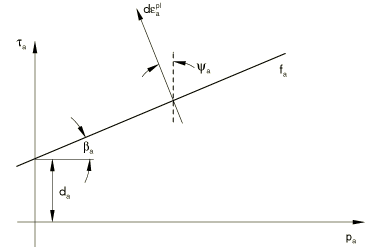
As long as , joint system a does not slip. When joint system a slips. The inelastic (“plastic”) strain on the system is then given by
where is the rate of inelastic shear strain in direction on the joint surface, is the magnitude of the inelastic strain rate, is the dilation angle for this joint system (choosing provides pure shear flow on the joint, while causes dilation of the joint as it slips), and is the inelastic strain normal to the joint surface. In order to add the plastic flow contributions from different systems we write the tensorial plastic strain rate for joint a as
The sliding of the different joint systems at a point is independent, in the sense that sliding on one system does not change the failure criterion or the dilation angle for any other joint system at the same point. The model provides for up to three joint systems at a point.
![]()
Plastic behavior of bulk material
In addition to the joint systems, the model includes a bulk material failure mechanism. This is based on the Drucker-Prager failure criterion,
where is the Mises equivalent deviatoric stress (here is the deviatoric stress ), is the equivalent pressure stress, is the friction angle for the bulk material, and is the cohesion for the bulk material (see Figure 2).
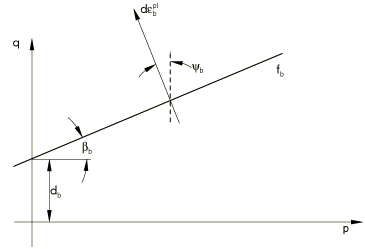
If this failure criterion is reached, the bulk inelastic flow is defined by
where
is the flow potential. Here, is the magnitude of the inelastic flow rate (chosen so that in uniaxial compression in the 1-direction) and is the dilation angle for the bulk material. This bulk failure model is a simplified version of the extended Drucker-Prager model described in Models for granular or polymer behavior. As with the joint systems, this bulk failure system is independent of the joint systems, in that bulk inelastic flow does not change the behavior of any joint system.
If in any system the flow in that system is “nonassociated.” This implies that the material stiffness matrix is not symmetric, so that the unsymmetric matrix solution scheme should be invoked by the user. If the difference between and is not large, a symmetric approximation to the matrix can provide an acceptable rate of convergence of the equilibrium equations, and hence a lower overall solution cost. For this reason the unsymmetric solver is not automatically invoked for this material behavior. However, it is recommended for all cases where and are very different on any joint system.
![]()
Integration of the model
The constitutive equations described above are integrated using the backward Euler method generally used with the plasticity models in Abaqus. A material Jacobian consistent with this integration operator is used for the overall equilibrium iterations.