Hydrostatic fluid calculations

In Abaqus/Standard the fluid is incompressible by default and the fluid volume, $\overline{V}$, is dependent upon temperature but independent of the fluid pressure:

If compressibility is introduced, the fluid volume depends upon both the temperature and pressure:

where K is the fluid bulk modulus and ${\rho }_R$ is the reference fluid density at zero pressure and the initial temperature.

The total fluid mass in the cavity is the sum of the fluid masses of the elements making up the cavity:

The mass of a fluid element in the cavity, $m^e$, is calculated from the initial fluid density, $\rho \left(p_I,{\theta }_I\right)$, and the initial element volume, $V_I^e$:

where $p_I$ is the initial fluid pressure and ${\theta }_I$ is the initial temperature. The initial fluid density follows from the user-defined reference density, ${\rho }_R$:

The fluid density at the current pressure and temperature, $\rho \left(p,\theta \right)$, is obtained as

where ${\theta }_0$ is the reference temperature for the coefficient of thermal expansion and $\alpha \left(\theta \right)$ is the mean (secant) coefficient of thermal expansion, and it is assumed that $\left|\rho /{\rho }_R-1\right|\ll 1$.

Thus, the fluid volume at the current pressure and temperature is

This volume can be calculated on an element by element basis:

Fluid can be added to or removed from the cavity. The amount of fluid added is given as the change in (fluid) mass $\mathrm{\Delta }m$. Consequently, the change of the fluid volume at the current cavity temperature is

In this case the fluid is compressible, and the volume is a function of the pressure and the temperature in the cavity:

where, as before, the total fluid mass in the cavity is the sum of the masses of the elements in the cavity. The fluid is assumed to behave like an ideal gas; hence, the density of the fluid in the cavity can be calculated as

where $R$ is the gas constant, ${\theta }_A$ is the temperature at absolute zero, and $p_A$ is the ambient pressure. The current fluid volume can again be calculated on an element by element basis:

The corresponding volume-pressure compliance is

Fluid can be added to or removed from the cavity. The amount of fluid added is again given as the change in (fluid) mass. Consequently, the change of the fluid volume at the current cavity temperature is

The hydrostatic fluid elements appear as surface elements that cover the cavity boundary, but they are actually volume elements when the cavity reference node is accounted for. Figure 1 depicts the 4-node hydrostatic fluid volume element, F3D4. The dashed lines indicate that the element is actually pyramidal in shape.

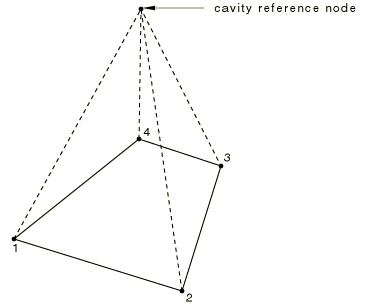
The volume, $V^e$, of each element must be calculated. The coordinates of any point on the base of the pyramid element can be found by

where $N^N$ are the interpolation functions for the base of the pyramid (Solid isoparametric quadrilaterals and hexahedra), expressed in terms of parametric coordinates g and h; ${\mathbf{x}}^N$ are the nodal coordinates; and the summation extends over all nodes on the base. For three-dimensional elements the Jacobian on the surface is calculated as

The normal to the element face, $\mathbf{n}$, multiplied by an infinitesimal area, $dA$, of the element face is, hence, obtained as

The infinitesimal volume, $dV$, associated with this infinitesimal area is

where ${\mathbf{x}}_R$ is the position of the cavity reference node. The volume of the element, $V^e$, is then obtained by integration. For a quadrilateral base this yields

The integration boundaries will be different for a triangular base. Introducing the relative position, $\overline{\mathbf{x}}=\mathbf{x}-{\mathbf{x}}_R$, this becomes

The variation in the element volume is readily obtained as

This expression includes contributions to the volume change due to variation in the “sides” of the pyramid element. Hence, the equivalent forces will also include the effect of the pressure on these sides. The pressure on the sides will be balanced by the pressure on the side of the adjacent pyramid element; hence, we only need to calculate the contribution from the pressure on the “base” of the pyramid. This can be done by separating the contributions by using partial integration, which yields

The last two integrals represent the contributions on the sides of the pyramid; hence, the resulting expression is

This equation can readily be obtained directly (see Pressure load stiffness).

The second variation of the expression for the volume is

Similar expressions can be obtained for planar and axisymmetric fluid elements. For a planar element the volume is readily obtained as

where ${\mathbf{e}}_3$ is the unit vector in the direction perpendicular to the plane. Similarly, for axisymmetric elements

The first and second variations are obtained in the same way as for three-dimensional elements.

The integrations can be carried out analytically. For example, for element type F3D4 the above expressions yield, after some manipulation,

where ${\overline{\mathbf{x}}}^N$, $N=1,4$ denote the relative nodal coordinates. The first variation (involving the base only) is equal to

and the second variation of the volume is

Abaqus provides a capability that can be used to model fluid flow between two cavities or between a cavity and the outside world. This is typically used when the fluid has to flow through a narrow orifice. It is assumed that the mass flow rate, q, is a homogeneous function of the pressure difference, $\mathrm{\Delta }p=p_1-p_2$. In addition, it is assumed that the flow rate may depend on the average temperature—$\overline{\theta }=\left({\theta }_1+{\theta }_2\right)/2$—and, for a compressible fluid, on the average pressure—$\overline{p}=\left(p_1+p_2\right)/2$:

The flow rate needs to be integrated over a finite increment. We assume that the dependence on the average pressure, $\overline{p}$, is weak. Hence, we use a semi-implicit method: we use $\mathrm{\Delta }p$ at the end of the increment and ${\overline{p}}^0$ at the start of the increment. For the temperature we choose ${\overline{\theta }}^m$ to be the average of $\overline{\theta }$ at the start and end of the increment, because this is likely to be the most accurate. Hence, we obtain the mass flow as:

This mass change needs to be converted to a volume change in each cavity. It is assumed that the fluid in both cavities is the same, but the pressures (and possibly the temperatures) may be different. With use of the pressure and temperature-dependent density ${\rho }_i\left(p,\theta \right)$ for each cavity i, the relations become

and

Observe that, except for isothermal incompressible fluids, the resulting matrix is nonsymmetric. For an incompressible fluid with thermal expansion, the nonsymmetric contribution is small and the equations can be symmetrized without significant degradation in convergence rate. For an ideal gas, the nonsymmetric terms can have a significant effect if the drop in pressure is large.

Many applications of fluid flow between cavities involve dynamic loading in the form of steady-state vibration; and often in such cases the dissipative losses in the link between the cavities must be modeled to obtain useful results. In most problems of this class the fluids on either side of the fluid link are first pressurized statically. In the implementation in Abaqus/Standard, it is assumed that the vibration amplitude is sufficiently small that the fluid link response in the dynamic phase of the problem can be treated as linear perturbations about the prepressurized state.

For small vibrations about a prepressurized state we linearize Equation 1 to give

The mass flow through the link can, therefore, be derived as follows:

Substituting the above expression for mass flow into Equation 2 and noting that ${\mathrm{\Delta }m|}_0=0$ yields

In Abaqus this model is provided only for the direct-solution steady-state dynamic analysis procedure.

It is possible that negative eigenvalues will be encountered in the solution of certain hydrostatic fluid element problems. With standard elements this can indicate that a bifurcation or buckling load has been exceeded. However, this is not necessarily true with hydrostatic fluid elements; negative eigenvalues can result solely from the numerical implementation.

Consider the simple hydrostatic fluid model depicted in Figure 2.

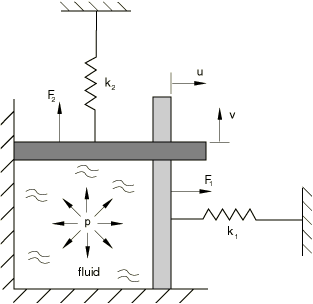
If the fluid is considered incompressible, application of the downward force causes the fluid to compress vertically and expand horizontally, while maintaining the original fluid volume. Thus, the model can be adequately discretized as a three degree of freedom system: the horizontal displacement of the right platen, u; the vertical displacement of the top platen, v; and the fluid pressure, p. The corresponding system of equations in matrix form is

The equation solver processes the equations in sequence. Hence, it will process the $2\times 2$ submatrix relating the displacements to the forces prior to processing the constraints. This leads to a negative eigenvalue if $p^2>k_1{k}_2$. However since the mode associated with the negative eigenvalue is subsequently constrained by the continuity equation, no instability occurs.