Models for crushable foams

Abaqus uses two phenomenological constitutive models for the analysis of crushable foams typically used in energy absorption structures. Both the volumetric hardening model and the isotropic hardening model use a yield surface with an elliptical dependence of deviatoric stress on pressure stress in the meridional plane.

The following topics are discussed:

The strain rate decomposition
Elastic behavior
Plastic behavior
Crushable foam model with volumetric hardening
Crushable foam model with isotropic hardening

The strain rate decomposition

The volume change is decomposed as

\begin{matrix} (1) & J = J^{e l} \cdot J^{p l}, \end{matrix}

where J is the ratio of current volume to original volume, $J^{e l}$ is the elastic (recoverable) part of the ratio of current to original foam volume, and $J^{p l}$ is the plastic (nonrecoverable) part of the ratio of current to original foam volume.

Volumetric strains are defined as

\begin{matrix} ε_{vol} & = \ln J, \\ ε_{vol}^{e l} & = \ln J^{e l}, \\ ε_{vol}^{p l} & = \ln J^{p l} . \end{matrix}

These definitions and Equation 1 result in the usual additive strain rate decomposition for volumetric strains:

{\dot{ε}}_{vol} = {\dot{ε}}_{vol}^{e l} + {\dot{ε}}_{vol}^{p l} .

The model also assumes the deviatoric strain rates decompose additively, so that the total strain rates decompose as

\dot{ε} = {\dot{ε}}^{e l} + {\dot{ε}}^{p l} .

Elastic behavior

The elastic behavior can be modeled only as linear elastic

σ = D^{e l} : ε^{e l},

where $D^{e l}$ represents the fourth-order elasticity tensor and $σ$ and $ε^{e l}$ are the second-order stress and elastic strain tensors, respectively.

Plastic behavior

The yield surface and the flow potential for the crushable foam models are defined in terms of the pressure stress

p = - \frac{1}{3} trace σ = - \frac{1}{3} σ : I

and the Mises stress

q = \sqrt{\frac{3}{2} S : S} .

The yield surface is defined as

\begin{matrix} (2) & F = \sqrt{q^{2} + α^{2} {(p - p_{0})}^{2}} - B = 0 \end{matrix}

and the flow potential is defined as

\begin{matrix} (3) & G = \sqrt{q^{2} + β^{2} p^{2}} . \end{matrix}

F and G can each be represented as an ellipse in the p–q stress plane with $α$ and $β$ representing the shape of the yield ellipse and the ellipse for the flow potential, respectively; $p_{0}$ is the center of the yield ellipse, and B is the length of the (vertical) q–axis of the yield ellipse. The flow potential is an ellipse centered in the origin. The yield surface and the flow potential are depicted in Figure 1.

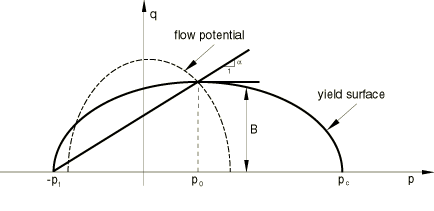
Figure 1. Typical yield surface and flow potential for the crushable foam model.

The parameters $p_{0}$ and B of the yield ellipse (Equation 2) are related to the yield strength in hydrostatic compression, $p_{c}$ , and to the yield strength in hydrostatic tension, $p_{t}$ , by

p_{0} = \frac{p_{c} - p_{t}}{2} and B = α A = α \frac{p_{c} + p_{t}}{2},

where $p_{c}$ and $p_{t}$ are positive quantities and A is the length of the (horizontal) p-axis of the yield ellipse.

The shape factor, $α$ , remains as a constant during any plastic deformation process. The evolution of the yield ellipse is controlled by a plastic strain measure, $\bar{ε}$ , which is the volumetric compacting plastic strain, $- ε_{vol}^{p l}$ , for the volumetric hardening model, and the equivalent plastic strain, ${\bar{ε}}^{p l}$ (to be defined later), for the isotropic hardening model.

To define the hardening behavior, uniaxial compression test data are required. A piecewise linear hardening curve of uniaxial Cauchy stress versus axial (logarithmic) plastic strain must be entered in a tabular form.

Crushable foam model with volumetric hardening

The volumetric hardening model assumes that the hydrostatic tension strength, $p_{t}$ , remains constant throughout any plastic deformation process. By contrast, the hydrostatic compression strength evolves as a result of compaction (increase in density) or dilation (reduction in density) of the material:

p_{c} = p_{c} (\bar{ε}) where \bar{ε} \equiv - ε_{vol}^{p l} = - trace ε^{p l} .

Yield surface

The yield surface for the crushable foam model, depicted in Figure 2,

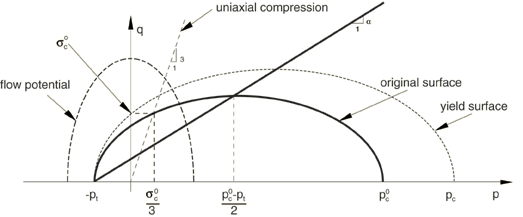
Figure 2. Yield surfaces and flow potential for the volumetric hardening model.

is defined by

F = \sqrt{q^{2} + α^{2} {(p - p_{0})}^{2}} - B = 0,

where the parameter $α$ represents the shape of the yield ellipse in the p–q stress plane and can be calculated from the initial yield strength in uniaxial compression, $σ_{c}^{0}$ , taken as a positive value; the initial yield strength in hydrostatic compression, $p_{c}^{0}$ ; and the yield strength in hydrostatic tension, $p_{t}$ ; as

α = \frac{3 k}{\sqrt{(3 k_{t} + k) (3 - k)}} with k = \frac{σ_{c}^{0}}{p_{c}^{0}} and k_{t} = \frac{p_{t}}{p_{c}^{0}},

where the yield stress ratios, $k (θ, f_{i})$ and $k_{t} (θ, f_{i})$ , are provided by the user and can be functions of temperature and other field variables. For a valid yield surface the choice of yield stress ratios must be such that $0 < k < 3$ and $k_{t} \geq 0$ . The yield surface is the Mises circle in the deviatoric stress plane.

Flow potential

The plastic strain rate for the volumetric hardening model is assumed to be

{\dot{ε}}^{p l} = {\dot{\bar{ε}}}^{p l} \frac{\partial G}{\partial σ},

where ${\dot{\bar{ε}}}^{p l}$ is the equivalent plastic strain rate defined as

{\dot{\bar{ε}}}^{p l} = \frac{σ : {\dot{ε}}^{p l}}{G},

and G is the flow potential, chosen in this model as

\begin{matrix} (4) & G = \sqrt{q^{2} + \frac{9}{2} p^{2}} . \end{matrix}

This potential is a particular case of Equation 3 with $β = 3 / \sqrt{2} \approx 2.12$ . A geometrical representation of the flow potential in the p–q stress plane is shown in Figure 2.

Equation 4 gives a direction of flow that is identical to the stress direction for radial paths. This is motivated by simple laboratory experiments performed by Bilkhu (1987), which suggest that loading in any principal direction causes insignificant deformation in the other directions. As a result, the plastic flow is nonassociative. Therefore, the use of this foam model generally requires the solution of nonsymmetric equations.

Hardening

The yield surface intersects the p-axis at $- p_{t}$ and $p_{c}$ . We assume that $p_{t}$ remains fixed throughout any plastic deformation process. By contrast, the compressive strength, $p_{c}$ , evolves as a result of compaction (increase in density) or dilation (reduction in density) of the material. The evolution of the yield surface can be expressed through the evolution of the yield surface size on the hydrostatic stress axis, $p_{c} + p_{t}$ , as a function of the value of volumetric compacting plastic strain, $- ε_{vol}^{p l}$ . With $p_{t}$ constant, this relation can be obtained from a user-provided uniaxial compression test data using

p_{c} (ε_{vol}^{p l}) = \frac{σ_{c} (ε_{axial}^{p l}) [σ_{c} (ε_{axial}^{p t}) (\frac{1}{α^{2}} + \frac{1}{9}) + \frac{p_{t}}{3}]}{p_{t} + \frac{σ_{c} (ε_{axial}^{p l})}{3}}

along with the fact that $ε_{axial}^{p l} = ε_{vol}^{p l}$ in uniaxial compression (due to zero plastic Poisson's ratio). Thus, the user provides input to the hardening law by only specifying, in the usual tabular form, the value of the yield stress in uniaxial compression as a function of the absolute value of the axial plastic strain. The table must start with a zero plastic strain (corresponding to the virgin state of the material), and the tabular entries must be given in ascending magnitude of $ε_{axial}^{p l}$ . If desired, the yield stress can also be a function of temperature and other predefined field variables.

Crushable foam model with isotropic hardening

The isotropic hardening model was originally developed for metallic foams by Deshpande and Fleck (2000). The model assumes similar behaviors in tension and compression. The yield surface is an ellipse centered at the origin in the p–q stress plane and evolves in a self-similar manner governed by the equivalent plastic strain.

Yield surface

The yield surface for the isotropic hardening model is defined as

\begin{matrix} (5) & F = \sqrt{q^{2} + α^{2} p^{2}} - B = 0 \end{matrix}

with

B = α p_{c} = σ_{c} \sqrt{1 + {(\frac{α}{3})}^{2}},

where $α$ represents the shape of the yield ellipse in the p–q stress plane, B defines the size of the yield ellipse, $p_{c}$ is the yield strength in hydrostatic compression, and $σ_{c}$ is the absolute value of the yield strength in uniaxial compression. The yield surface is the Mises circle in the deviatoric stress plane, and an ellipse in the meridional plane as depicted in Figure 3.

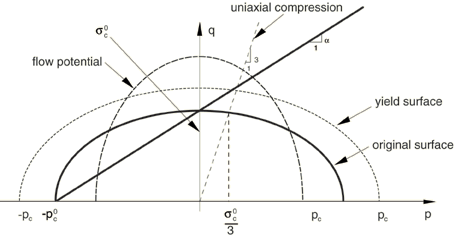
Figure 3. Yield surfaces and flow potential for the isotropic hardening model.

The parameter $α$ can be calculated using the initial yield stress in uniaxial compression, $σ_{c}^{0}$ , and the initial yield stress in hydrostatic compression, $p_{c}^{0}$ , as

α = \frac{3 k}{\sqrt{9 - k^{2}}} with k = \frac{σ_{c}^{0}}{p_{c}^{0}} .

The strength ratio k is provided by the user and must be in the range of 0 and 3. For many low-density foams the initial yield surface is close to a circle in the p–q stress plane, which indicates that the value of $α$ is approximately one. The special case of $k = 0$ corresponds to the Mises yield surface.

Flow potential

The flow potential for the isotropic hardening model is chosen as

G = \sqrt{q^{2} + β^{2} p^{2}},

where $β$ represents the shape of the flow potential in the p–q stress plane and is related to the plastic Poisson's ratio, $ν_{p}$ , by

β = \frac{3}{\sqrt{2}} \sqrt{\frac{1 - 2 ν_{p}}{1 + ν_{p}}} .

The plastic Poisson's ratio, which is the ratio of the transverse to the longitudinal plastic strain under uniaxial compression, should be defined by the user; and it must be in the range of −1 and 0.5. The upper limit, $ν_{p} = 0.5$ , corresponds to an incompressible plastic flow.

The plastic strains are defined to be normal to a family of self-similar flow potentials parametrized by the value of the potential G

{\dot{ε}}^{p l} = \dot{λ} \frac{\partial G}{\partial σ},

where $\dot{λ}$ is the nonnegative plastic flow multiplier. The hardening of the foam is described through $σ_{c} = σ_{c} ({\bar{ε}}^{p l})$ , where ${\bar{ε}}^{p l}$ is the equivalent plastic strain. The evolution of ${\bar{ε}}^{p l}$ is assumed to be governed by the equivalent plastic work expression; i.e.,

σ_{c} {\dot{\bar{ε}}}^{p l} = σ : {\dot{ε}}^{p l} .

The equivalent plastic strain is equal to the absolute value of the axial plastic strain in uniaxial tension or compression.

The plastic flow is associative when the value of $β$ is the same as that of $α$ . In general, the plastic flow is nonassociated to allow for the independent calibrations of the shape of the yield surface and the plastic Poisson's ratio. For many low-density foams the plastic Poisson's ratio is nearly zero, which corresponds to a value of $β \approx 2.12$ .

Hardening

A simple uniaxial compression test is sufficient to define the evolution of the yield surface. The hardening law defines the value of the yield stress in uniaxial compression as a function of the absolute value of the axial plastic strain. The piecewise linear relationship is entered in tabular form. The table must start with a zero plastic strain (corresponding to the virgin state of the materials) and must be given in ascending magnitude of $ε_{axial}^{p l}$ . If desired, the yield stress can also be a function of temperature and other predefined field variables.