Probability density function

A probability density function (PDF) describes the probability of the value of a continuous random variable falling within a range. If the random variable can only have specific values (like throwing dice), a probability mass function (PMF) would be used to describe the probabilities of the outcomes. The plot on the left in Figure 1 shows a PDF for the random variable $x$ . The probability that the random variable has a value in the range $x$ and $x + d x$ is $f (x) d x$ . The probability that the random variable $x$ will be in the range $a \leq x \leq b$ is given by:

\Pr [a \leq x \leq b] = \int_{a}^{b} f (x) d x .

The probability that the random variable $x$ is in the range $- \infty$ and $\infty$ is one; i.e.,

\int_{- \infty}^{\infty} f (x) d x = 1.

The area under the PDF curve is, therefore, always unity.

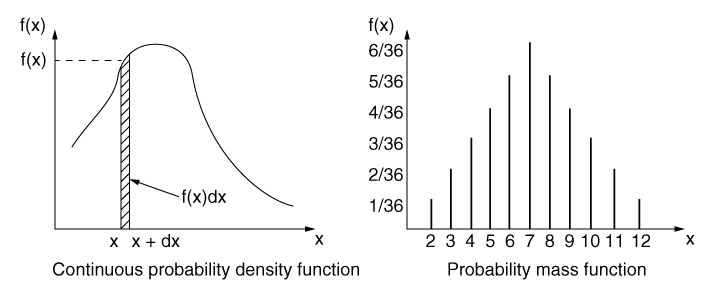
Figure 1. Probability distributions of continuous and discrete variables.

The plot on the right in Figure 1 shows a PMF where the horizontal axis shows the specific values of the random variable and the vertical axis shows the corresponding probabilities.

Abaqus/Explicit supports uniform, normal (Gaussian), log-normal, piecewise linear, and discrete probability density functions. To define a probability density function, you must assign it a name and specify its type.

Input File Usage

PROBABILITY DENSITY FUNCTION, NAME=PDF_name,
TYPE=PDF_type

Uniform probability density function

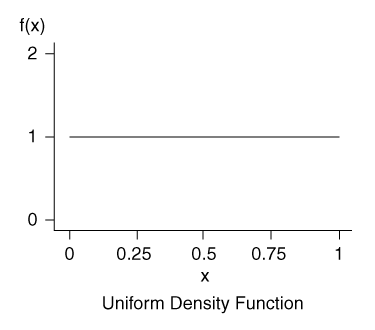
Uniform distributions (shown in Figure 2) have many applications, particularly in the numerical simulation of random processes. The following function describes a uniform probability density function for a random variable $x$ between $x_{min}$ and $x_{max}$ :

f (x) = {\begin{matrix} \frac{1}{x_{max} - x_{min}} & x_{min} \leq x \leq x_{max} \\ 0 & otherwise \end{matrix} .

The mean is $μ = \frac{x_{min} + x_{max}}{2},$ and the variance is $σ^{2} = \frac{{(x_{max} - x_{min})}^{2}}{12}$ . You specify $x_{min}$ and $x_{max}$ for the uniform distribution.

Figure 2. Uniform PDF.

Input File Usage

PROBABILITY DENSITY FUNCTION, TYPE=UNIFORM

Normal probability density function

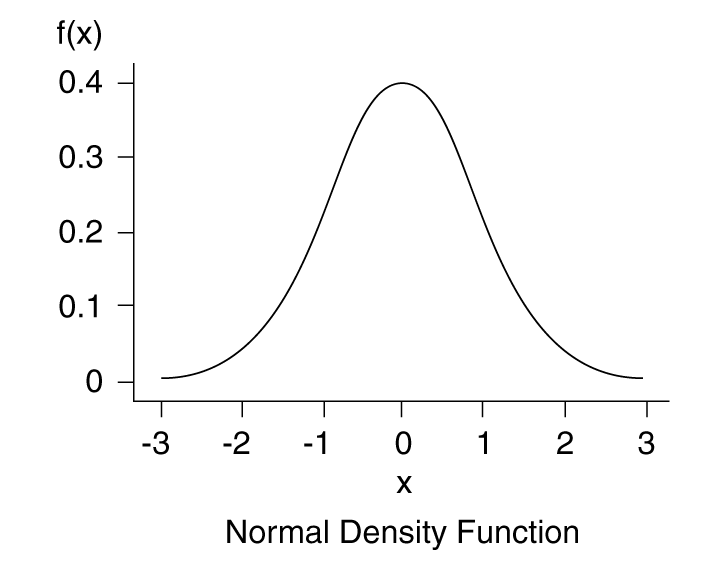
Normal distributions (shown in Figure 3) have many applications in science and engineering; for example, errors in experimental measurements are often assumed to have a normal distribution. The following function describes a normal probability density function:

f (x) = \frac{1}{\sqrt{2 π} σ} e^{[\frac{- {(x - μ)}^{2}}{2 σ^{2}}]} .

The mean is $μ = \frac{1}{N} \sum_{i = 1}^{N} x_{i}$ , and the variance is $σ^{2} = \frac{1}{N} \sum_{i = 1}^{N} {(x_{i} - μ)}^{2}$ . You specify the mean, $μ$ , and standard deviation, $σ$ , for the normal distribution.

Figure 3. Normal PDF.

Input File Usage

PROBABILITY DENSITY FUNCTION, TYPE=NORMAL

Log-normal probability density function

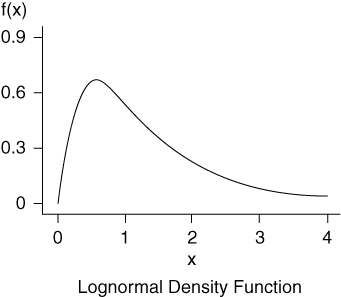
Log-normal distributions (shown in Figure 4) are used in describing many natural phenomena. They are commonly used to describe particle size distributions in soils. The following function describes a log-normal probability density function:

f (x) = {\begin{matrix} \frac{1}{\sqrt{2 π} σ x} e^{[\frac{- {[\ln (x) - μ]}^{2}}{2 σ^{2}}]} & x > 0 \\ 0 & otherwise \end{matrix} .

The mean, $\hat{μ}$ , and standard deviation, $\hat{σ}$ , in the $x$ space are related to $μ$ and $σ$ as follows:

\begin{matrix} \hat{μ} = e^{[μ + \frac{1}{2} σ^{2}]} \\ \hat{σ^{2}} = e^{2 μ} e^{σ^{2}} (e^{σ^{2}} - 1), \end{matrix}

where the parameters $μ$ and $σ$ are the mean and standard deviation in the $\ln (x)$ space; given by $μ = \frac{1}{N} \sum_{i = 1}^{N} \ln (x_{i})$ and $σ = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {(\ln (x_{i}) - μ)}^{2}},$ respectively. You specify the mean, $\hat{μ}$ , and the standard deviation, $\hat{σ}$ , in the $x$ space for the log-normal distribution.

Figure 4. Log-normal PDF.

Input File Usage

PROBABILITY DENSITY FUNCTION, TYPE=LOGNORMAL

Piecewise linear probability density function

A piecewise linear probability density function can be used to approximate general distributions that are not well represented by the other PDF forms discussed above. With a piecewise linear probability density function, you specify PDF values at discrete points. Abaqus/Explicit considers linear variations in the PDF between these points, as shown in Figure 5. The PDF is zero below the first data point and above the last data point.

Figure 5. Piecewise linear PDF.

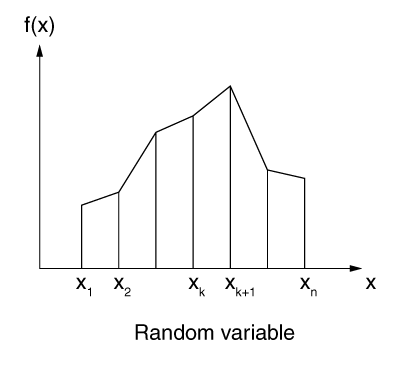
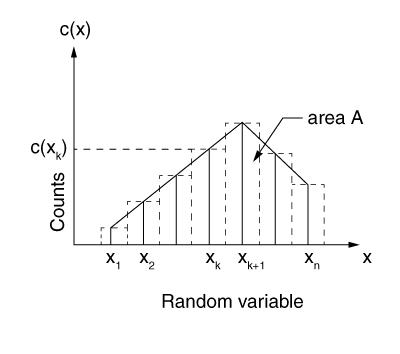
As mentioned earlier, the area under a PDF is unity. Abaqus/Explicit will renormalize the specified PDF data to achieve this requirement. This renormalization of data values allows you to specify relative PDF values that may be obtained from a histogram. A histogram contains the data in the form of a table of random variable ranges and the percentage or number that fall within those ranges. As shown in Figure 6, you specify a table of the midpoint value of each range in the histogram and the corresponding count:

{\begin{matrix} x_{1} & c (x_{1}) \\ x_{2} & c (x_{2}) \\ x_{3} & c (x_{3}) \\ . . & . . \\ x_{n} & c (x_{n}) \end{matrix}

As mentioned above, Abaqus/Explicit will renomalize these data to create the piecewise linear probability density function.

Figure 6. Histogram.

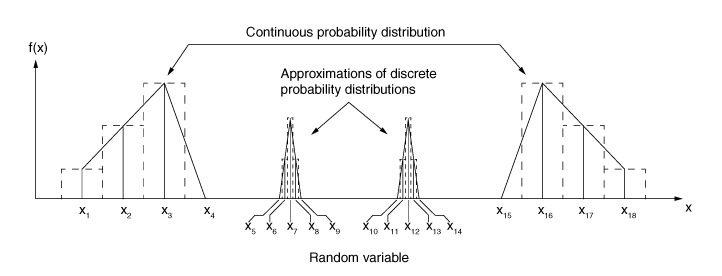
There may be situations where the random variable has continuous values over certain ranges and discrete values elsewhere. Figure 7 shows the use of a piecewise linear probability density function to approximate such distributions where the discrete values are approximated by continuous random variables spanning a very narrow range of values (for example, the discrete value $x_{7}$ is approximated by the continuous range from $x_{5}$ to $x_{9}$ ).

Figure 7. Approximating a discrete probability distribution using a piecewise linear PDF.

Input File Usage

PROBABILITY DENSITY FUNCTION, TYPE=PIECEWISE LINEAR

Discrete probability density function

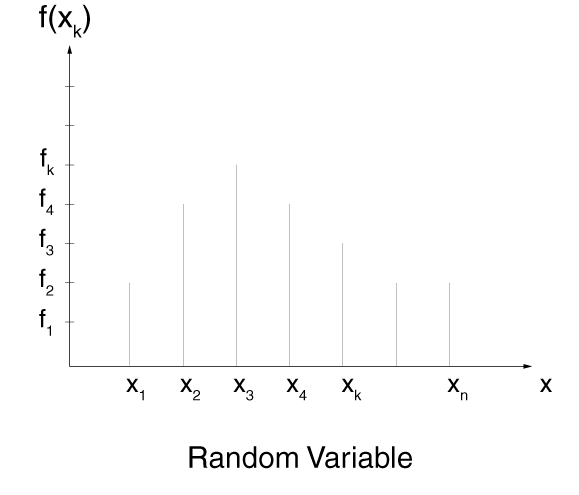
Some applications have only certain specific outcomes. These applications can be represented by a discrete probability density function, as shown in Figure 8. A simple example is throwing of a pair of dice. Only the outcomes of 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12 are possible, with the probabilities of 1/36, 2/36, 3/36, 4/36, 5/36, 6/36, 5/36, 4/36, 3/36, 2/36, and 1/36, respectively. A very specific case of a discrete probability density function is the case when only one value occurs with the probability of 1. To specify a discrete probability density function, you provide a table of the specific values of the random variable along with the corresponding probability:

{\begin{matrix} x_{1} & p_{1} \\ x_{2} & p_{2} \\ x_{3} & p_{3} \\ . . & . . \\ x_{n} & p_{n} \end{matrix}

Abaqus/Explicit will renormalize the specified probabilities to ensure that they sum up to 1.

Input File Usage

PROBABILITY DENSITY FUNCTION, TYPE=DISCRETE

Figure 8. Discrete PDF.

Truncated probability density function

The normal and log-normal probability density functions have open-ended characteristics. These PDFs can be truncated to enforce upper and lower bounds on the value of the random variable. Figure 9 shows a truncated normal distribution $\hat{f} (x)$ where all values of the random variable $x < x_{m i n}$ and $x > x_{m a x}$ from the untruncated normal distribution $f (x)$ have been rejected.

\hat{f} (x) = {\begin{matrix} 0 & x < x_{m i n} \\ \frac{f (x)}{k} & x_{m i n} \leq x \leq x_{m a x} \\ 0 & x > x_{m i n} \end{matrix},

where

k = \int_{x_{m i n}}^{x_{m a x}} f (x) d x .

The factor $k$ represents the probability that the random variable is in the range from $x_{m i n}$ to $x = x_{m a x}$ for the untruncated PDF.

Figure 9. Truncated PDF.

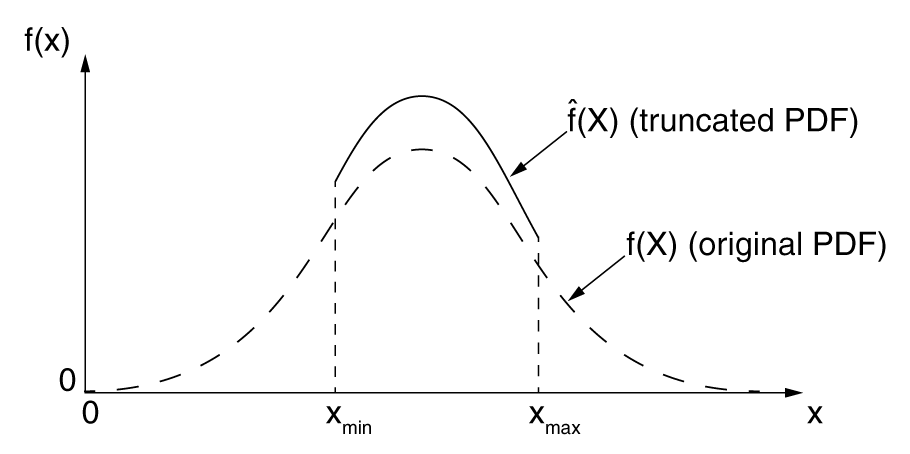
You specify the lower and upper limits of the random variable along with the mean and standard deviation for these types of PDFs. The uniform and the piecewise linear distributions have lower and upper limits for the random variable built into the definition of the PDF and, therefore, do not require renormalization because of truncation.

Output

No output is available for probability density functions.

Limitations

Probability density functions are supported only for the size distributions of PD3D elements created using a particle generator.

Input file template

The following example illustrates the use of a probability density function for particle size distribution:

HEADING
…
PARTICLE GENERATOR, NAME=generator_name, TYPE=PD3D, 
MAXIMUM NUMBER OF PARTICLES=number
**
PARTICLE GENERATOR INLET, SURFACE=inlet_surf
**
PARTICLE GENERATOR MIXTURE
gen_SET1, gen_SET2
**
PROBABILITY DENSITY FUNCTION, NAME=PDF_gen_SET1, TYPE=NORMAL
Data line to define PDF
PROBABILITY DENSITY FUNCTION, NAME=PDF_gen_SET2, TYPE=LOGNORMAL
Data line to define PDF
**
DISCRETE SECTION, ELSET=gen_SET1
PDF_gen_SET1
DISCRETE SECTION, ELSET=gen_SET2
PDF_gen_SET2
…
END STEP

References

Benjamin, J. R., and C. A. Cornell, “Probability, Statistics, and Decision for Civil Engineers,” McGraw-Hill, 1970.
Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, “Numerical Recipes in Fortran 77, The Art of Scientific Computing,” University of Cambridge, 1992.
Saucier, R., “Computer Generation of Statistical Distributions,” Army Research Laboratory, 2000.

Probability density function

Introduction

Applications