About progressive damage and failure

Abaqus offers a general framework for material failure modeling that allows the combination of multiple failure mechanisms acting simultaneously on the same material. Material failure refers to the complete loss of load-carrying capacity that results from progressive degradation of the material stiffness. The stiffness degradation process is modeled using damage mechanics.

To help understand the failure modeling capabilities in Abaqus, consider the response of a typical metal specimen during a simple tensile test. The stress-strain response, such as that illustrated in Figure 1, will show distinct phases. The material response is initially linear elastic, $a-b$, followed by plastic yielding with strain hardening, $b-c$. Beyond point c there is a marked reduction of load-carrying capacity until rupture, $c-d$. The deformation during this last phase is localized in a neck region of the specimen. Point c identifies the material state at the onset of damage, which is referred to as the damage initiation criterion. Beyond this point, the stress-strain response $c-d$ is governed by the evolution of the degradation of the stiffness in the region of strain localization. In the context of damage mechanics $c-d$ can be viewed as the degraded response of the curve $c-d^{\prime }$ that the material would have followed in the absence of damage.

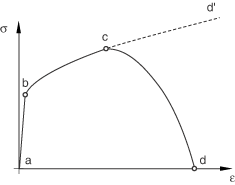
Thus, in Abaqus the specification of a failure mechanism consists of four distinct parts:

• the definition of the effective (or undamaged) material response (e.g., $a-b-c-d^{\prime }$ in Figure 1),

• a damage initiation criterion (e.g., c in Figure 1),

• a damage evolution law (e.g., $c-d$ in Figure 1), and

• a choice of element deletion whereby elements can be removed from the calculations once the material stiffness is fully degraded (e.g., d in Figure 1).

These parts will be discussed separately for ductile metals (About damage and failure for ductile metals) and fiber-reinforced materials (About damage and failure for fiber-reinforced composites).

In continuum mechanics the constitutive model is normally expressed in terms of stress-strain relations. When the material exhibits strain-softening behavior, leading to strain localization, this formulation results in a strong mesh dependency of the finite element results in that the energy dissipated decreases upon mesh refinement. In Abaqus all of the available damage evolution models use a formulation intended to alleviate the mesh dependency. This is accomplished by introducing a characteristic length into the formulation, which in Abaqus is related to the element size, and expressing the softening part of the constitutive law as a stress-displacement relation. In this case the energy dissipated during the damage process is specified per unit area, not per unit volume. This energy is treated as an additional material parameter, and it is used to compute the displacement at which full material damage occurs. This is consistent with the concept of critical energy release rate as a material parameter for fracture mechanics. This formulation ensures that the correct amount of energy is dissipated and greatly alleviates the mesh dependency.