Nonlinear load-displacement curve

The nonlinear load-displacement curve for a structure is shown in Figure 1.

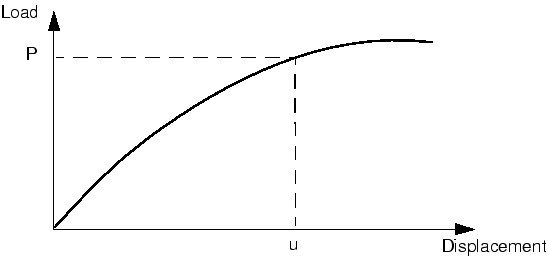
Figure 1. Nonlinear load-displacement curve.

The objective of the analysis is to determine this response. Consider the external forces, P, and the internal (nodal) forces, I, acting on a body (see Figure 2(a) and Figure 2(b), respectively).

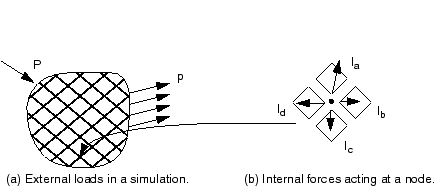
Figure 2. Internal and external loads on a body.

The internal loads acting on a node are caused by the stresses in the elements that contain that node.

For the body to be in static equilibrium, the net force acting at every node must be zero. Therefore, the basic statement of static equilibrium is that the internal forces, I, and the external forces, P, must balance each other:

P - I = 0.

Abaqus/Standard uses the Newton-Raphson method to obtain solutions for nonlinear problems. In a nonlinear analysis the solution usually cannot be calculated by solving a single system of equations, as would be done in a linear problem. Instead, the solution is found by applying the specified loads gradually and incrementally working toward the final solution. Therefore, Abaqus/Standard breaks the simulation into a number of load increments and finds the approximate equilibrium configuration at the end of each load increment. It often takes Abaqus/Standard several iterations to determine an acceptable solution to a given load increment. The sum of all of the incremental responses is the approximate solution for the nonlinear analysis. Thus, Abaqus/Standard combines incremental and iterative procedures for solving nonlinear problems.

Abaqus/Explicit determines a solution to the dynamic equilibrium equation $P - I = M \ddot{u}$ without iterating by explicitly advancing the kinematic state from the end of the previous increment. Solving a problem explicitly does not require the formation of tangent stiffness matrices. The explicit central-difference operator satisfies the dynamic equilibrium equations at the beginning of the increment, t; the accelerations calculated at time t are used to advance the velocity solution to time $t + Δ t / 2$ and the displacement solution to time $t + Δ t$ . For linear and nonlinear problems alike, explicit methods require a small time increment size that depends solely on the highest natural frequency of the model and is independent of the type and duration of loading. Simulations typically require a large number of increments; however, due to the fact that a global set of equations is not solved in each increment, the cost per increment of an explicit method is much smaller than that of an implicit method. The small increments characteristic of an explicit dynamic method make Abaqus/Explicit well suited for nonlinear analysis.