Equilibrium iterations and convergence in Abaqus/Standard

Figure 1. First iteration in an increment.

Convergence

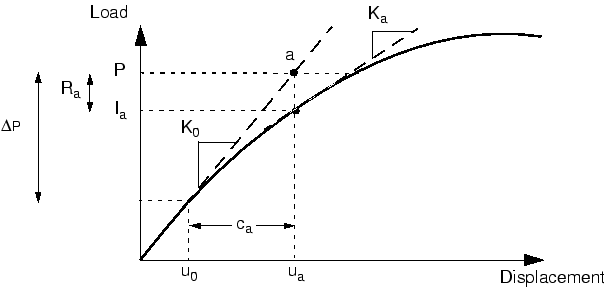
Abaqus/Standard forms a new stiffness, $K_{a}$ , for the structure, based on its updated configuration, $u_{a}$ . Abaqus/Standard also calculates $I_{a}$ , in this updated configuration. The difference between the total applied load, P, and $I_{a}$ can now be calculated as:

R_{a} = P - I_{a},

where $R_{a}$ is the force residual for the iteration.

If $R_{a}$ is zero at every degree of freedom in the model, point a in Figure 1 would lie on the load-deflection curve, and the structure would be in equilibrium. In a nonlinear problem it is almost impossible to have $R_{a}$ equal zero, so Abaqus/Standard compares it to a tolerance value. If $R_{a}$ is less than this force residual tolerance, Abaqus/Standard accepts the structure's updated configuration as the equilibrium solution. By default, this tolerance value is set to 0.5% of an average force in the structure, averaged over time. Abaqus/Standard automatically calculates this spatially and time-averaged force throughout the simulation.

If $R_{a}$ is less than the current tolerance value, P and $I_{a}$ are in equilibrium, and $u_{a}$ is a valid equilibrium configuration for the structure under the applied load. However, before Abaqus/Standard accepts the solution, it also checks that the displacement correction, $c_{a}$ , is small relative to the total incremental displacement, $Δ u_{a} = u_{a} - u_{0}$ . If $c_{a}$ is greater than 1% of the incremental displacement, Abaqus/Standard performs another iteration. Both convergence checks must be satisfied before a solution is said to have converged for that load increment. The exception to this rule is the case of a linear increment, which is defined as any increment in which the largest force residual is less than 10⁻⁸ times the time-averaged force. Any case that passes such a stringent comparison of the largest force residual with the time-averaged force is considered linear and does not require further iteration. The solution is accepted without any check on the size of the displacement correction.

If the solution from an iteration is not converged, Abaqus/Standard performs another iteration to try to bring the internal and external forces into balance. This second iteration uses the stiffness, $K_{a}$ , calculated at the end of the previous iteration together with $R_{a}$ to determine another displacement correction, $c_{b}$ , that brings the system closer to equilibrium (point b in Figure 2).

Figure 2. Second iteration.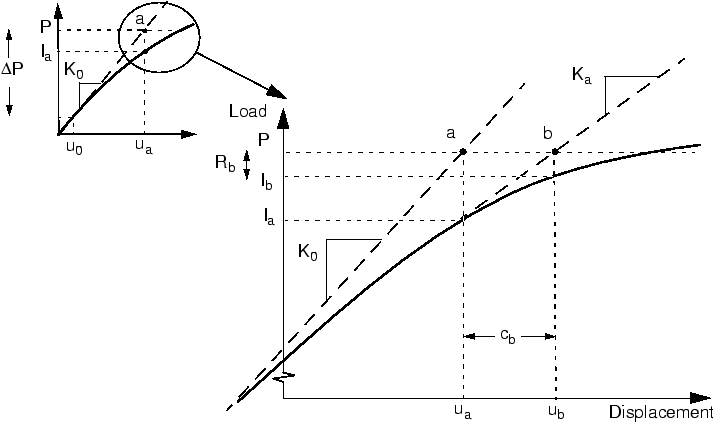

Abaqus/Standard calculates a new force residual, $R_{b}$ , using the internal forces from the structure's new configuration, $u_{b}$ . Again, the largest force residual at any degree of freedom, $R_{b}$ , is compared against the force residual tolerance, and the displacement correction for the second iteration, $c_{b}$ , is compared to the increment of displacement, $Δ u_{b} = u_{b} - u_{0}$ . If necessary, Abaqus/Standard performs further iterations.

For each iteration in a nonlinear analysis Abaqus/Standard forms the model's stiffness matrix and solves a system of equations. This means that each iteration is equivalent, in computational cost, to conducting a complete linear analysis. It should now be clear that the computational expense of a nonlinear analysis in Abaqus/Standard can be many times greater than for a linear one.

It is possible with Abaqus/Standard to save results at each converged increment. Thus, the amount of output data available from a nonlinear simulation is many times that available from a linear analysis of the same geometry. Consider both of these factors and the types of nonlinear simulations that you want to perform when planning your computer resources.