Job monitor and diagnostics | ||
| ||
- Job Monitor
When Abaqus/Standard has finished the simulation, the Job Monitor will contain information similar to that shown in Figure 1.
Figure 1. Job Monitor: perfectly plastic connecting lug.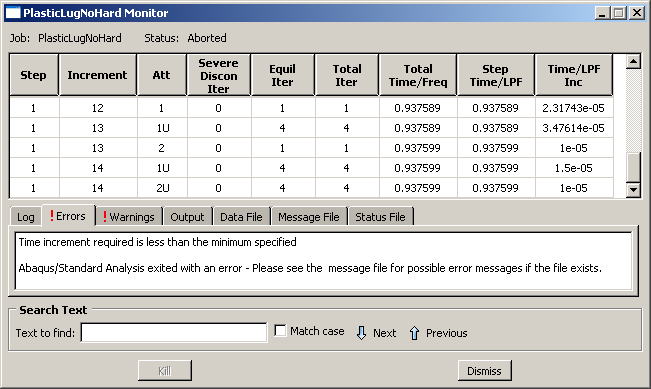
Abaqus/Standard was able to apply only 94% of the prescribed load to the model. The Job Monitor shows that Abaqus/Standard reduced the size of the time increment, shown in the last (right-hand) column, many times during the simulation and stopped the analysis in the fourteenth increment. The information on the Errors tabbed page (see Figure 1) indicates that the analysis terminated. Click the tab to view the error details in the message file, as shown in Figure 2. The error indicates that the analysis terminated because the size of the time increment is smaller than the value allowed for this analysis. This is a classic symptom of convergence difficulties and is a direct result of the continued reduction in the time increment size. To begin diagnosing the problem, click the Warnings tab in the Job Monitor dialog box. As shown in Figure 3, many warning messages concerning large strain increments and problems with the plasticity calculations are found here. These warnings are related since problems with the plasticity calculations are typically the result of excessively large strain increments and often lead to divergence. Thus, we suspect that numerical problems with the plasticity calculations caused Abaqus/Standard to terminate the analysis early.
Figure 2. Message File: error description.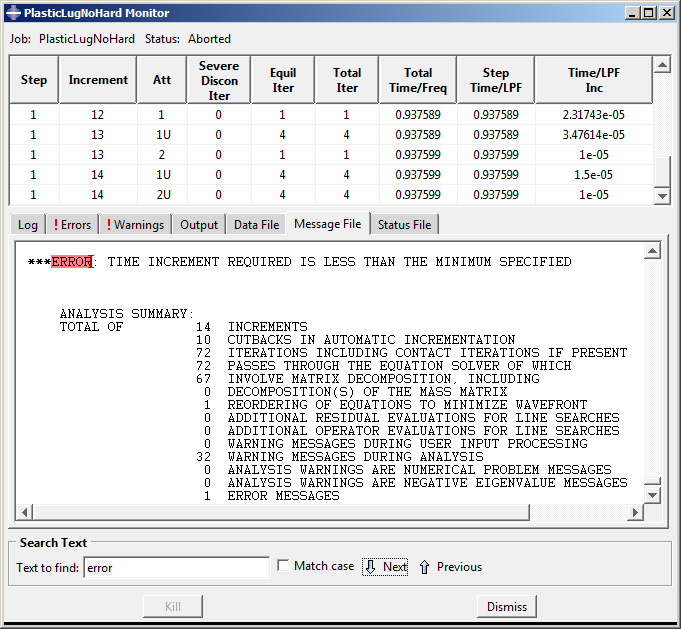 Figure 3. Warnings: perfectly plastic connecting lug.
Figure 3. Warnings: perfectly plastic connecting lug.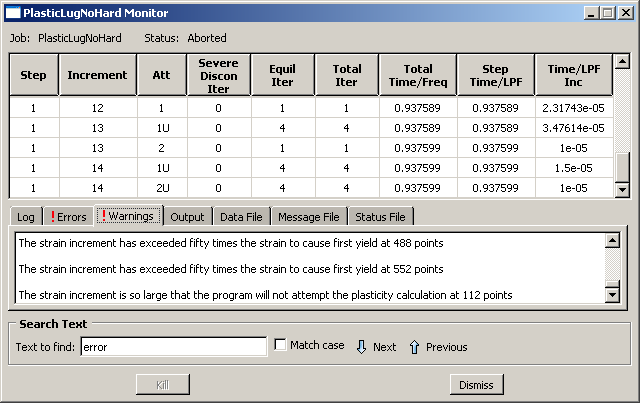
- Job diagnostics
Enter the Visualization module, and open the file PlasticLugNoHard.odb. Open the Job Diagnostics dialog box to examine the convergence history of the job. Looking at the information for the first increment in the analysis (see Figure 4), you will discover that the model's initial behavior is determined to be linear.
Figure 4. Convergence history for Increment 1.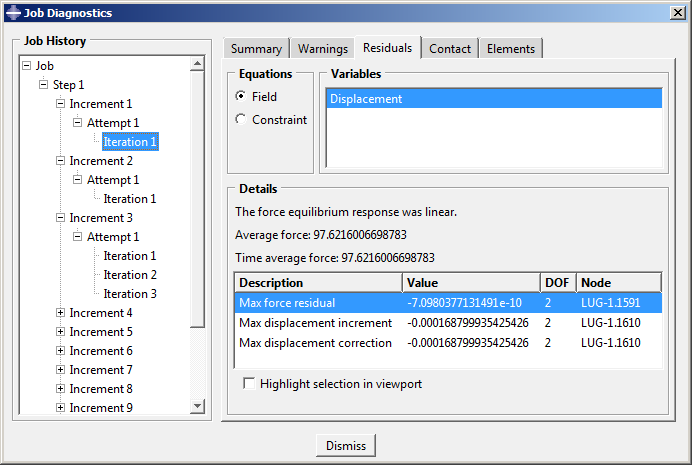
This judgement is based on the fact that the magnitude of the residual, , is less than 10−8 (the time average force); the displacement correction criterion is ignored in this case. The model's behavior is also linear in the second increment (see Figure 5).
Figure 5. Convergence history for Increment 2.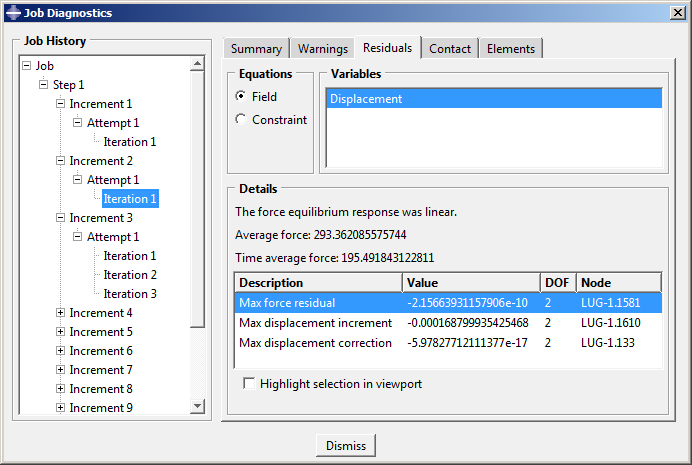
Abaqus/Standard requires several iterations to obtain a converged solution in the third increment, which indicates that nonlinear behavior occurs in the model during this increment. The only nonlinearity in the model is the plastic material behavior, so the steel must have started to yield somewhere in the lug at this applied load magnitude. The summary of the final (converged) iteration for the third increment is shown in Figure 6.
Figure 6. Convergence history for Increment 3.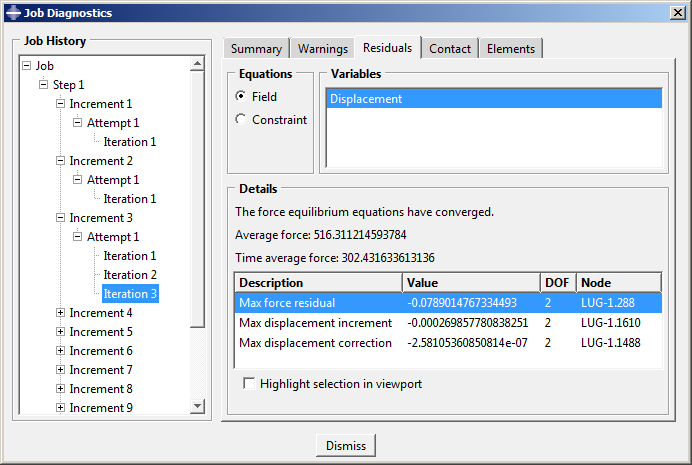
Abaqus/Standard attempts to find a solution in the fourth increment using an increment size of 0.3, which means it is applying 30% of the total load, or 18 kN, during this increment. After several iterations, Abaqus/Standard abandons the attempt and reduces the size of the time increment to 25% of the value used in the first attempt. This reduction in increment size is called a cutback. With the smaller increment size, Abaqus/Standard finds a converged solution in just a few iterations.
Look more closely at the information for the first attempt of the fourth increment (this is where the convergence difficulties first appear). For this attempt Abaqus/Standard detects large strain increments at the integration points of a number of elements, as shown in Figure 7.
Figure 7. Convergence history for Increment 4.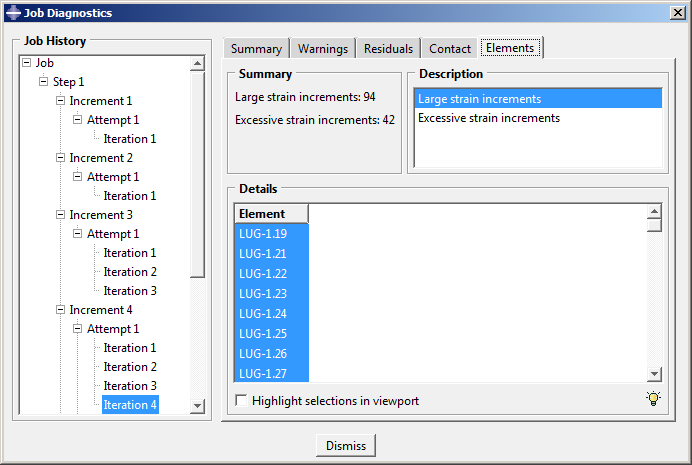
“Large” strain increments are those that exceed the strain at initial yield by 50 times; some of these increments are also considered “excessive,” which implies the plasticity calculations are not even attempted at the affected integration points. Thus, we see that the onset of the convergence difficulties is directly related to the large strain increments and problems with the plasticity calculations.
Abaqus/Standard encounters renewed convergence difficulties in subsequent increments until finally it terminates the job. In many of these increments Abaqus/Standard cuts back the time increment size because the strain increments are so large that the plasticity calculations are not even performed. Thus, we conclude the overall convergence difficulties are indeed the result of numerical problems with the plasticity calculations.
This check on the magnitude of the total strain increment is an example of the many automatic solution controls Abaqus/Standard uses to ensure that the solution obtained for your simulation is both accurate and efficient. The automatic solution controls are suitable for almost all simulations. Therefore, you do not have to worry about providing parameters to control the solution algorithm: you only have to be concerned with the input data for your model.
An interesting observation is made using the Job Diagnostics dialog box: in virtually all attempts where convergence problems are encountered, the elements with large or excessive strain increments are in the vicinity of the built-in end of the lug (where yielding begins) while the node with the largest displacement correction is in the vicinity of the loaded end of the lug. This implies that the loaded end wants to deform more than the built-in end can support. Deformed model shape plots can help you pursue this observation further.