Defining plasticity in Abaqus

Quite often material test data are supplied using values of nominal stress and strain. In such situations you must use the expressions presented below to convert the plastic material data from nominal stress-strain values to true stress-strain values.

The relationship between true strain and nominal strain is established by expressing the nominal strain as

ε_{n o m} = \frac{l - l_{0}}{l_{0}} = \frac{l}{l_{0}} - \frac{l_{0}}{l_{0}} = \frac{l}{l_{0}} - 1.

Adding unity to both sides of this expression and taking the natural log of both sides provides the relationship between the true strain and the nominal strain:

ε = \ln (1 + ε_{n o m}) .

The relationship between true stress and nominal stress is formed by considering the incompressible nature of the plastic deformation and assuming the elasticity is also incompressible, so

l_{0} A_{0} = l A .

The current area is related to the original area by

A = A_{0} \frac{l_{0}}{l} .

Substituting this definition of A into the definition of true stress gives

σ = \frac{F}{A} = \frac{F}{A_{0}} \frac{l}{l_{0}} = σ_{n o m} (\frac{l}{l_{0}}),

where

\frac{l}{l_{0}}

can also be written as

1 + ε_{n o m} .

Making this final substitution provides the relationship between true stress and nominal stress and strain:

σ = σ_{n o m} (1 + ε_{n o m}) .

These relationships are valid only prior to necking.

The classical metal plasticity model in Abaqus defines the post-yield behavior for most metals. Abaqus approximates the smooth stress-strain behavior of the material with a series of straight lines joining the given data points. Any number of points can be used to approximate the actual material behavior; therefore, it is possible to use a very close approximation of the actual material behavior. The plastic data define the true yield stress of the material as a function of true plastic strain. The first piece of data given defines the initial yield stress of the material and, therefore, should have a plastic strain value of zero.

The strains provided in material test data used to define the plastic behavior are not likely to be the plastic strains in the material. Instead, they will probably be the total strains in the material. You must decompose these total strain values into the elastic and plastic strain components. The plastic strain is obtained by subtracting the elastic strain, defined as the value of true stress divided by the Young's modulus, from the value of total strain (see Figure 1).

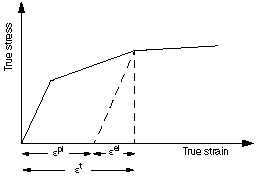
Figure 1. Decomposition of the total strain into elastic and plastic components.

This relationship is written

ε^{p l} = ε^{t} - ε^{e l} = ε^{t} - σ / E,

where

$ε^{p l}$: is true plastic strain,
$ε^{t}$: is true total strain,
$ε^{e l}$: is true elastic strain,
$σ$: is true stress, and
E: is Young's modulus.

Example of converting material test data to Abaqus input

The nominal stress-strain curve in Figure 2 will be used as an example of how to convert the test data defining a material's plastic behavior into the appropriate input format for Abaqus. The six points shown on the nominal stress-strain curve will be used to determine the plastic data.

Figure 2. Elastic-plastic material behavior.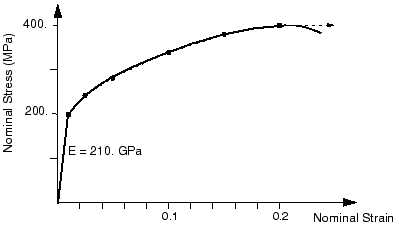

The first step is to use the equations relating the true stress to the nominal stress and strain and the true strain to the nominal strain (shown earlier) to convert the nominal stress and nominal strain to true stress and true strain. Once these values are known, the equation relating the plastic strain to the total and elastic strains (shown earlier) can be used to determine the plastic strains associated with each yield stress value. The converted data are shown in Table 1.

Table 1. Stress and strain conversions.
Nominal Stress (Pa)	Nominal Strain	True Stress (Pa)	True Strain	Plastic Strain
200E6	0.00095	200.2E6	0.00095	0.0
240E6	0.025	246E6	0.0247	0.0235
280E6	0.050	294E6	0.0488	0.0474
340E6	0.100	374E6	0.0953	0.0935
380E6	0.150	437E6	0.1398	0.1377
400E6	0.200	480E6	0.1823	0.1800

While there are few differences between the nominal and true values at small strains, there are very significant differences at larger strain values; therefore, it is extremely important to provide the proper stress-strain data to Abaqus if the strains in the simulation will be large.

Data regularization in Abaqus/Explicit

When performing an analysis, Abaqus/Explicit may not use the material data exactly as defined by the user; for efficiency, all material data that are defined in tabular form are automatically regularized. Material data can be functions of temperature, external fields, and internal state variables, such as plastic strain. For each material point calculation, the state of the material must be determined by interpolation, and, for efficiency, Abaqus/Explicit fits the user-defined curves with curves composed of equally spaced points. These regularized material curves are the material data used during the analysis. It is important to understand the differences that might exist between the regularized material curves used in the analysis and the curves that you specified.

To illustrate the implications of using regularized material data, consider the following two cases. Figure 3 shows a case in which the user has defined data that are not regular.

Figure 3. Example of user data that can be regularized exactly.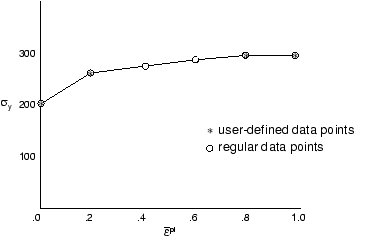

In this example Abaqus/Explicit generates the six regular data points shown, and the user's data are reproduced exactly. Figure 4 shows a case where the user has defined data that are difficult to regularize exactly. In this example it is assumed that Abaqus/Explicit has regularized the data by dividing the range into 10 intervals that do not reproduce the user's data points exactly.

Figure 4. Example of user data that are difficult to regularize.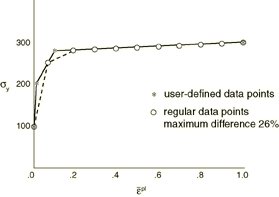

Abaqus/Explicit attempts to use enough intervals such that the maximum error between the regularized data and the user-defined data is less than 3%; however, you can change this error tolerance. If more than 200 intervals are required to obtain an acceptable regularized curve, the analysis stops during the data checking with an error message. In general, the regularization is more difficult if the smallest interval defined by the user is small compared to the range of the independent variable. In Figure 4 the data point for a strain of 1.0 makes the range of strain values large compared to the small intervals defined at low strain levels. Removing this last data point enables the data to be regularized much more easily.

Interpolation between data points

Abaqus interpolates linearly between the data points provided (or, in Abaqus/Explicit, regularized data) to obtain the material's response and assumes that the response is constant outside the range defined by the input data, as shown in Figure 5. Thus, the stress in this material will never exceed 480 MPa; when the stress in the material reaches 480 MPa, the material will deform continuously until the stress is reduced below this value.

Figure 5. Material curve used by Abaqus.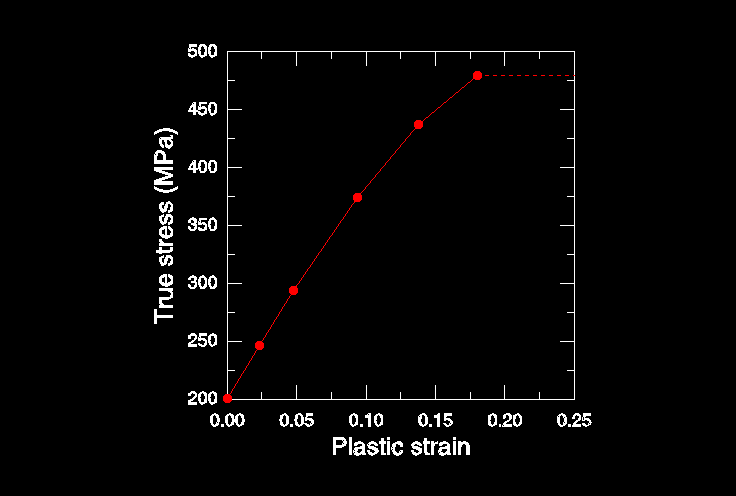

Material calibration in Abaqus/CAE

Abaqus/CAE allows you to calibrate a material model from test data. With this capability, you can import material test data into Abaqus/CAE, process the data, and derive elastic and plastic isotropic material behaviors from the data. This feature is discussed further in Creating material calibrations.