Continuum elements | ||
| ||
Continuum stress/displacement elements in Abaqus have names that begin with the letter “C.” The next two letters indicate the dimensionality and usually, but not always, the active degrees of freedom in the element. The letters “3D” indicate a three-dimensional element; “AX,” an axisymmetric element; “PE,” a plane strain element; and “PS,” a plane stress element.
The use of continuum elements is discussed further in Using Continuum Elements.
- Three-dimensional continuum element library
Three-dimensional continuum elements can be hexahedra (bricks), wedges, or tetrahedra. The full inventory of three-dimensional continuum elements and the nodal connectivity for each type can be found in Three-dimensional solid element library.
Whenever possible, hexahedral elements or second-order tetrahedral elements should be used in Abaqus. First-order tetrahedra (C3D4) have a simple, constant-strain formulation, and very fine meshes are required for an accurate solution.
- Two-dimensional continuum element library
Abaqus has several classes of two-dimensional continuum elements that differ from each other in their out-of-plane behavior. Two-dimensional elements can be quadrilateral or triangular. Figure 1 shows the three classes that are used most commonly.
Figure 1. Plane strain, plane stress, and axisymmetric elements without twist.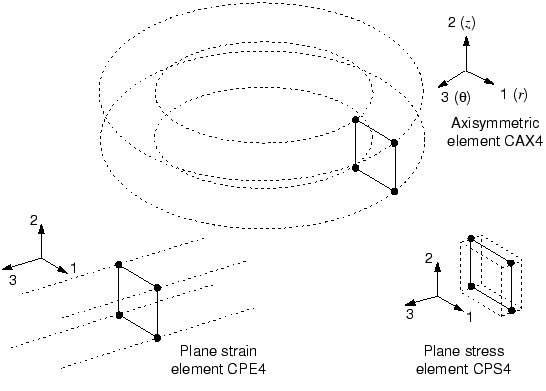
Plane strain elements assume that the out-of-plane strain, , is zero; they can be used to model thick structures.
Plane stress elements assume that the out-of-plane stress, , is zero; they are suitable for modeling thin structures.
Axisymmetric elements without twist, the “CAX” class of elements, model a 360° ring; they are suitable for analyzing structures with axisymmetric geometry subjected to axisymmetric loading.
Abaqus/Standard also provides generalized plane strain elements, axisymmetric elements with twist, and axisymmetric elements with asymmetric deformation.
Generalized plane strain elements include the additional generalization that the out-of-plane strain may vary linearly with position in the plane of the model. This formulation is particularly suited for the thermal-stress analysis of thick sections.
Axisymmetric elements with twist model an initially axisymmetric geometry that can twist about the axis of symmetry. These elements are useful for modeling the torsion of cylindrical structures, such as axisymmetric rubber bushings.
Axisymmetric elements with asymmetric deformation model an initially axisymmetric geometry that can deform asymmetrically (typically as a result of bending). They are useful for simulating problems such as an axisymmetric rubber mount that is subjected to shear loads.
The latter three classes of two-dimensional continuum elements are not discussed in this guide.
Two-dimensional solid elements must be defined in the 1–2 plane so that the node order is counterclockwise around the element perimeter, as shown in Figure 2.
Figure 2. Correct nodal connectivity for two-dimensional elements.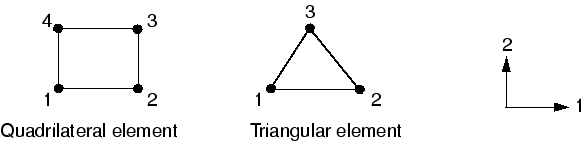
When using a preprocessor to generate the mesh, ensure that the element normals all point in the same direction as the positive, global 3-axis. Failure to provide the correct element connectivity will cause Abaqus to issue an error message stating that elements have negative area.
- Degrees of freedom
All of the stress/displacement continuum elements have translational degrees of freedom at each node. Correspondingly, degrees of freedom 1, 2, and 3 are active in three-dimensional elements, while only degrees of freedom 1 and 2 are active in plane strain elements, plane stress elements, and axisymmetric elements without twist. To find the active degrees of freedom in the other classes of two-dimensional solid elements, see Two-dimensional solid element library.
- Element properties
All solid elements must refer to a solid section property that defines the material and any additional geometric data associated with the element. For three-dimensional and axisymmetric elements no additional geometric information is required: the nodal coordinates completely define the element geometry. For plane stress and plane strain elements the thickness of the elements may be specified or a default value of 1 will be used.
- Formulation and integration
Alternative formulations available for the continuum family of elements in Abaqus/Standard include an incompatible mode formulation (the last or second-to-last letter in the element name is I) and a hybrid element formulation (the last letter in the element name is H), both of which are discussed in detail later in this guide.
In Abaqus/Standard you can choose between full and reduced integration for quadrilateral and hexahedral (brick) elements. In Abaqus/Explicit you can choose between full and reduced integration for hexahedral (brick) elements; however, only reduced integration is available for quadrilateral first-order elements. Both the formulation and type of integration can have a significant effect on the accuracy of solid elements, as discussed in Element formulation and integration.
- Element output variables
By default, element output variables such as stress and strain refer to the global Cartesian coordinate system. Thus, the -component of stress at the integration point shown in Figure 3(a) acts in the global 1-direction. Even if the element rotates during a large-displacement simulation, as shown in Figure 3(b), the default is still to use the global Cartesian system as the basis for defining the element variables.
Figure 3. Default material directions for continuum elements.
However, Abaqus allows you to define a local coordinate system for element variables (see Example: skew plate). This local coordinate system rotates with the motion of the element in large-displacement simulations. A local coordinate system can be very useful if the object being modeled has some natural material orientation, such as the fiber directions in a composite material.