Troubleshooting Abaqus/Standard contact analyses | ||
| ||
If a contact analysis runs into difficulty, the first thing to check is whether the contact surfaces are defined correctly. The easiest way to do this is to run a datacheck analysis and plot the surface normals in the Visualization module. You can plot all of the normals, for both surfaces and structural elements, on either the deformed or the undeformed plots. Use the Normals options in the Common Plot Options dialog box to do this, and confirm that the surface normals are in the correct directions.
Abaqus/Standard may still have some problems with contact simulations, even when the contact surfaces are all defined correctly. One reason for these problems may be the default convergence tolerances and limits on the number of iterations: they are quite rigorous. In contact analyses it is sometimes better to allow Abaqus/Standard to iterate a few more times rather than abandon the increment and try again. This is why Abaqus/Standard makes the distinction between severe discontinuity iterations and equilibrium iterations during the simulation.
The diagnostic contact information is essential for almost every contact analysis. This information can be vital for spotting mistakes or problems. For example, chattering can be spotted because the same slave node will be seen to be involved in all of the severe discontinuity iterations. If you see this, you will have to modify the mesh in the region around that node or add constraints to the model. Contact diagnostic information can also identify regions where only a single slave node is interacting with a surface. This is a very unstable situation and can cause convergence problems. Again, you should modify the model to increase the number of elements in such regions.
- Contact diagnostics
To illustrate how to interpret the contact diagnostic information in Abaqus/CAE, consider the iterations in the seventh increment of the second step. This increment is one in which severe discontinuity iterations are required. Abaqus/Standard requires three iterations to establish the correct contact conditions in the model; i.e., whether or not the punch was contacting the blank. The fourth and fifth iterations do not produce any changes in the model's contact state but do not achieve equilibrium. One additional iteration is required to converge on static equilibrium. Thus, once Abaqus/Standard determines the correct contact state, it can easily find the equilibrium solution.
To further investigate the behavior of the model in this increment, look at the visual diagnostic information available in Abaqus/CAE. The diagnostic information written to the output database file provides detailed information about the changes in the model's contact conditions. For example, the node number and location in the model of every slave node whose contact status changes in a severe discontinuity iteration, as well as the contact interaction to which it belongs, can be obtained using the visual diagnostics tool.
Enter the Visualization module, and open the file Channel.odb to look at the contact diagnostics information. In the first severe discontinuity iteration of the second step (increment 7, attempt 1), four nodes on the blank experience contact openings, indicating that their assumed contact state is incompatible. This incompatibility can be seen in the Contact tabbed page of the Job Diagnostics dialog box (see Figure 1). To see where the nodes are located on the model, toggle on Highlight selections in viewport.
Figure 1. Contact openings in the first severe discontinuity iteration.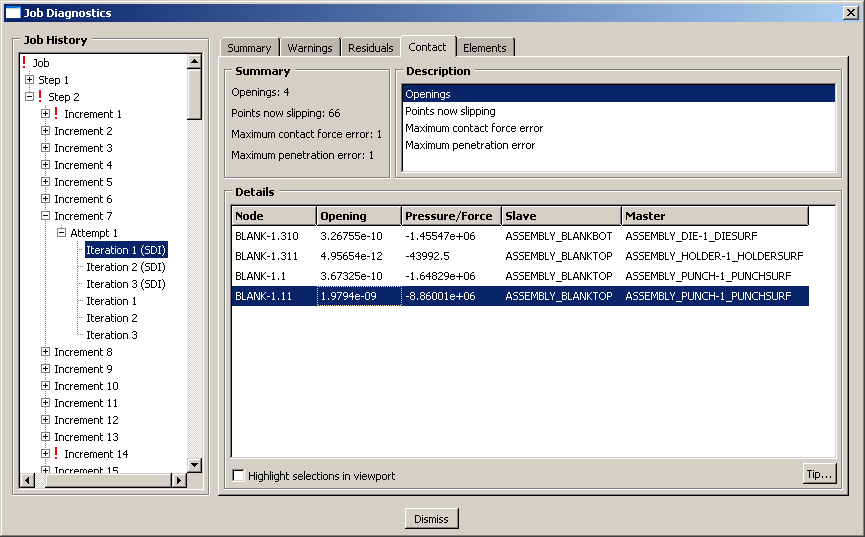
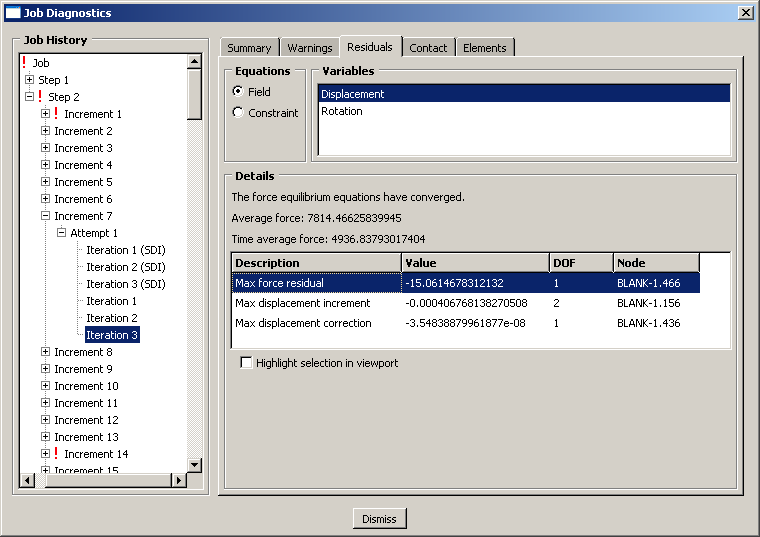
Since neither the contact state nor the equilibrium checks pass in this iteration, Abaqus/Standard removes the contact constraints from these nodes and performs another iteration. After two additional iterations Abaqus/Standard detects no changes in the contact state. The solution in the fourth and fifth iterations do not satisfy the force residual tolerance check, so another iteration is performed. This time, not only is the contact state converged, but the force residual tolerance check is satisfied and the displacement correction is acceptable relative to the largest displacement increment, as shown in Figure 2. Thus, the third equilibrium iteration produces a converged solution for this increment.
Figure 2. Converged equilibrium iteration.