Friction models

The default friction coefficient is zero. The tangential motion is zero until the surface traction reaches a critical shear stress value, which depends on the normal contact pressure, according to the following equation:

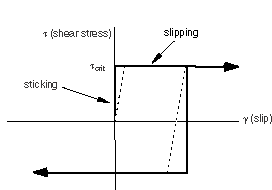
where $\mu$ is the coefficient of friction and $p$ is the contact pressure between the two surfaces. This equation gives the limiting frictional shear stress for the contacting surfaces. The contacting surfaces will not slip (slide relative to each other) until the shear stress across their interface equals the limiting frictional shear stress, $\mu p$. For most surfaces $\mu$ is normally less than unity. Coulomb friction can be defined with $\mu$ or ${\tau }_{\mathrm{crit}}$. The solid line in Figure 1 summarizes the behavior of the Coulomb friction model: there is zero relative motion (slip) of the surfaces when they are sticking (the shear stresses are below $\mu p$). Optionally, a friction stress limit can be specified if both contacting surfaces are element-based surfaces.

In Abaqus/Standard the discontinuity between the two states—sticking or slipping—can result in convergence problems during the simulation. You should include friction in your Abaqus/Standard simulations only when it has a significant influence on the response of the model. If your contact simulation with friction encounters convergence problems, one of the first modifications you should try in diagnosing the difficulty is to rerun the analysis without friction. In general, friction presents no additional computational difficulties for Abaqus/Explicit.

Simulating ideal friction behavior can be very difficult; therefore, by default in most cases, Abaqus uses a penalty friction formulation with an allowable “elastic slip,” shown by the dotted line in Figure 1. The “elastic slip” is the small amount of relative motion between the surfaces that occurs when the surfaces should be sticking. Abaqus automatically chooses the penalty stiffness (the slope of the dotted line) so that this allowable “elastic slip” is a very small fraction of the characteristic element length. The penalty friction formulation works well for most problems, including most metal forming applications.

In those problems where the ideal stick-slip frictional behavior must be included, the “Lagrange” friction formulation can be used in Abaqus/Standard and the kinematic friction formulation can be used in Abaqus/Explicit. The “Lagrange” friction formulation is more expensive in terms of the computer resources used because Abaqus/Standard uses additional variables for each surface node with frictional contact. In addition, the solution converges more slowly so that additional iterations are usually required. This friction formulation is not discussed in this guide.

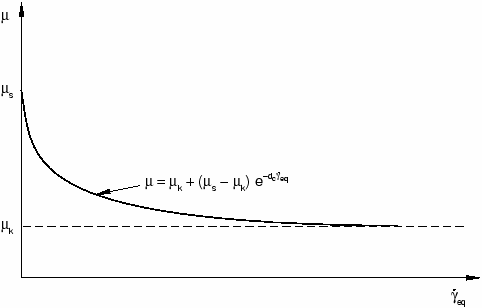
Often the friction coefficient at the initiation of slipping from a sticking condition is different from the friction coefficient during established sliding. The former is typically referred to as the static friction coefficient, and the latter is referred to as the kinetic friction coefficient. In Abaqus an exponential decay law is available to model the transition between static and kinetic friction (see Figure 2). This friction formulation is not discussed in this guide.

In Abaqus/Standard the inclusion of friction in a model adds unsymmetric terms to the system of equations being solved. If $\mu$ is less than about 0.2, the magnitude and influence of these terms are quite small and the regular, symmetric solver works well (unless the contact surface has high curvature). For higher coefficients of friction, the unsymmetric solver is invoked automatically because it will improve the convergence rate. The unsymmetric solver requires twice as much computer memory and scratch disk space as the symmetric solver. Large values of $\mu$ generally do not cause any difficulties in Abaqus/Explicit.